
Практикум по коллоидной химии 1 семестр
.pdfМосковская Государственная Академия Тонкой Химической Технологии
им. М.В.Ломоносова (МГАТХТ), 1999 г.
Учебно-методическое пособие
Буканова Е.Ф., Григорьев Г.А., Дулина О.А.
(под редакцией проф. Туторского И.А.)
Практикум по коллоидной химии
“Поверхностные явления и адсорбция”.
(для студентов бакалавриата)
www.mitht.ru/e-library

Сдано в печать. Формат 60*90.16 Печать офсетн.
Бумага офсетн. Усл.изд.л. 1,5. Тираж 500 экз. Заказ №
Москва, пр. Вернадского-86 Издательско-полиграфический центр МГАТХТ
им. М.В. Ломоносова
Оглавление
1.Введение
2.Лабораторные работы
Работа 1. |
Измерение поверхностного натяжения сталагмо- |
|||
|
метрическим методом, методом отрыва кольца |
|||
|
или методом максимального давления в газовом |
|||
|
пузырьке или капле. |
|
|
|
Работа 2. |
Определение термодинамических свойств меж- |
|||
|
фазного слоя. |
|
|
|
Работа 3. |
Исследование взаимосвязи между поверхностным |
|||
|
натяжением и адсорбцией. |
|
|
|
Работа 4. |
Исследование |
влияния |
длины |
радикала |
|
поверхностно-активных веществ на их поверхно- |
|||
|
стную активность. Определение параметров ад- |
|||
|
сорбционного слоя. |
|
|
|
Работа 5. |
Исследование влияния поверхностно-активных |
|||
|
веществ на смачивание и адгезию. |
|
||
Работа 6. |
Определение удельной поверхности адсорбента. |
|||
Работа 7. |
Исследование адсорбции из растворов. |
|
||
Работа 8. |
Исследование адсорбции красителя из раствора |
|||
|
на ткани. |
|
|
|
Работа 9. |
Исследование кинетики адсорбции. |
|
||
.
www.mitht.ru/e-library

1. Введение
Коллоидные системы - это высокодисперсные гетерогенные системы с сильно развитой поверхностью раздела фаз. Молекулы поверхностного слоя дисперсной фазы граничат не только с себе подобными, но и с молекулами окружающей ее дисперсионной среды . Поэтому равнодействующая молекулярных сил в поверхностном слое не равна нулю. Различие в свойствах молекул на границе раздела и в объеме фаз приводит к тому, что поверхностные молекулы будут втягиваться вглубь фазы, что в свою очередь вызывает натяжение вдоль поверхности раздела фаз, называемое поверхностным или межфазным натяжением . Натяжение на границе конденсированной и газовой фазы обычно называют поверхностным натяжением, а между двумя конденсированными фазами - межфазным натяжением. Для увеличения поверхности раздела фаз необходим перенос некоторого количества молекул из объема в поверхностный слой. Поэтому поверхностное натяжение можно характеризовать величиной изотермической обратимой работы, необходимой для преодоления межмолекулярного сцепления при увеличении поверхности раздела. Производимая над системой работа в этом случае приводит к увеличению свободной поверхностной энергии FS . Свободная поверхностная энергия FS определяется произведением поверхностного натяжения на площадь поверхности S :
FS S |
(1.1) |
|||
Связь между удельной поверхностью Sуд., поверхностью S, объемом V, и |
||||
дисперсностью D выражается соотношением : |
|
|||
S |
|
S |
k D |
(1.2) |
|
||||
уд |
|
V |
|
|
где K - коэффициент формы частиц, для сферических частиц равный 6. Поверхностное натяжение можно выразить частной производной от любого термодинамического потенциала по величине межфазной поверхности при постоянных соответствующих параметрах :
F I |
F I |
F I |
F I |
|
||||
U |
H |
F |
G |
|
||||
G |
J |
G |
J |
G |
J |
G |
J |
(1.3) |
HSKS,V,ni |
HSKSP,,ni |
HSKT,V,ni |
HSKT,P,ni |
|
||||
Термин “натяжение”, возникший исторически в связи с гипотезой упругой пленки, выражает представление о величине как о силе, действующей по касательной к поверхности жидкости и стремящейся ее сократить. Исходя из такого представления можно сказать, что поверхностное натяжение - это сила, действующая на 1м длины контура поверхности. Очевидно, что оба способа выражения как энергии (работы) и как силы -эквивалентны относительно единиц измерения. Размерность
|
|
|
Дж |
или |
Н |
|
, т.к. Дж Н м |
|
|||||||
|
2 |
м |
|||||
|
|
|
м |
|
|
||
Высокодисперсные, например, коллоидные системы обладают избыточной свободной энергией, уменьшение которой происходит согласно второму закону термодинамики, при протекании самопроизвольных процессов.
www.mitht.ru/e-library
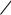
При этом уменьшение свободной поверхностной энергии происходит как за счет уменьшения величины поверхности раздела фаз S, так и самого поверхностного натяжения .
Уменьшение поверхностной энергии при коагуляции или коалесценции связано с уменьшением величины поверхности раздела фаз, уменьшение происходит при перераспределении компонентов между поверхностным слоем и объемом граничащих фаз.
В природе наблюдается много процессов, которые связаны с уменьшением поверхностного натяжения. В коллоидной химии - это образование коагуляционных или конденсационных структур, стабилизация коллоидных систем, смачивание, адсорбция , образование зародышей при кристаллизации и многое другое.
Явления связанные с особенностями поверхности раздела, называются поверхностными явлениями. Вклад свойств межфазного слоя в общие термодинамические свойства гетерогенной системы в настоящее время может быть учтен двумя методами :
1.Методом избыточных величин Гиббса
2.Методом слоев конечной толщины
Чаще всего для плоской границы раздела между фазами используется первый метод. Сущность метода заключается в том , что Гиббс вычитает из общетермодинамических свойств гетерогенной системы термодинамические свойства граничащих фаз, а полученные избытки относит к единице поверхности проведенной внутри поверхностного слоя, которую он назвал разделяющей.
Эти избытки могут быть определены на основании фундаментальных уравнений для межфазного слоя:
dUS T dSS dS i dniS |
(1.4) |
i |
|
На основе фундаментальных термодинамических соотношенй выводится и адсорбционное уравнение Гиббса:
|
|
|
d Гi d i |
(1.5) |
|
|
|
i |
|
|
|
nS |
|
|
где Гi |
|
i |
- обычно называется Гиббсовской адсорбцией . |
|
|
|
|||
|
|
S |
|
|
Адсорбция - это процесс выравнивания химического потенциала, приводящий к перераспределению компонентов между объемом и поверхностью фаз. Вещество, на котором адсорбируются компоненты, называют адсорбентом, а адсорбирующиеся компоненты - адсорбатом. По характеру взаимодействия адсорбата с адсорбентом (природе сил) различают физическую и химическую адсорбции. Чаще всего при анализе адсорбции рассматривают изотермы, которые лежат в основе исторически сложившихся теорий адсорбции.
Изотерма Бедеккера-Фрейндлиха описывается уравнением:
1 |
(1.6) |
A c n |
где и n - эмпирические константы
www.mitht.ru/e-library

с - концентрация компонента.
Изотерма, вытекающая из теории мономолекулярной адсорбции Лен-
гмюра, описывается выражением : |
Amax k c |
|
|
|
|
A |
|
|
(1.7) |
||
1 k c |
|||||
|
|
||||
где Амах- максимальная адсорбция при заполнении на поверхности ад- |
|||||
сорбента монослоя |
|
|
kадс |
|
|
к- константа адсорбционного равновесия k |
, |
||||
kдес |
|||||
|
|
|
|
||
где кадс - константа скорости адсорбции, кдес - константа скорости десорбции.
Уравнение изотермы полимолекулярной адсорбции Брунауэра, Эммета, Теллера (БЭТ) имеет вид:
A |
max |
c p |
|
|
||||
|
ps |
|
|
|||||
A d1 pps i |
|
1 bc 1gpps |
|
|
|
(1.8) |
||
|
|
|
||||||
где с - константа адсорбционного равновесия, р - давление пара компонента,
рs - давление насыщенного пара того же компонента.
Несмотря на то, что с термодинамической точки зрения процессы адсорбции на разных межфазных границах не отличаются друг от друга, условно различают следующие виды адсорбции: на границе твердое - газ или пар; жидкость - газ или пар; твердое тело - жидкость. Последний вид адсорбции называют адсорбцией из растворов.
Адсорбция на границе твердое - газ описывается обычно теорией мономолекулярной адсорбции Ленгмюра для газов или теорией полимолекулярной адсорбции БЭТ в случае паров. Для межфазной границы жидкость - газ или пар используется уравнение изотермы Гиббса. Это уравнение при определенном выборе положения разделяющей поверхности в межфазном слое, позволяет по изменению поверхностного натяжения рассчитать величину адсорбции компонентов раствора на этой поверхности. В случае разбавленных растворов, близких к идеальным, уравнение для адсорбции имеет вид:
Г |
c |
|
d |
(1.9) |
|
dc |
|||
R T |
|
|
||
где с - концентрация, моль/л;
R - универсальная газовая постоянная; T - абсолютная температура
В этом уравнении величина q FGd IJ называется поверхностной ак-
HdcKc 0
тивностью и является мерой способности вещества понижать поверхност-
ное натяжение на границе раздела фаз. Знак производной d и опредеdc
ляет поверхностную активность компонента. Для d <0, как следует из dc
www.mitht.ru/e-library

уравнения, Г>0 и такой компонент называют поверхностно-активным веще-
ством (ПАВ). В случае, когда d >0 , Г<0 компонент называют поверхностdc
но-инактивным (ПИВ).
Расчет Г осуществляется на основе экспериментальной зависимостиfbc методом графического дифференцирования или по уравнению
Шишковского; имеющего вид : |
|
0 Amax R T lnb1 k c |
(1.10) |
где 0 - поверхностное натяжение чистого растворителя ; c - концентрация ПАВ
Адсорбция из растворов на поверхности твердого тела зависит от взаимодействия адсорбента и среды, которое определяется явлениями смачивания, растекания, адгезии и когезии.
Когезия - это сцепление в объеме однородного тела. Работа когезии Wk - это обратимая изотермическая работа разделения столбика вещества с площадью поперечного сечения, равной 1. Согласно этому определению:
Wk 2 жг (1.11)
Работа адгезии WА - это обратимая изотермическая работа разделения двух разнородных конденсированных фаз вдоль межфазной поверхности, равной 1.
Согласно закону Дюпре:
WА = тг + жг - тж |
(1.12) |
Из уравнения Дюпре следует, что чем больше работа адгезии, тем меньше межфазное натяжение тж .
Смачивание характеризуется краевым углом смачивания . Согласно
закону Юнга: |
|
||
cos |
тг тж |
(1.13) |
|
жг |
|||
|
|
||
Совместное уравнение Дюпре-Юнга, позволяет по экспериментально определенному cos рассчитать работу адгезии:
WА = жг (1+ cos ) |
(1.14) |
Условия самопроизвольного смачивания или растекания определяются |
|
коэффициентом растекания по Гаркинсу f: |
|
f = тг - тж - жг или f = WA - WK |
(1.15) |
www.mitht.ru/e-library
2. ЛАБОРАТОРНЫЕ РАБОТЫ
РАБОТА 1.
ИЗМЕРЕНИЕ ПОВЕРХНОСТНОГО НАТЯЖЕНИЯ СТАЛАГМОМЕТРИЧЕСКИМ МЕТОДОМ, МЕТОДОМ ОТРЫВА КОЛЬЦА ИЛИ МЕТОДОМ МАКСИМАЛЬНОГО ДАВЛЕНИЯ В ГАЗОВОМ
ПУЗЫРЬКЕ ИЛИ КАПЛЕ
Цель работы
Ознакомление с методами измерения поверхностного натяжения. Сопоставление изотерм поверхностного натяжения поверхностноактивных веществ и поверхностно-инактивпых веществ.
Теоретическая часть
Поверхностное натяжение можно измерять непосредственно только в условиях обратимого изменения поверхности раздела фаз, т. е. при достаточной подвижности этой поверхности, например на границах жидкость - пар иди жидкость - жидкость при не слишком высокой вязкости жидкостей. Поверхностное натяжение твердых тел определяется с большими трудностями и, как правило, косвенными методами.
Методы измерения поверхностного натяжения подразделяются на статические или полустатические (при неподвижных или медленно образующихся поверхностях раздела) и динамические (при движущихся и непрерывно обновляющихся поверхностях раздела).
Динамические методы сложны и, кроме того, они не применимы для измерения поверхностного натяжения растворов поверхностно-активных веществ (ПАВ), так как время формирования адсорбционных слоев часто довольно значительно, и тогда поверхностное натяжение, измеренное за малые промежутки времени существования поверхности, не будет соответствовать равновесному значению .
Статические или полустатическис методы позволяют измерять равновесные значения поверхностного натяжения. Наиболее распространенными из них являются методы капиллярного поднятия, максимального давления в пузырьках и каплях, сталагмометрический (отрывающейся капли) и отрыва кольца. Последние три метода позволяют определять не только поверхностное натяжение, но и межфазное натяжение на границе двух несмешивающихся жидкостей.
Измерение поверхностного натяжения сталагмометрическим мето-
дом основано на том, что в момент отрыва капли от нижнего конца вертикальной трубки вес капли q уравновешивается силой поверхностного натяжения F (см. рис. 2.1), которая действует вдоль окружности шейки капли и препятствует ее отрыву. В первом приближении можно считать, что
www.mitht.ru/e-library
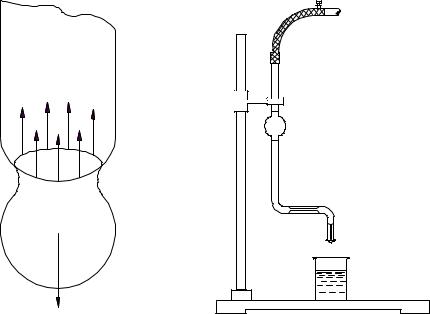
F 2 r |
(2.1) |
где r - внутренний радиус трубки.
F
q
Рис. 2.1. Схема отрыва капли |
Рис. 2.2. Сталагмометр. |
от конца капиллярной трубки. |
|
При более точном определении следует учитывать, что разрыв происходит в щейке капли, которая имеет меньший радиус, чем трубка. Поэтому значение радиуса r надо умножить на некоторый коэффициент k , зависящий от отношения объема капли к кубу радиуса трубки, k fd/r3i
Экспериментально показано, что этот коэффициент не очень сильно меняется при изменении объема капель даже в 1000 раз. Для капель, сравнительно мало отличающихся по объему, этот коэффициент можно считать одинаковым. Так как в момент отрыва F = q , то, определив вес образующейся капли q , можно вычислить поверхностное натяжение жидкости . Для определения веса капли пользуются сталагмометром, который представляет собой стеклянную трубку с расширением посредине, заканчивающуюся внизу капилляром (рис. 2.2). Трубка обычно имеет горизонтальную коленчатую часть, в которую впаян капилляр для того, чтобы жидкость капала медленнее. Расширенная часть трубки ограничена двумя метками. Для измерения поверхностного натяжения в сталагмометр засасывают исследуемую жидкость выше верхней метки; когда уровень жидкости опустится до верхней метки, начинают считать число капель n жидкости,
вытекающей из трубки, до тех пор, пока уровень жидкости не достигнет нижней метки. Если известны объем расширенной части сталагмометра V и плотность жидкости , то вес капли q можпо вычислить по формуле
q |
V g |
(2.2) |
|
n |
|||
|
|
www.mitht.ru/e-library
где g - ускорение силы тяжести. |
|
|||
Очевидно, что при отрыве капли должно соблюдаться равенство |
|
|||
2 r |
V g |
|
(2.3) |
|
n |
||||
|
|
|||
Обычно проводят относительное определение , сравнивая истечение из данного сталагмометра исследуемой жидкости и жидкости с известным поверхностным натяжением. В этом случае, написав уравнение (2.3) для обеих жидкостей, разделив первое из этих уравнений на второе и сократив постоянные величины, получают формулу для расчета:
x |
|
x |
|
nст |
или |
|
|
|
x |
|
nст |
(2.4) |
||||
|
|
|
x |
ст |
|
|||||||||||
|
ст |
|
|
ст |
|
n |
x |
|
|
|
n |
x |
|
|||
|
|
|
|
|
|
|
|
|
ст |
|
|
|
||||
В этих уравнениях индекс x относится к параметрам исследуемой жидкости, а индекс
ст - к параметрам жидкости с известным поверхностным натяжением.
Если стандартной жидкостью является вода, величину ncт называют «водяным числом» сталагмометра. Значение ст для воды при 200 С равно
72,7 мДж/м2.
При измерении сталагмометром поверхностного натяжения растворов эмульгаторов, смачивателей и моющих средств, имеющих большие молекулы, необходимо увеличивать время образования капли. В противном случае, если капля образуется быстро, на ее поверхности из-за медленной диффузии таких молекул не успевает установиться равновесное значение поверхностного натяжения. Для подобных растворов измерения проводят при различных, все уменьшающихся скоростях истечения, пока число капель n , не приобретет максимальное постоянное значение. Это значение и берут для расчета.
Для увеличения времени образования капли в простейшем случае пользуются винтовым зажимом, позволяющим изменять просвет каучуковой трубки (рис. 2.4) и тем самым уменьшать скорость истечения .
При правильно выбранном времени образования капель сталагмометрический метод дает достаточно точные значения поверхностного натяжения растворов ПАВ.
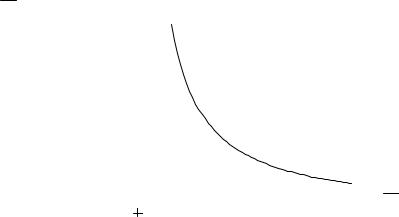
К недостаткам этого метода следует отнести неопределенность, связанную с тем, что в процессе отрыва капли часть жидкости остается на кончике капилляра. Чтобы учесть эту поправку, можно воспользоваться таблицами или графиком, передающим зависимость поправочного коэффициента от
безразмерного критерия H .
FGIJ
r3 k
Рис. 2.2.Графическое определение поправочного коэффициента k в сталагмометрическом методе.
r3
www.mitht.ru/e-library
Эта поправка может составлять 25-40 %, поэтому для определения абсолютного значения поверхностного натяжения метод не дает надежных результатов. Чаще всего его используют в относительном варианте, т.е. измеряют поверхностное натяжение жидкости, сравнивая его с жидкостью с известным поверхностным натяжением. Кроме того результаты измерений даже в относительном варианте зависят от смачивания материала капилляра данной жидкостью. Жидкости разной природы могут по разному смачивать капилляр. Смачивание изменяется с изменением концентрации второго компонента, например, ПАВ. Для того чтобы уменьшить эту неопределенность, торец капилляра должен быть тщательно отполирован и заточен “на нож” , т.е., на нулевую толщину стенки торца.
Определение поверхностного натяжения методом отрыва кольца
(с помощью тензиометра) заключается в измерении силы, необходимой для отрыва проволочного кольца вместе со смачивающей его жидкостью от поверхности жидкости. Необходимым условием при использовании этого метода является полное смачивание кольца жидкостью.
При поднятии кольца с помощью приложенной внешней силы F кольцо вытягивает за собой столбик жидкости объемом , вес Q которого всегда равен значению приложенной силы. Благодаря поверхностному натяжению этот столбик удерживается от разрыва. Сила поверхностного натяжения F , стремящаяся сократить поверхность столбика жидкости, равна произведению значения поверхностного натяжения на сумму внутреннего и внешнего периметров кольца:
F 2 R1 2 bR1 2rg 4 R |
(2.5) |
где R1 - внутренний радиус кольца; r - радиус сечения проволоки; R - среднее арифметическое значение внутреннего и внешнего радиусов кольца.
Когда силы, действующие на столбик жидкости (F и Q), достигнут значения силы поверхностного натяжения F ,столбик разрывается и кольцо вместе с прилипшей к нему жидкостью отрывается от поверхности исследуемого раствора. В момент отрыва кольца
F Q g F 4 R |
(2.6) |
где - плотность жидкости; g - ускорение силы тяжести.
При этом предполагается, что поднимаемый столбик жидкости вертикален и имеет форму полого цилиндра с толщиной стенок, равной 2r. На самом деле поднимаемый столбик жидкости не имеет форму правильного полого цилиндра. В работах Гаркинса было показано, что в момент отрыва кольца
www.mitht.ru/e-library
