3. Примеси замещения с зарядом катионов меньшим, чем заряд катионов матрицы

Влияние на равновесие дефектов примеси замещения с зарядом катиона меньшим, чем заряд катиона матрицы, рассмотрим на примере замещения в матрице МеХ катионов Ме²⁺ катионами ’Ме⁺, происходящего при растворении ’Ме₂Х. В соответствии с формулой растворяющегося соединения, на каждый занятый при растворении анионный узел должно приходиться 2 узла, занятых катионами ’Ме⁺, в то время как в решетке матрицы соотношение катионных и анионных узлов 1:1. В результате при растворении неизбежно должны возникать точечные структурные дефекты. В данном случае вид дефектов различен для типов разупорядоченности «Френкель» и «Шоттки».

В кристаллах с типом разупорядоченности «Френкель» возможен переход катионов в междоузлия и невозможно образование вакансий аниона. Поэтому анион примеси занимает свободный анионный узел, один из катионов примеси также занимает свободный узел, а второй катион примеси вытесняет катион матрицы в междоузлие и занимает его место:

{2’Ме⁺_’Ме⁺·Х^2–_Х^2–}_прим + {□_Ме²⁺·□_Х^2– + Ме²⁺_Ме²⁺}_матр = 2++ + ,

или

0 = 2+; (76)

недостающие по отношению к нормальным зарядам двух катионов матрицы положительные заряды двух катионов примеси компенсируются зарядом межузельного катиона.

В кристаллах с типом разупорядоченности «Шоттки», напротив, возможно образование вакансий аниона и невозможен переход катионов в междоузлия. Поэтому оба катиона примеси занимают свободные узлы, анион примеси занимает свободный анионный узел, а второй анионный узел остается незанятым:

{2’Ме⁺_’Ме⁺·Х^2–_Х^2–}_прим + 2{□_Ме²⁺·□_Х^2–}_матр = 2++ ,

или

0 = 2+; (77)

недостающие по отношению к нормальным зарядам двух катионов матрицы положительные заряды двух катионов примеси компенсируются зарядом вакансии аниона.

Аналогичным способом для случая z_’Me < z_Me можно составить уравнения возникновения точечных структурных дефектов в кристаллах типов «Френкель» или «Шоттки» и при любом другом сочетании зарядов катионов примеси и матрицы.

Рассмотрим построение диаграммы, описывающей зависимость концентрации дефектов от давления металлоида, для кристалла с типом разупорядоченности «Френкель», содержащего катионную примесь замещения ‘Me⁺; диаграмма для типа «Шоттки» при том же составе матрицы, тех же значениях соответствующих констант равновесия, т. е. при K_Ш = K_Ф и K_Ш(Ме) = K_Ф(Ме), и той же концентрации ‘Me⁺, будет отличаться только тем, что будут заменены на .

Так же, как при построении диаграммы рис. 19, примем, что доля замещенных катионов составляет 0,004%, что соответствует концентрации примесных катионов (‘Me⁺) = 2·10^–5. В соответствии с уравнением (76), на каждые 2 катиона ‘Me⁺ приходится 1 катион в междоузлии, следовательно, концентрация «примесных» межузельных катионов ()_прим = 1·10^–5.

Равновесие дефектов при =

В отсутствие примеси _тепл = _тепл = = 1·10^-6; в присутствии примеси катиона ‘Me⁺ =_тепл + ()_прим, и поскольку ()_прим >> _тепл, принимаем ≈_прим = 1·10^–5; lg= -5.

Концентрацию вакансий катиона, отвечающую этой концентрации межузельных катионов, находим из условия =K_Ф: =K_Ф/=1·10^-12/1·10^–5=1·10^-7; lg= -7.

Концентрация электронов проводимости при в отсутствие примеси равна= 1·10^-12, а в кристалле с примесью ‘Me⁺ определяется равновесием процесса

0 D ↑ + 2e^– + , (78)

K_Ф(Ме) =(e^–)²(), (79)

откуда

(e^–) = ;

после подстановки K_Ф(Ме) = 1·10^–56, == 1·10^–52, =1·10^-5 получаем (e^–) = 3,16·10^-13, lg(e^–) = -12,5, в то время как в чистом кристалле при =(e^–) = 1·10^-12.

Таким образом, присутствие примеси катионов с зарядом меньшим, чем заряд катиона матрицы, вызывает уменьшение концентрации электронов проводимости по сравнению с чистым кристаллом, и поэтому такие примеси называют электроно-акцепторными (или просто акцепторными).

Концентрацию дырок определяем из соотношения (е⁺)=K_и/(е^-):

(е⁺) = 1·10^–24/3,16·10^-13 = 3,16·10^-12, lg(e⁺) = -11,5.

Наносим значения логарифмов концентраций дефектов на ось ординат, проведенную через точку оси абсцисс lg= -52.

Дальнейшие расчеты и построения выполнены точно так же, как в рассмотренном ранее случае z_’Me > z_Me; полученная диаграмма представлена на рис. 20.

Сравнение диаграмм, построенных для чистого кристалла (рис. 18) и кристаллов, содержащих примесь катиона, заряд которого выше (рис. 19) или ниже (рис. 20), чем заряд катиона матрицы, показывает, что акцепторная примесь, как и донорная, оказывает очень большое влияние на равновесие дефектов:

1. Даже при небольшом содержании примеси концентрация катионов в междоузлиях гораздо выше, а концентрация вакансий катионов гораздо ниже, чем в чистом кристалле.

2. Так же, как в случае донорной примеси, давление металлоида , при котором =и кристалл имеет стехиометрический состав, и давление металлоида , при котором (е^-) = (е⁺) и кристалл имеет минимальную (собственную) проводимость, не совпадают между собой и с давлением , при котором отсутствуют дефекты нестехиометрии. В присутствии примеси катиона, заряд которого ниже, чем заряд катиона матрицы, >>, а<.т. е. направления смещения и по отношению ку донорных и акцепторных примесей противоположны.

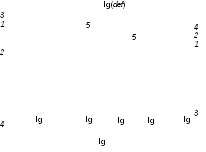
Рис. 20. Диаграмма зависимости равновесной концентрации дефектов от давления металлоида в кристалле МеХ, тип разупорядоченности «Френкель», содержащем акцепторную примесь ’Ме⁺

1 – катионы в междоузлиях; 2 – вакансии катионов; 3 – электроны проводимости; 4 – дырки; 5 – вспомогательные линии