Построение диаграммы

1. Выбираем интервал значений lgдля построения диаграммы. Ориентировочно можно принять, что ось абсцисс должна продолжаться в обе стороны отlgна Δlg= 30÷40; посколькуlg= -36,принимаем минимальное значение lg-70 и максимальное 0 (интервал значений -70≤lg≤ 0).

2. Проводим через точку на оси абсцисс lg=lg= -36 ось ординат; при выборе интервала значений ординат можно исходить из того, что точка (lg, lgK_и), отвечающая концентрации тепловых электронов проводимости и дырок, должна находиться посредине оси ординат, и от этой точки ось ординат должна продолжаться вверх и вниз примерно на 1,5 ÷ 2 разности логарифмов концентраций тепловых точечных структурных и электронных дефектов. В нашем случае lg(е^–)_т = = lg(е⁺)_т = -10, разность логарифмов концентраций тепловых точечных структурных и электронных дефектов равна 4; принимаем минимальное значение ординаты -18, максимальное -2.

3. Наносим на ось ординат (т. е. при lg=lg) точки, соответствующие концентрациям тепловых дефектов:

lg=lg= lgK_Ф = -6 и lg(e^–) = lg(е⁺) = lgK_и = -10.

Наносим также точку, соответствующую концентрациям электронов проводимости и дырок на границах между областями: ==-5,523.

4. Для того, чтобы найти положение границ между областями малых и больших отклонений давления от , нужноопределить, при каких значениях lglg(е^–) и lg(е⁺) достигнут значения ==-5,523.

Это легко сделать графически: lg и lg–абсциссы точек пересечения прямых lg(e^–) = f(lg) иlg(е⁺) = f(lg) с вспомогательной горизонтальной прямой, имеющей ординату-5,523. Для определения точек пересечения наносим на диаграмму вспомогательную линию и проводим через точку (lg, lgK_и) на оси ординат прямые lg(e^–) = f(lg) иlg(е⁺) = f(lg) с угловыми коэффициентами, равными соответственно -1/4 и +1/4. Через полученные точки пересечения прямых lg(e–) = f(lg) иlg(е⁺) = f(lg) с вспомогательной прямой проводим вертикальные линии – границы областей.

Более точный метод определения положения границ – аналитический. Расстояние от оси ординат до границы – это катет прямоугольного треугольника, вторым катетом которого является отрезок оси ординат между точками lgK_и и (lgK_Ф + lg3). Отношение катетов – это угловой коэффициент гипотенузы (т. е. прямых lg(e^–) = f(lg) иlg(е⁺) = f(lg) ∆y/∆x, следовательно, расстояние ∆x от оси ординат до границ можно найти, разделив отрезок оси ординат ∆y на угловой коэффициент соответствующей зависимости. В нашем случае

lg–lg= [-5,523 – (-10)]/(-1/4) = -17,91, lg= -53,91;

lg–lg= [-5,523 – (-10)]/(1/4) = 17,91, lg= -18,09.

Из точек на оси абсцисс с найденными значениями lgиlgпроводим вертикальные линии – границы между областями малых и больших отклонений.

Аналитический метод можно применять как единственный или использовать для контроля правильности графических построений.

5. Проводим через точку на оси ординат, соответствующую концентрации тепловых точечных структурных дефектов, горизонтальный отрезок в интервале lg≤lg≤ lg. Этот отрезок описывает зависимостиlg=f(lg) иlg= f(lg) в областях малых отклоненийот . Продлеваем прямыеlg(e^–) = = f(lg) иlg(е⁺) = f(lg) до границ областей соответственноlgиlg.

6. Из точек на границах областей проводим прямые, описывающие зависимости логарифмов концентраций дефектов от логарифма давления.

Полученная диаграмма показана на рис. 16.

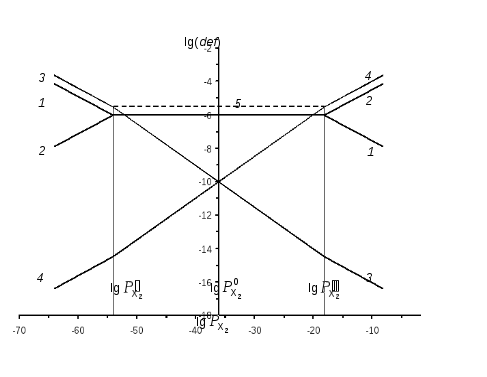
Рис. 16. Диаграмма зависимости равновесной концентрации дефектов от давления металлоида в кристалле Ме₂Х₃, тип разупорядоченности «Френкель»

1 – катионы в междоузлиях; 2 – вакансии катионов; 3 – электроны проводимости; 4 – дырки; 5 – вспомогательная линия