2. Соотношение между константами равновесия процессов возникновения недостатка и избытка металлоида

Константы равновесия процессов возникновения избытка металла (недостатка металлоида) K_Ф(Ме) и K_Ш(Ме) связывают с давлением металлоида равновесные концентрации электронов проводимости и межузельных катионов либо вакансий анионов, а константы равновесия процессов возникновения избытка металлоида (недостатка металла) K_Ф(Х) и K_Ш(Х) – концентрации дырок и вакансий катионов. Но концентрации электронов проводимости и дырок, межузельных катионов и вакансий катионов, вакансий анионов и вакансий катионов попарно связаны между собой константами равновесия тепловой разупорядоченности (константами равновесия типа произведений растворимости) – соответственно K_и, K_Ф и K_Ш. Следовательно, должны существовать выражения, связывающие между собой константы равновесия процессов возникновения избытка металла и процессов возникновения избытка металлоида и включающие константы равновесия тепловой разупорядоченности. То, что константы равновесия процессов образования дефектов нестехиометрии должны быть связаны между собой, подсказывает и простая логика: обе эти константы описывают один и тот же обратимый процесс обмена металлоидом между твердой и газовой фазами, и отличаются они только тем, какое направление перехода металлоида выбрано в качестве прямой реакции.

Найдем выражения, связывающие константы, для кристалла Ме₂Х₃ º 2Ме³⁺·3Х^2-.

Равновесия в кристалле с типом разупорядоченности «Френкель» описываются константами

K_Ф(Ме) = (e^–)³;

K_Ф(Х) = ;

K_Ф = ;

K_и = (e^–)(е⁺).

Выразим в первом уравнении концентрацию электронов проводимости через концентрацию дырок, а концентрацию межузельных катионов через концентрацию вакансий катионов:

K_Ф(Ме) = .

После преобразования полученного выражения получаем:

=.

Но выражение, стоящее в левой части равенства, – это не что иное, как K_Ф(Х), следовательно,

K_Ф(Х) =.

Теперь найдем соотношения между константами равновесия образования дефектов нестехиометрии в кристалле типа «Шоттки»:

K_Ш(Ме) = (e^–)²;

K_Ш(Х) = ;

K_Ш =;

K_и = (e^–)(е⁺).

Выразим в первом уравнении концентрацию электронов проводимости через концентрацию дырок, а концентрацию вакансий анионов через концентрацию вакансий катионов и затем преобразуем полученное выражение:

K_Ш(Ме) = ,

=.

Теперь возведем левую и правую части равенства в степень 3/2, чтобы получить концентрацию вакансий катиона в первой степени:

=.

Левая часть этого равенства - это выражение K_Ш(Ме), следовательно,

K_Ш(Ме) =.

3. Расчет равновесных концентраций дефектов при заданном давлении металлоида

   1. Составление и решение системы уравнений

Методику расчета равновесных концентраций дефектов при заданном давлении металлоида (подразумевается ≤≤) и известных значениях всех констант равновесия рассмотрим на примере кристалла Ме₂Х₃, тип разупорядоченности «Френкель». В таком кристалле присутствуют 4 вида дефектов: точечные структурные дефекты и и электронные дефекты e^– и e⁺. Для определения концентраций этих дефектов (т. е. расчета 4 неизвестных величин) необходимы 4 уравнения, связывающие равновесные концентрации дефектов между собой и с давлением металлоида.

Два из этих уравнений – это уравнения типа произведения растворимости, связывающие попарно равновесные концентрации дефектов между собой:

0 D + , = K_Ф, (I)

0 D e^– + e⁺, (e^–)(e⁺) = K_и. (II)

Третье уравнение – это уравнение, описывающее равновесие массообмена кристалла и газовой фазы (обратимого перехода металлоида из одной фазы в другую) и связывающее концентрации двух дефектов (одного точечного структурного и одного электронного) с давлением металлоида в газовой фазе. При этом можно использовать либо уравнение, описывающее уход металлоида из кристалла, либо уравнение, описывающее переход металлоида из газовой фазы в кристалл, но не оба вместе, так как на самом деле эти уравнения представляют собой два варианта записи одного и того же обратимого процесса. Соответственно обозначаем варианты третьего уравнения как IIIa и IIIб:

0 D ↑ + 3e^– + , (e^–)³=K_Ф(Ме), (IIIа)

↓ D 3e⁺ + ,(е⁺)³=K_Ф(Х). (IIIб)

Необходимо еще одно уравнение, связывающее между собой равновесные концентрации дефектов; этим уравнением будет математическое описание одного из обязательных условий равновесия – отсутствие в кристалле некомпенсированных электрических зарядов (условия электронейтральности кристалла). Поскольку в идеальном кристалле заряды катионов и анионов взаимно компенсируются, условие электронейтральности относится к зарядам дефектов и формулируется следующим образом: в равновесном кристалле сумма зарядов всех положительно заряженных дефектов равна сумме зарядов всех отрицательно заряженных дефектов.

Составим уравнение, описывающее условие электроней­тральности кристалла («уравнение электронейтральности») в самом общем виде, с учетом всех возможных дефектов, а не только характерных для какого-то одного типа разупорядоченности.

Пусть в единице объема кристалла содержится электронов проводимости,дырок,вакансий катиона,катионов в междоузлиях,вакансий аниона,анионов в междоузлиях. При этом положительный заряд всех дырок равен их числу(величина заряда дырки равна единице), положительный заряд всех катионов в междоузлиях равенz_Me(каждый межузельный катион несетz_Me положительных зарядов), а положительный заряд всех вакансий аниона равен z_Х(каждая вакансия аниона несетz_Х положительных зарядов). В результате суммарный положительный заряд всех положительно заряженных дефектов в единице объема равен

+ z_Me+ z_Х;

очевидно, суммарный отрицательный заряд в единице объема равен

+ z_Me+z_Х,

и в равновесном кристалле выполняется условие

+ z_Me+ z_Х=+z_Me+z_Х. (63)

Уравнение (63) связывает между собой числа дефектов в единице объема кристалла, а не их концентрации. Но поскольку концентрация дефекта – это отношение числа дефектов данного вида в единице объема кристалла к сумме чисел катионных и анионных узлов в единице объема (см. п. 2.4.1), для перехода к концентрациям достаточно почленно разделить левую и правую части равенства на =+:

+ z_Me+z_Х=+z_Me+z_Х,

откуда

(е⁺)+z_Me()+z_Х() = (e^–)+z_Me()+z_Х(). (64)

Применительно к кристаллу Ме₂Х₃ типа «Френкель», в котором , , e^– и e⁺ уравнение электронейтральности принимает вид

(е⁺)+3= (e^–)+3. (IV)

Теперь рассмотрим последовательность расчета равновесных концентраций дефектов при заданном давлении металлоида .

Поскольку при избытке металла целесообразно использовать уравнение (IIIа), а при избытке металлоида – уравнение (IIIб), а избыток металла или металлоида определяется тем, меньше или больше , чем , расчет необходимо начать с определения величины.

Расчет

При = дефекты только тепловые, и их концентрации определяются соотношениями, рассмотренными в п. 2.4.3:

_т = _т = ,

(e^–)_т = (е⁺)_т = .

Поэтому можно найти из уравнения(IIIа) или (IIIб) как давление металлоида , при котором концентрации дефектов имеют эти значения.

Воспользуемся уравнением (IIIа):

(e^–)³=K_Ф(Ме);

при =получаем:

()³=K_Ф(Ме) ()^–3/4;

()^3/4 = ;

= = .

С тем же успехом можно использовать уравнение (IIIб):

(е⁺)³=K_Ф(Х);

при =получаем:

()³=K_Ф(Х) ()^3/4;

()^3/4 = ;

= = .

Методика расчета для кристаллов с типом разупорядоченности «Шоттки» и различающимся числом катионов и анионов несколько отличается от описанной выше. Рассмотрим ее на примере кристалла того же состава.

Концентрации тепловых дефектов при = определя­ются соотношениями, также рассмотренными в п. 2.4.3:

= [(3/2)²K_Ш]^1/5,

= [(2/3)³K_Ш]^1/5,

(e^–) = (е⁺) = .

Подставим концентрации тепловых дефектов в уравнение, описывающее зависимость концентрации дефектов от давления металлоида при избытке металла:

(e^–)²=K_Ш(Ме),

K_и[(3/2)²K_Ш]^1/5 = K_Ш(Ме) ()^–1/2,

()^1/2 = ,

= .

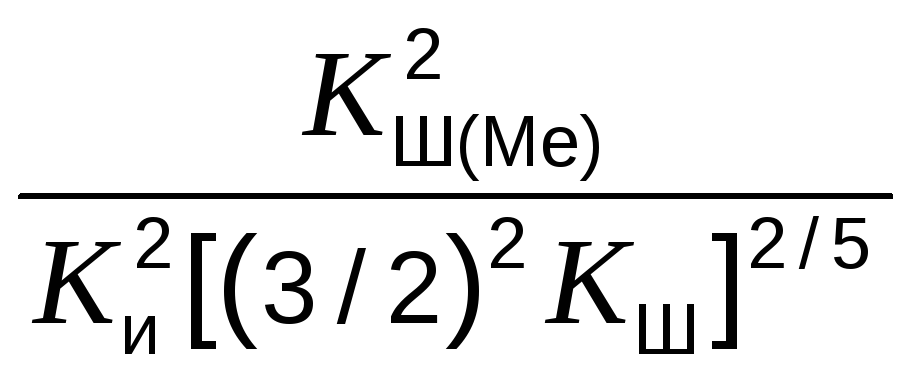При использовании уравнения для избытка металлоида:

(е⁺)³=K_Ш(Х),

= K_Ш(Х)()^3/4,

()^3/4 = ,

= .Расчет концентрации дефектов при ≠

Рассчитываем концентрацию дефектов в кристалле Ме₂Х₃ типа «Френкель» при < .

Система уравнений:

= K_Ф, (I)

(e^–)(e⁺) = K_и, (II)

(e^–)³=K_Ф(Ме), (IIIа)

(е⁺) + 3= (e^–) + 3. (IV)

Алгоритм решения: с помощью уравнений (I) – (IIIа) последовательно выражаем через концентрацию одного из дефектов концентрации всех остальных и подставляем в уравнение (IV); в результате получаем уравнение с одной неизвестной концентрацией и находим ее, а далее последовательно находим все другие концентрации. Целесообразно все концентрации выражать через концентрацию точечного структурного дефекта, входящую в уравнение (III) – независимо от формулы соединения и типа разупорядоченности, эта концентрация в уравнении (III) имеет степень, равную 1, что облегчает преобразования. В нашем случае это .

С помощью уравнения (I) выражаем концентрацию вакансий катиона:

= K_Ф.

С помощью уравнения (IIIа) выражаем концентрацию электронов проводимости:

(e^–) =

и с помощью уравнения (II) – концентрацию дырок:

(е⁺) = =.

Подставляем в уравнение (IV):

+ 3=+ 3K_Ф.

Перенесем все члены этого равенства в левую сторону и расположим в порядке убывания степени :

3+–– 3K_Ф= 0.

При известных значениях K_Ф, K_и, K_Ф(Ме) и заданном это уравнение имеет единственный действительный положительный корень, удовлетворяющий физическому смыслу. Как правило, для отыскания этого корня приходится использовать численные методы, хотя в некоторых случаях удается найти аналитическое решение. В частности, если все члены полученного уравнения умножить на, получим:

3+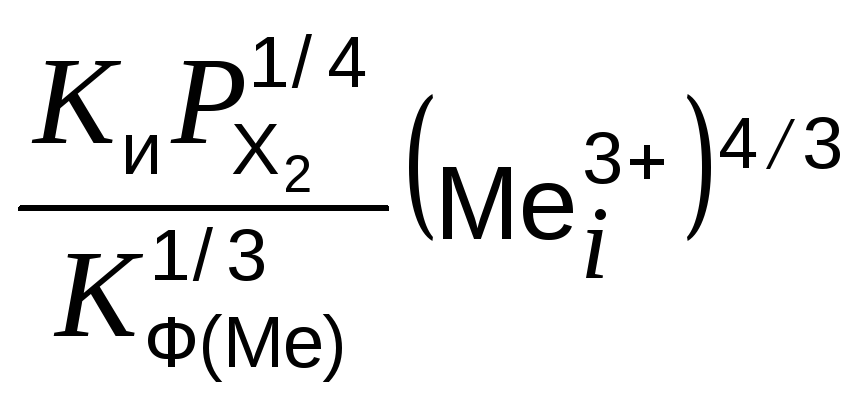–– 3K_Ф = 0,

и если обозначить =y, то уравнение превратится в кубическое типа

ay³ + by² + cy + q = 0,

корни которого находятся по известным формулам.

После определения расчет концентраций всех остальных дефектов не вызывает никаких сложностей.

Обычно представляет интерес не определение концентраций дефектов при одном заданном давлении металлоида, а построение зависимостей этих концентраций от в интервале от до . Для построения зависимостей необходимо достаточно большое число точек (иногда десятки, не менее 5 точек при < и столько же при > ), и даже при использовании компьютера расчеты требуют больших затрат времени и труда. Поэтому для построения зависимостей используют приближенный метод, не требующий никаких сложных вычислений.