
- •Раева в.М., Фролкова а.В. Основные законы равновесия жидкость – пар бинарных систем
- •Введение
- •1. Фазовые равновесия бинарных систем
- •1.1. Основные понятия
- •X' X''
- •1.2. Характеристики бинарных систем
- •2. Фазовое равновесие жидкость – пар бинарных систем
- •2.1. Основное уравнение фазового равновесия бинарных двухфазных систем
- •2.2. Законы Коновалова
- •Первый закон Коновалова
- •Второй закон Коновалова
- •Третий закон Коновалова
- •2.3. Законы Вревского
- •Первый закон Вревского
- •Второй закон Вревского
- •Второй закон Вревского
- •Третий закон Вревского
- •3. Эволюция бинарных азеотропов
- •Условные обозначения и сокращения
- •Литература
2.3. Законы Вревского
Законы Вревского описывают поведение систем при варьировании внешних параметров (температура, давление) при закрепленном составе жидкой фазы. Для их математической интерпретации получим раскрытую форму условия фазового равновесия в виде:
![]() (38а)
(38а)
![]() .
(38б)
.
(38б)
С учетом соотношений (20а), (21а) условие (38б) принимает вид:
![]() .
(39)
.
(39)
Раскроем полные дифференциалы разности химических потенциалов:
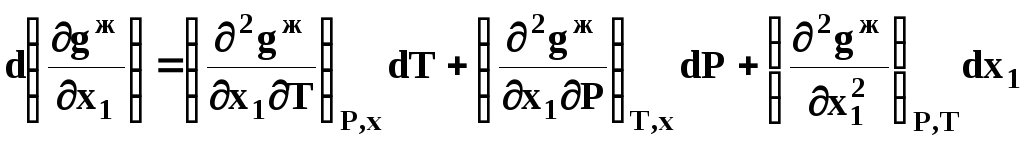 ,
(40а)
,
(40а)
 .
(40б)
.
(40б)
Величина
второй производной не зависит от порядка
дифференцирования (соотношения
Максвелла). Тогда, если представить
сомножители при переменных уравнений
(39) в виде частных производных
![]() потенциала:
потенциала:
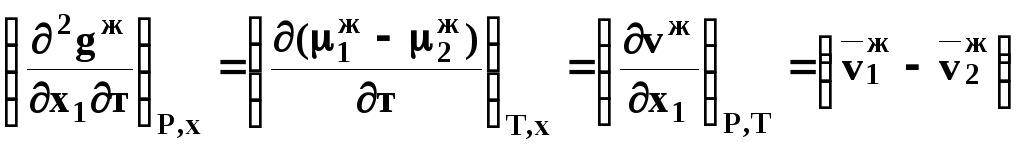 ,
(41)
,
(41)
получим:
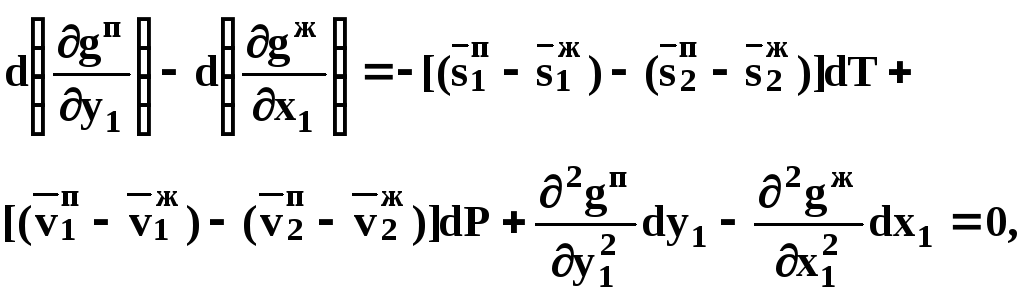 (42)
(42)
где верхней планкой обозначены парциальные величины. Последние были введены Льюисом для учета нелинейности зависимостей свойств бинарных смесей мы от состава.
В окончательном виде раскрытая форма условия фазового равновесия выражается следующим образом:
![]() .
(43)
.
(43)
Здесь
![]() .
.
При допущении об идеальном поведении паровой фазы и в условиях, удаленных от критических, объемная составляющая в уравнении (43) обращается в нуль.
Математический вывод законов Вревского базируется на анализе знаков всех величин, входящих в выражение (43). Их действие ограничено критическими точками фазового равновесия жидкость – пар.
Первый закон Вревского
Закон
определяет характер влияния внешних
параметров на содержание компонента в
паровой фазе при закрепленном составе
жидкой фазы. С учетом
![]() ,
выразим из (43) производную состава
паровой фазы по температуре:
,
выразим из (43) производную состава
паровой фазы по температуре:
![]() .
(44)
.
(44)
Для
идеального пара (![]() )
в условиях, когда объемом жидкой фазы
по сравнению с паровой можно пренебречь,
знак производной
)
в условиях, когда объемом жидкой фазы
по сравнению с паровой можно пренебречь,
знак производной![]() определяется знаком разности парциальных
молярных теплот испарения:
определяется знаком разности парциальных
молярных теплот испарения:![]() ,
если
,
если![]() .
.
При постоянном составе жидкой фазы и увеличении температуры пар всегда обогащается тем компонентом, парциальная молярная теплота парообразования которого больше.
Парциальные
молярные теплоты испарения определяются
через теплоты испарения чистых веществ
![]() и
парциальные избыточные энтальпии
компонентов
и
парциальные избыточные энтальпии
компонентов
![]() :
:
![]() .
(45)
.
(45)
При
отсутствии экспериментальных данных
о теплотах смешения (избыточных
энтальпиях) растворов парциальные
молярные теплоты испарения
![]() заменяют теплотами испарения чистых
веществ
заменяют теплотами испарения чистых
веществ
![]() .
Однако для зависимостей
.
Однако для зависимостей
![]() ,
имеющих экстремальные значения, замена
величин
,
имеющих экстремальные значения, замена
величин![]() теплотами испарения чистых компонентов
теплотами испарения чистых компонентов
![]() может быть
неправомерна. Например, для областей
составов (выделены отрезки на оси
абсцисс)
может быть
неправомерна. Например, для областей
составов (выделены отрезки на оси
абсцисс)
![]() (рис. 15а) и
(рис. 15а) и![]() (рис. 15б), знаки величин
(рис. 15б), знаки величин![]() и
и![]() противоположны.
противоположны.
Рисунок 15 иллюстрирует графическое определение парциальных величин. Значения интегральных теплот испарения
![]() (46)
(46)
совпадают
с аддитивными значениями
![]() только в случае атермических растворов,
где
только в случае атермических растворов,
где
![]() (рис. 15в).
(рис. 15в).
Второй закон Вревского
Закон
относится к изменению состава азеотропа
при варьировании температуры (давления).
Для азеотропа в уравнении (43)
![]() .
Раскрытая форма условия фазового
равновесия в этом случае имеет вид:
.
Раскрытая форма условия фазового
равновесия в этом случае имеет вид:
 .
(47)
.
(47)
Для идеального пара получаем уравнение Сторонкина-Морачевского, которое является математическим выражением второго закона Вревского:

