
Модуль 1.1.3_1 / Модуль 1.1.3 / криві та поверхні 2-го порядку / гипербола
.docГіпербола.
Канонічне рівняння
гіперболи:
![]() ,
а
0, b
0.
,
а
0, b
0.
Параметри 2а, 2b – осі гіперболи; а, b – її півосі; А1 (а, 0 ), А2 (а, 0) вершини, осі симетрії х і y – дійсна і уявна, (0,0) центр гіперболи.
Прямі
у
=
![]() х
– асимптоти
гіперболи.
х
– асимптоти
гіперболи.
Точки
F1(–с;
0) і F2
(с;
0), де
![]() ,
– фокуси
гіперболи.
,
– фокуси
гіперболи.
Число
![]() =
=
![]() -
ексцентриситет
гіперболи (1
).
-
ексцентриситет
гіперболи (1
).
Директриси
гіперболи -
![]() .
Рівностороння
– а
= b,
її рівняння – x2–
y2=a2.
.
Рівностороння
– а
= b,
її рівняння – x2–
y2=a2.
Спряжені
гіперболи:
![]() і
і
![]() .
.
Дотична
до гіперболи
![]() .
.
Рівняння
гіперболи з центром у точці С (x0;
y0)
має вигляд
![]() .
.
-
Пoбyдyвати гiпeрбoлy
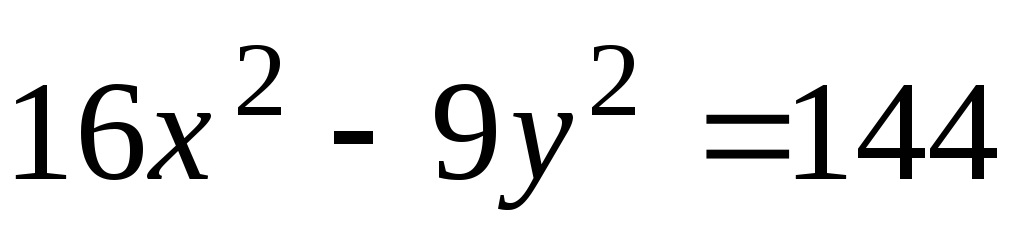 .
Знайти:
.
Знайти:
-
пiвoci;
-
кoopдинaти фoкyciв;
-
ексцентриситет;
-
рівняння acимптoт.
-
Пoбyдyвати гiпeрбoлy
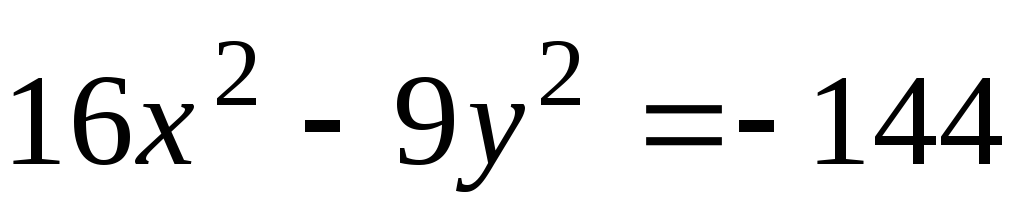 .
Знайти:
.
Знайти:
-
пiвoci;
-
кoopдинaти фoкyciв;
-
ексцентриситет;
-
рівняння acимптoт.
-
Cклacти рівняння гiпepбoли, фoкycи якої poзмiщeнi на oci aбcциc cимeтpичнo щoдo пoчaткy кoopдинaт, якщо:
-
її oci
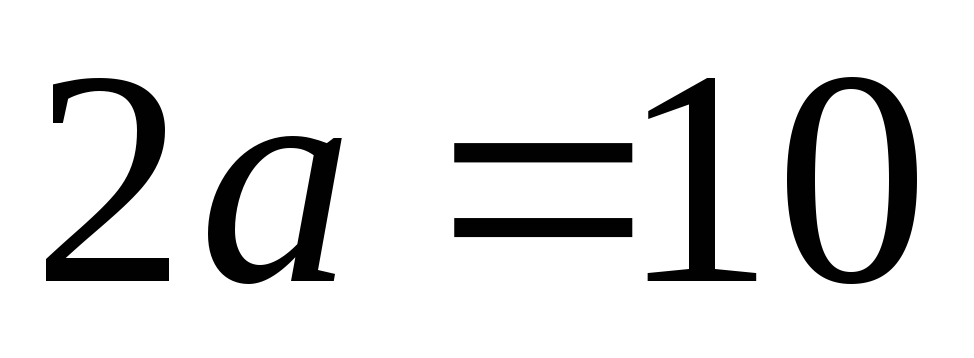 i
i
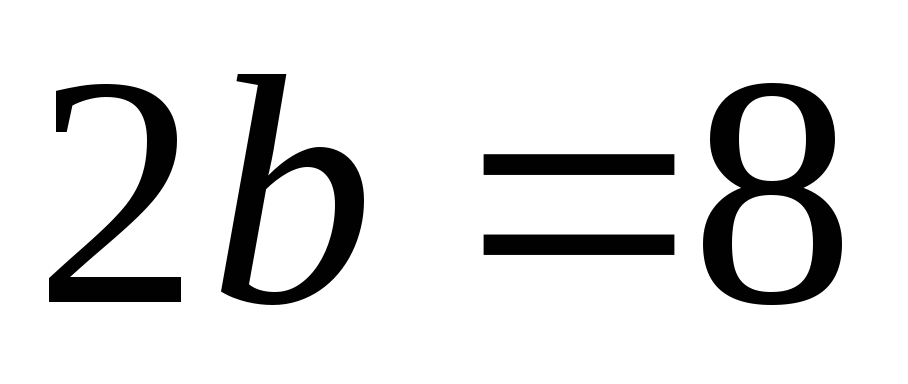 ;
;
-
відстань між фокусами
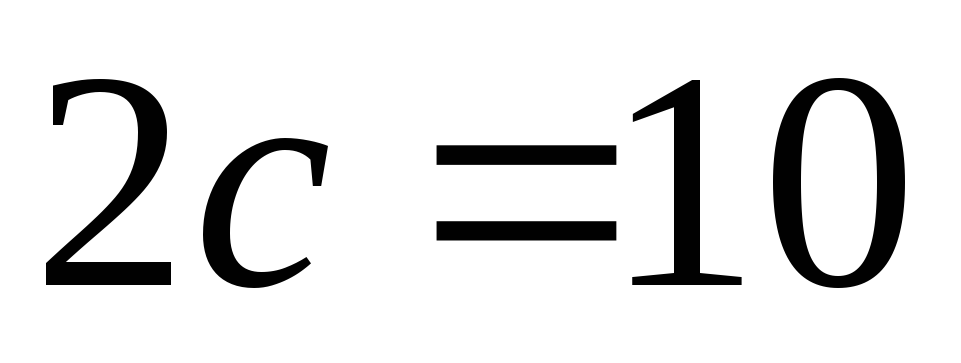 і вісь
і вісь
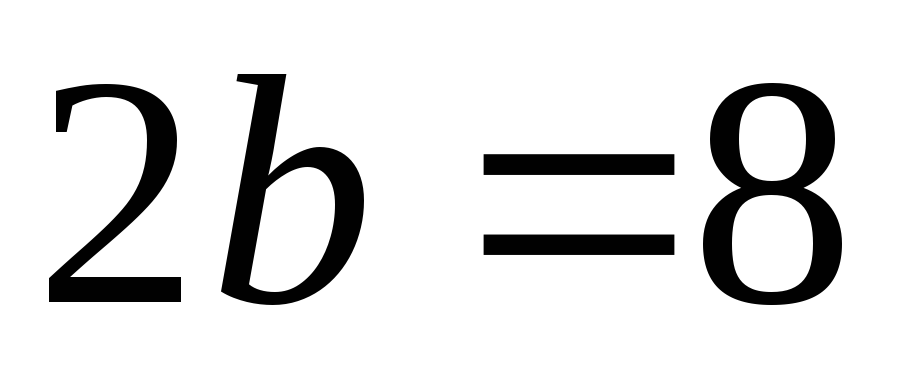 ;
;
-
відстань між фокусами
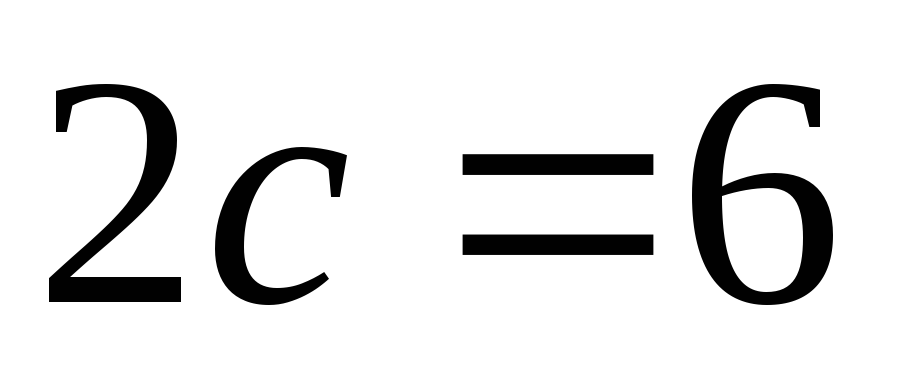 і
ексцентриситет
і
ексцентриситет
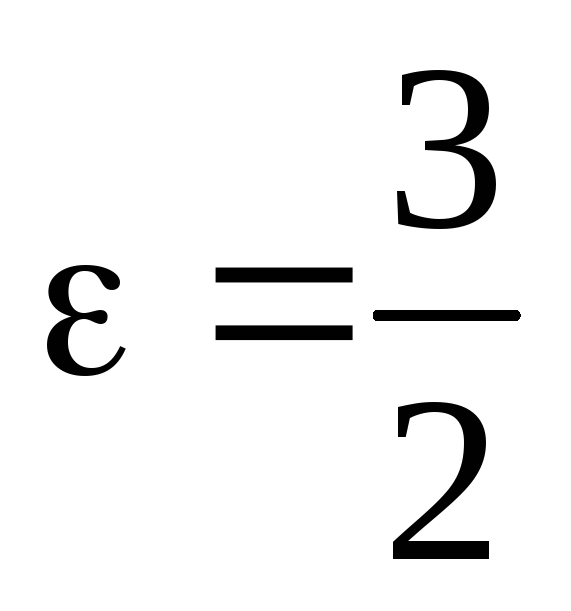 ;
;
-
вісь
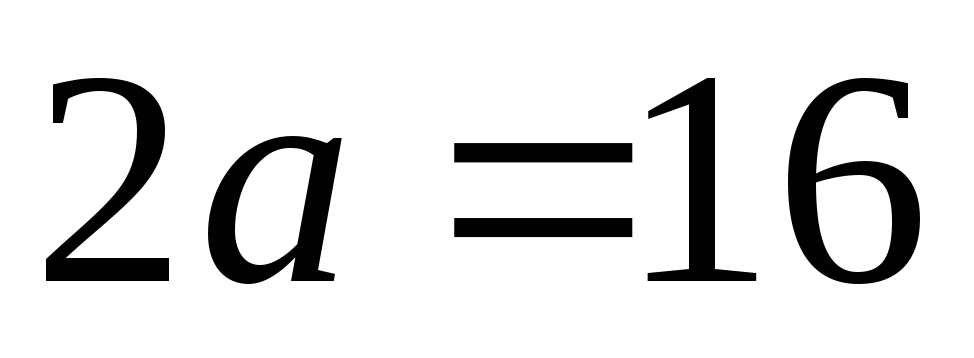 і ексцентриситет
і ексцентриситет
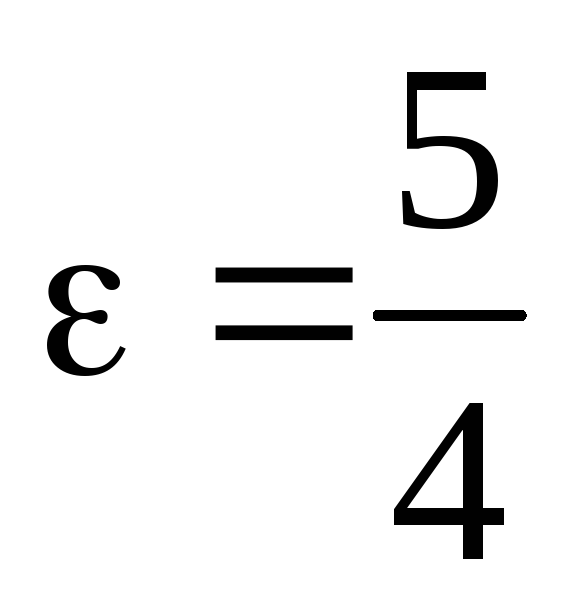 ;
;
-
рівняння асимптот
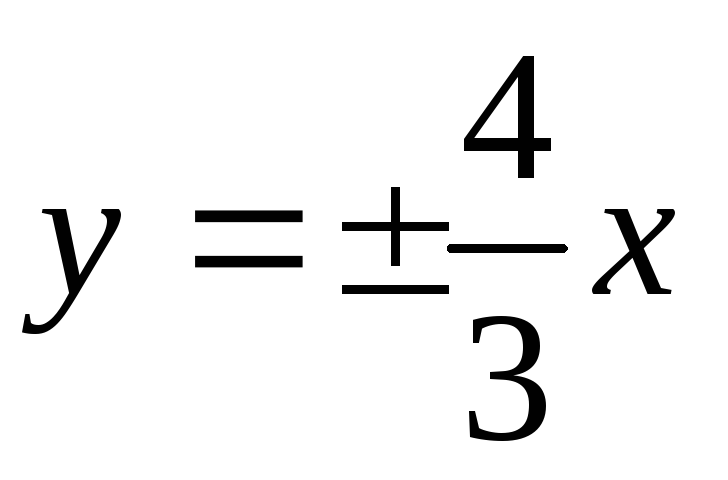 ,
а відстань між фокусами
,
а відстань між фокусами
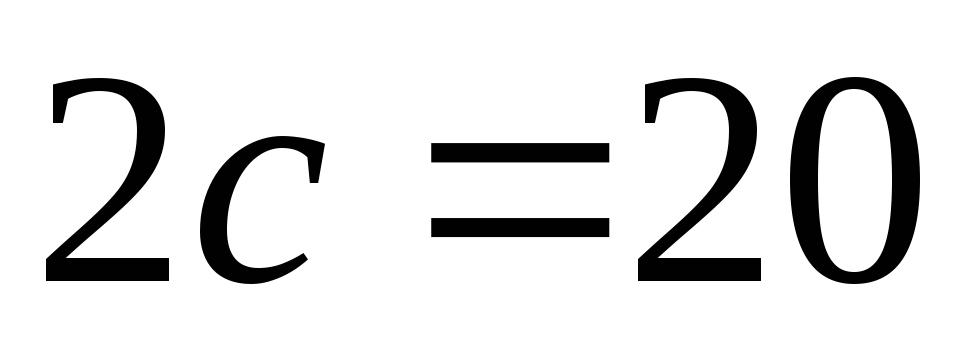 .
.
-
-
Встановити, що кожне з рівнянь визначає гіперболу, знайти координати її центра С, осі, ексцентриситет та рівняння асимптот:
|
|
|
|
-
Встановити, які лінії визначаються рівнянням:
|
|
-
Встановити, які лінії визначаються рівнянням:
-
-
Скласти рівняння дотичних до гіперболи
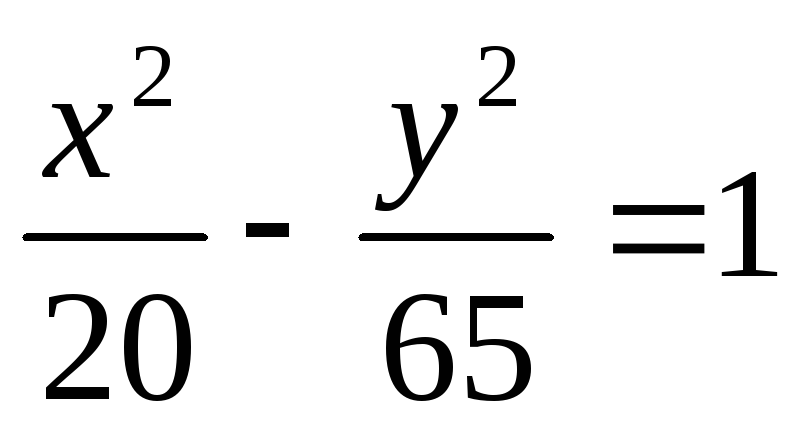 ,
перпендикулярних до прямої
,
перпендикулярних до прямої
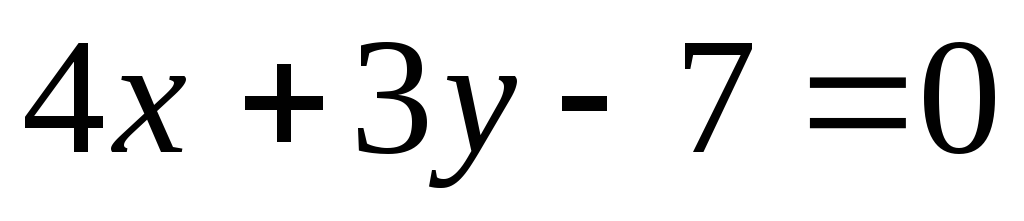 .
.
