
Модуль 1.1.3_1 / Модуль 1.1.3 / криві та поверхні 2-го порядку / парабола
.docПарабола.
Канонічне рівняння параболи:
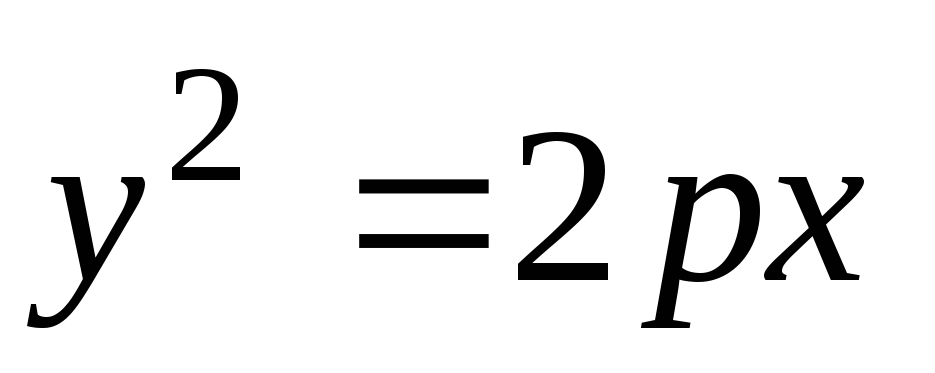 ,
,
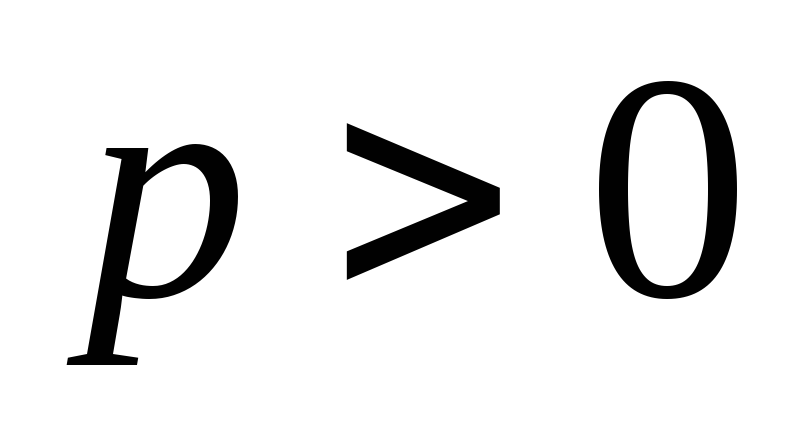 – параметр
параболи; точка
– параметр
параболи; точка
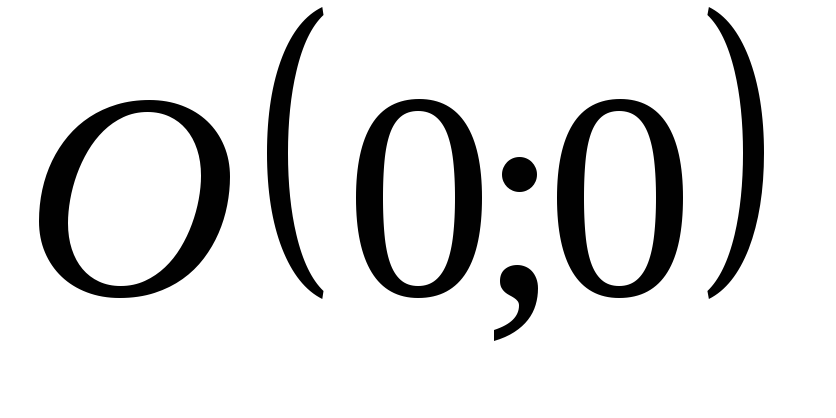 – вершина; вісь
– вершина; вісь
 – вісь параболи; точка
– вісь параболи; точка
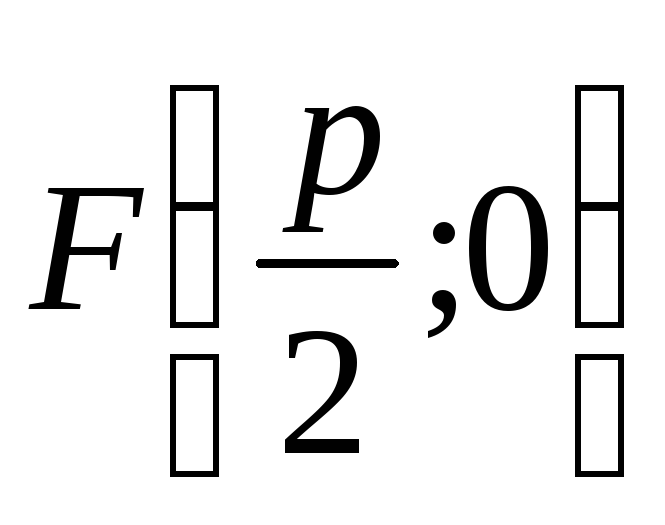 – фокус параболи.
– фокус параболи.
Пряма
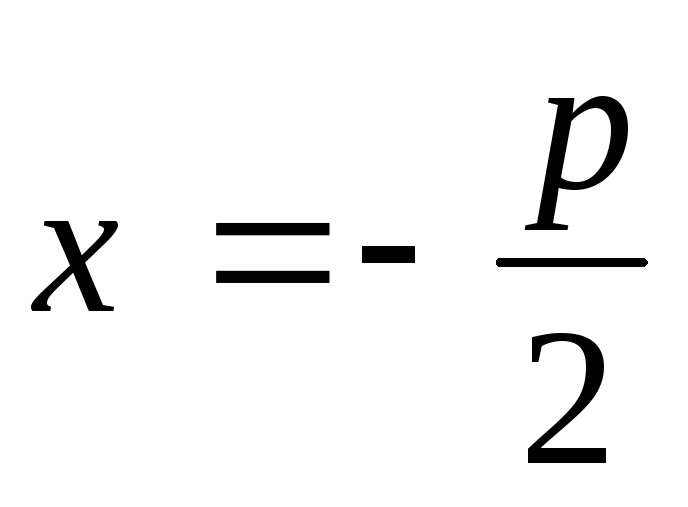 –
директриса параболи;
фокальний радіус точки
–
директриса параболи;
фокальний радіус точки
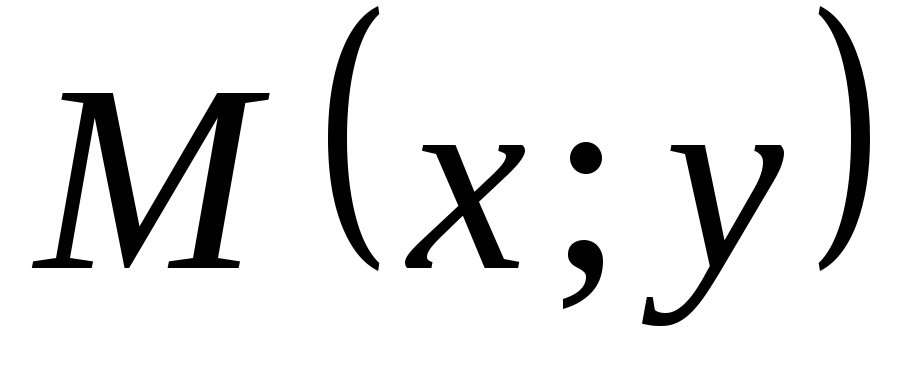 параболи визначається рівністю
параболи визначається рівністю
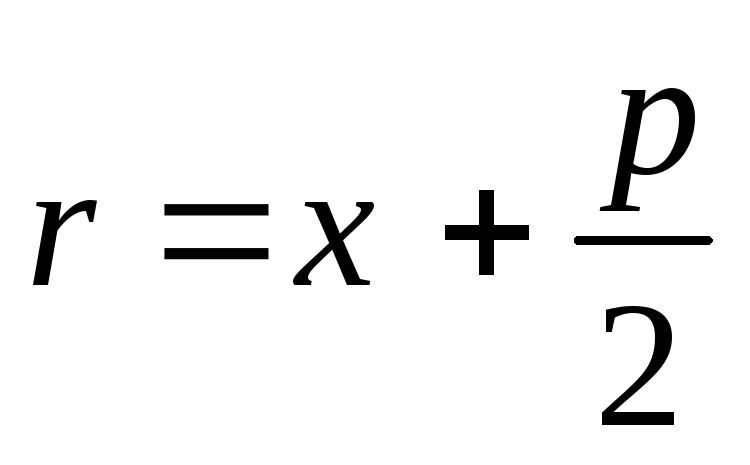 .
.
Рівняння параболи, симетричної
щодо осі
![]() з вершиною у початку
координат, має вигляд:
з вершиною у початку
координат, має вигляд:
![]() .
.
Фокус
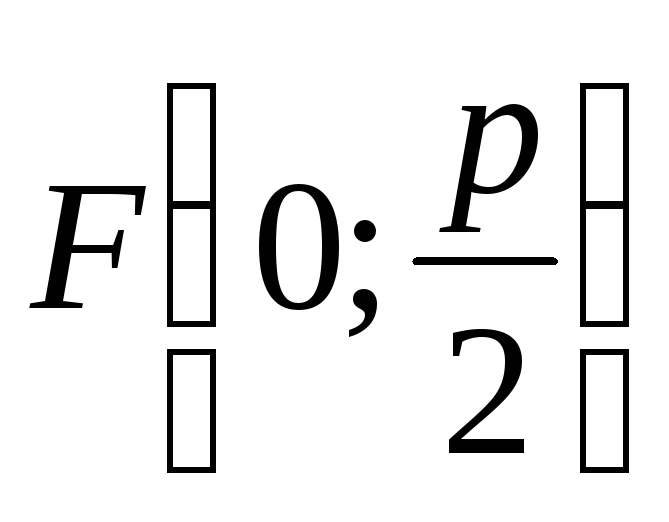 ;
;
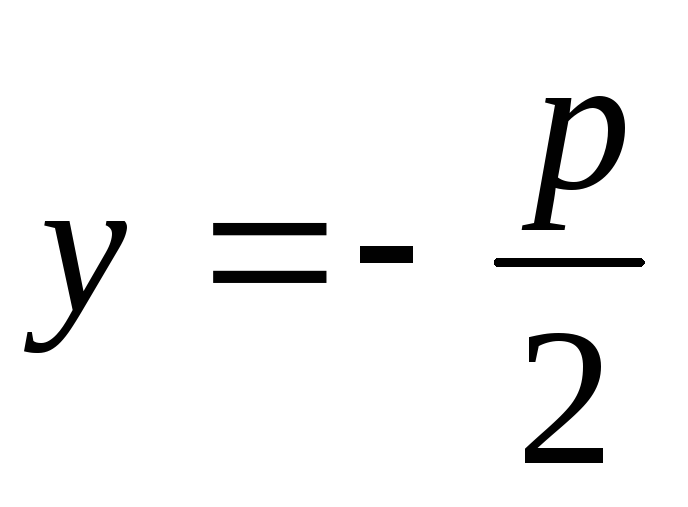 – директриса;
фокальний радіус точки M:
– директриса;
фокальний радіус точки M:
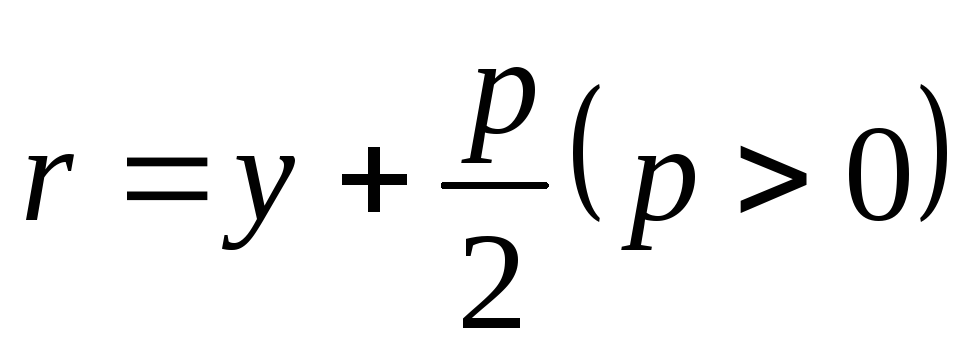 .
.
Ексцентриситет параболи
![]() .
.
Рівняння
![]() і
і
![]() .
.
Дотична до параболи
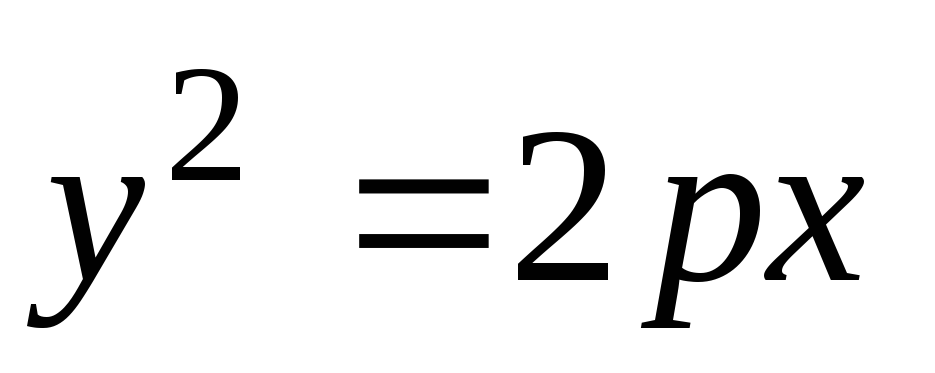 у точці
у точці
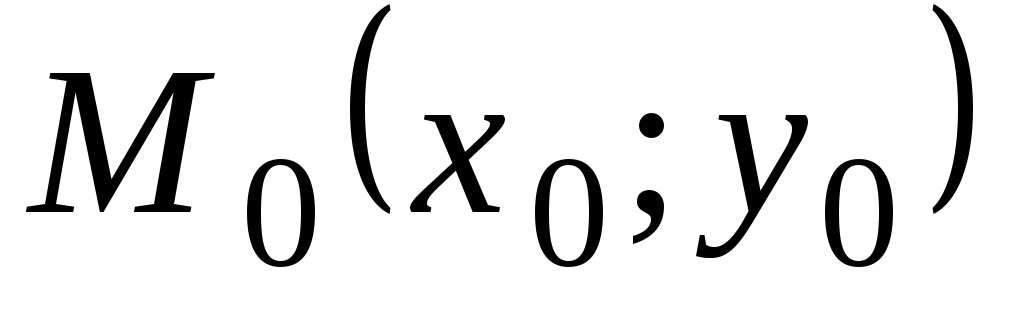 визначається рівністю:
визначається рівністю:
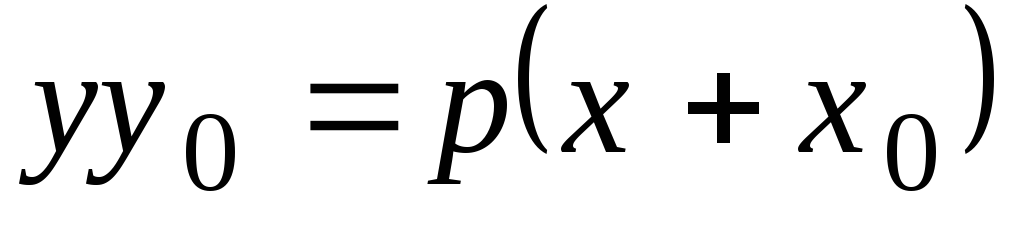 .
.
Рівняння параболи з вершиною
у точці
![]() має вигляд:
має вигляд:
![]() .
.
-
Знайти координати фокуса і рівняння директриси параболи
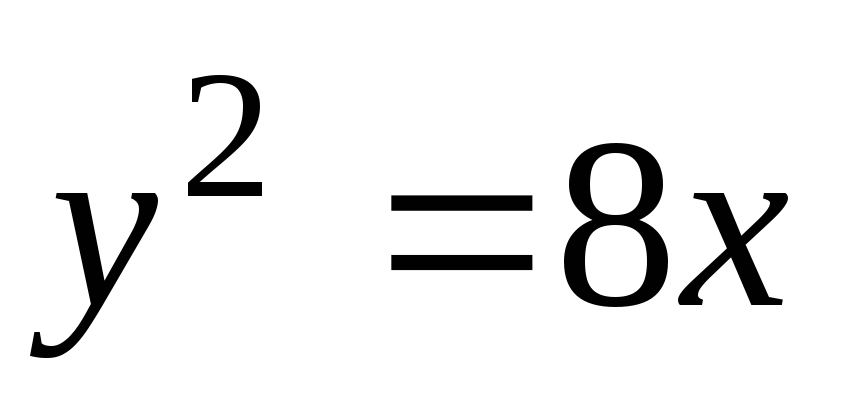 .
Обчислити довжину фокального радіуса
точки
.
Обчислити довжину фокального радіуса
точки
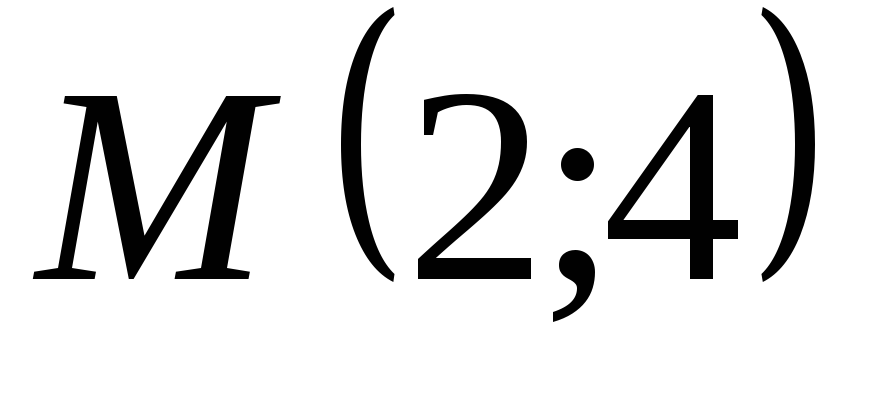 .
. -
Скласти канонічне рівняння параболи, якщо:
-
відстань фокуса, що лежить на осі
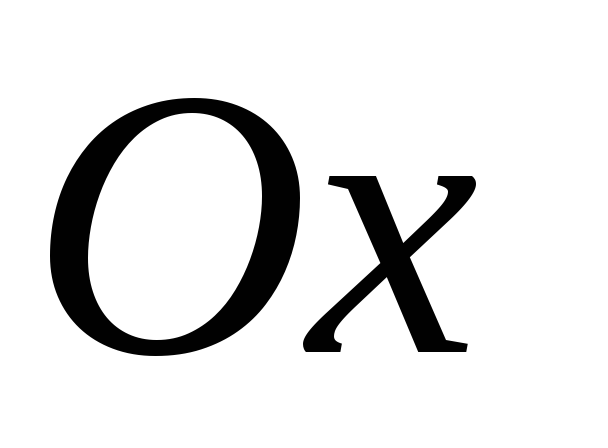 ,
до вершини дорівнює чотирьом;
,
до вершини дорівнює чотирьом; -
відстань фокуса, розміщеного на осі
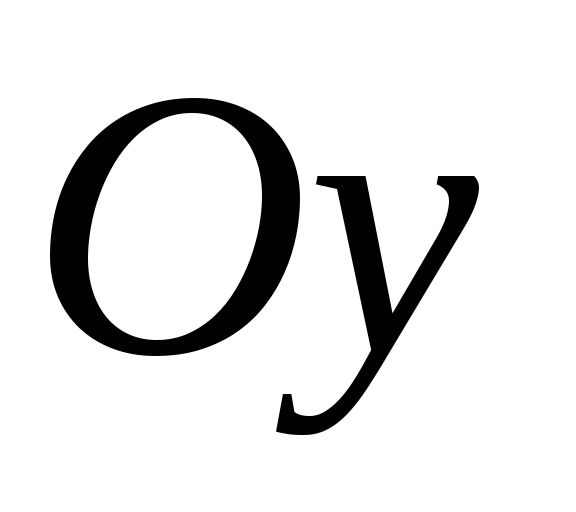 ,
до директриси дорівнює шести;
,
до директриси дорівнює шести; -
парабола симетрична щодо осі абсцис і проходить через точку
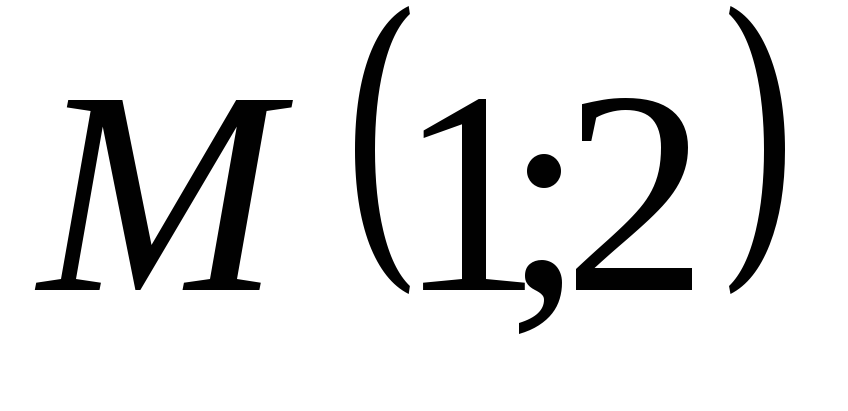 ;
; -
парабола симетрична щодо осі ординат і проходить через точку
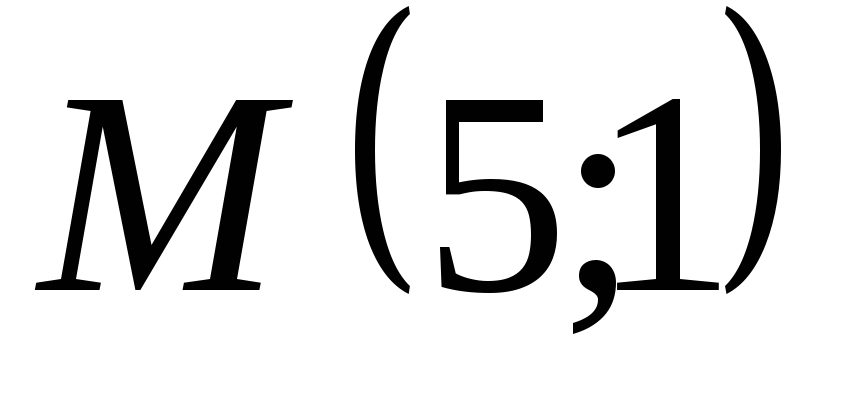 ;
;
-
-
Скласти рівняння параболи, якщо вершина її має координати
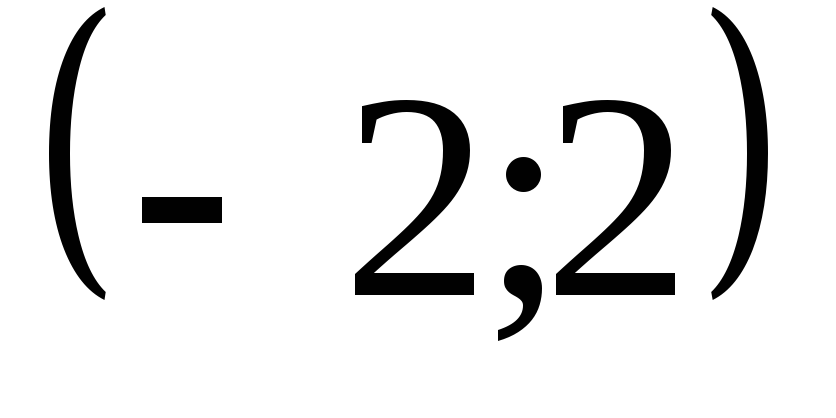 ,
параметр
,
параметр
 ,
а напрям її осі симетрії збігається:
,
а напрям її осі симетрії збігається:
|
|
|
|
Побудувати ці лінії.
-
Встановити, що кожне з рівнянь визначає параболу, знайти координати її вершини
 і величину параметра
і величину параметра
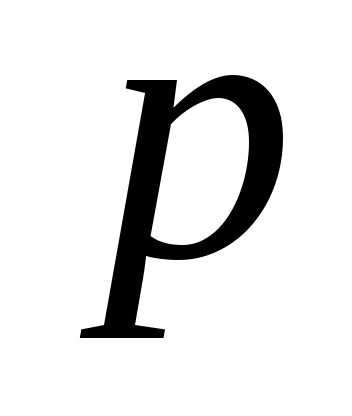 :
:-
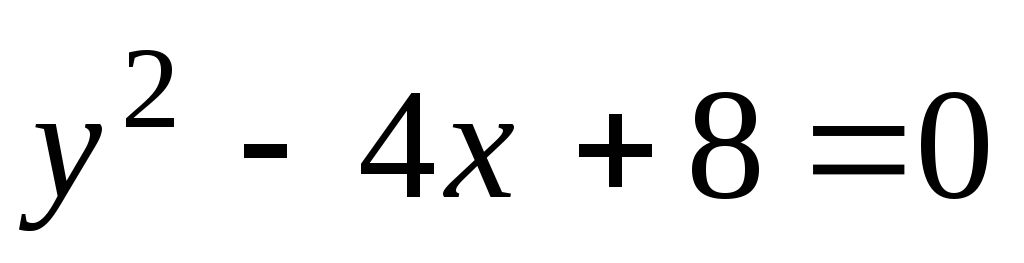 ;
;
-
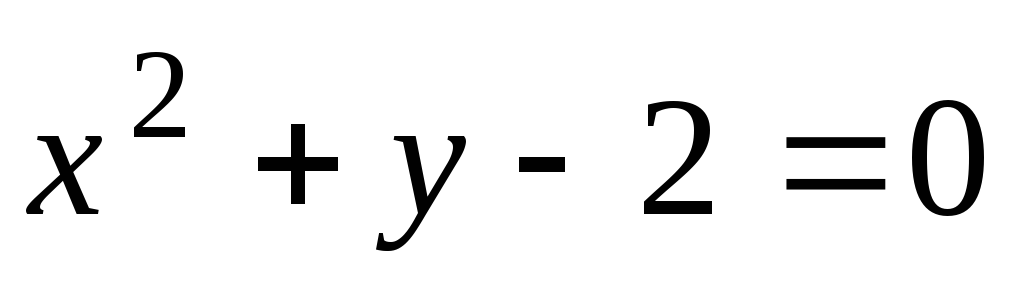 ;
;
-
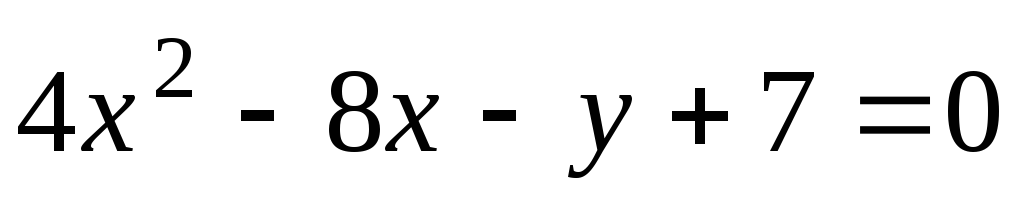 ;
;
-
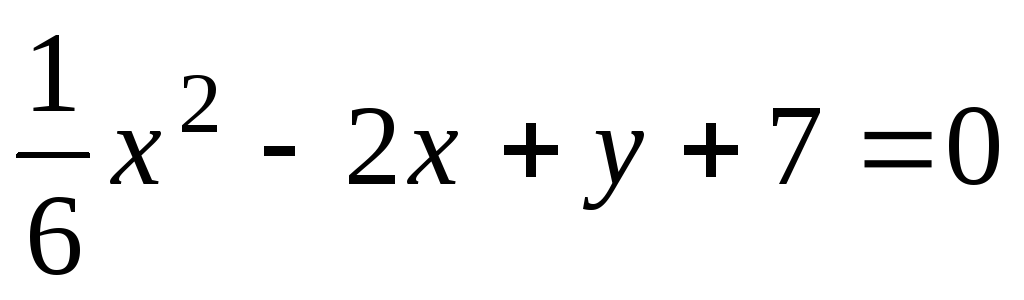 ;
;
-
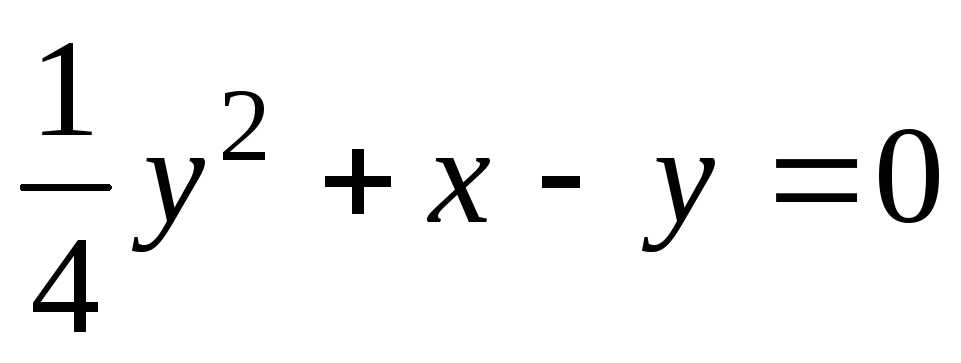 ;
;
-
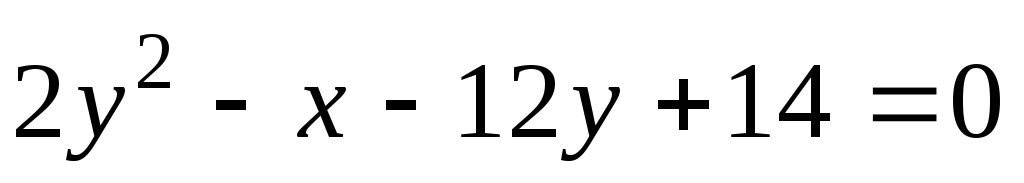 .
.
-
-
Встановити які лінії визначаються рівняннями:
-
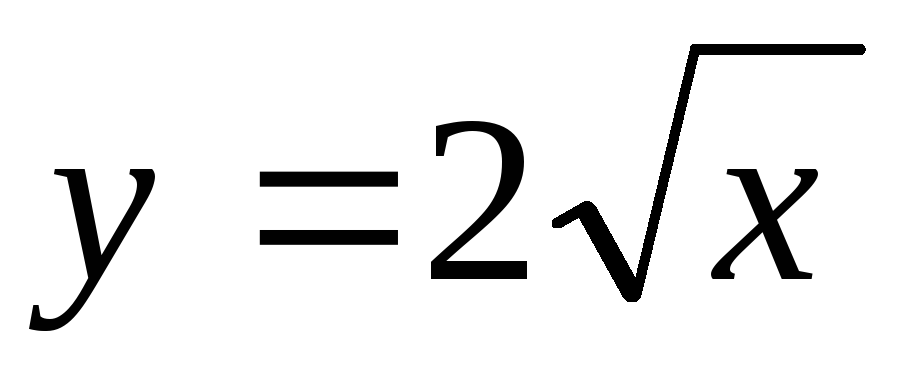 ;
;
-
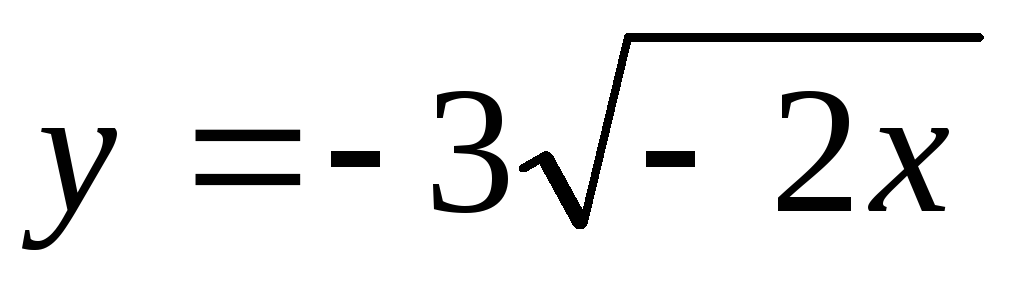 ;
;
-
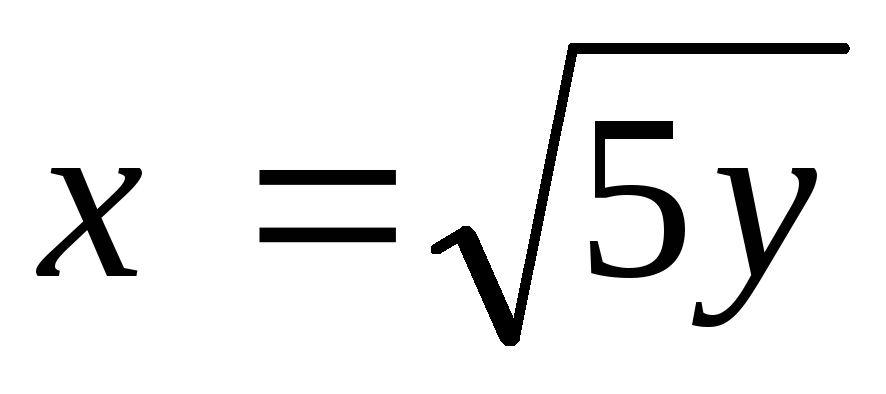 ;
;
-
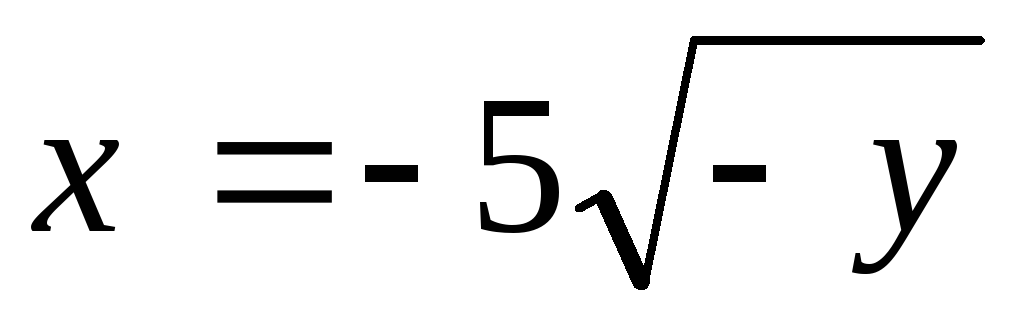 ;
;
-
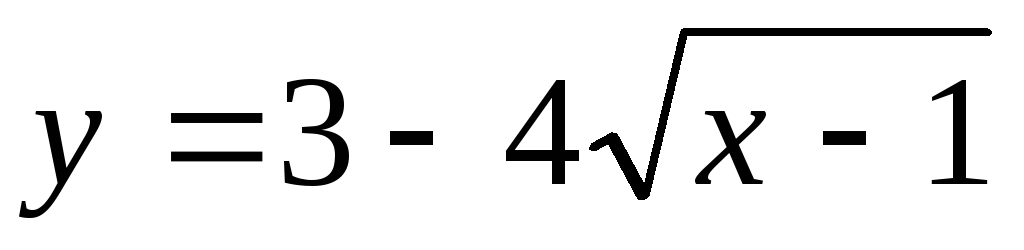 ;
;
-
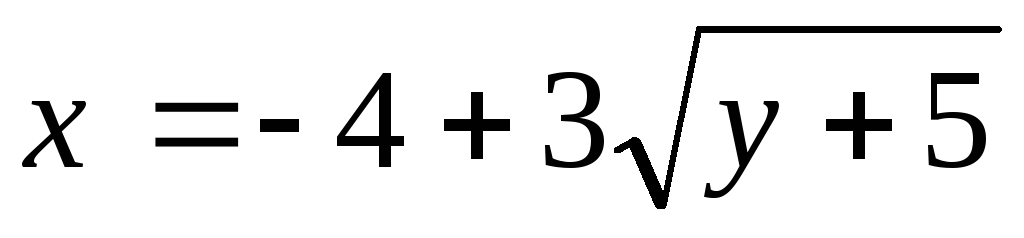 ;
;
-
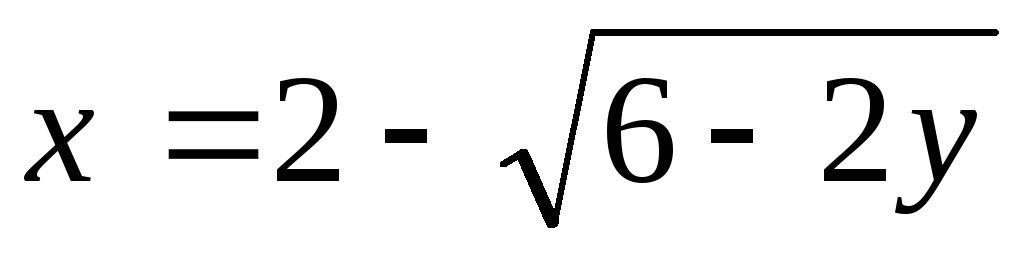 ;
;
-
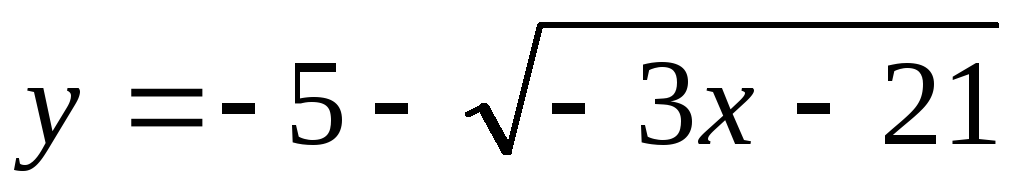 .
.
-
-
Пояснити геометричний зміст рівнянь:
|
|
|
|
|
|
|
|
|
|
