
Модуль 1.1.3 / Модуль 1.1.3 / Аналит. геометрія / криві 2-го порядку / кривые второго порядка
.PDF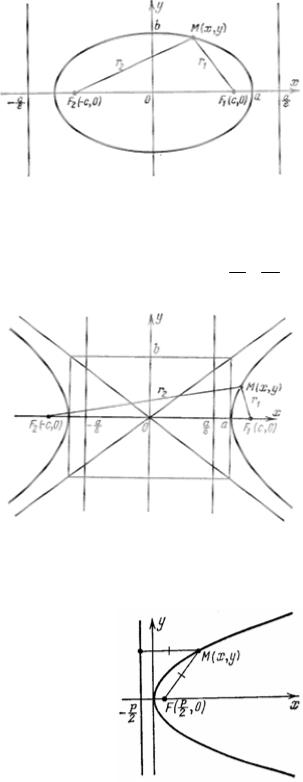
Кривые второго порядка
Определение 1. Эллипс – геометрическое место точек плоскости, сумма расстояний от которых до двух фиксированных точек F1 и F2 (фокусы эллипса) той же плоскости постоянна.
Теорема 1. Для любого эллипса найдется декартова система координат (фокусы лежат на оси абсцисс и
симметричны |
относительно |
начала координат), в которой уравнение этого эллипса имеет |
вид: |
x2 |
+ |
y2 |
=1 |
|
a2 |
b2 |
|||||||
|
|
Параметрическая форма: x = a cos t, y = bsin t, t [0, 2π] . |
|
|
|
|||
(каноническое |
уравнение). |
Величины |
a > b |
|||||
называются большой и малой полуосями эллипса.
Свойства эллипса:
•Эллипс имеет две взаимно перпендикулярные оси симметрии (главные оси эллипса).
•Эллипс имеет центр симметрии (центр эллипса).
•Эллипс можно получить из окружности
сжатием, т.е. преобразованием координат
y→ y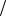 k .
k .
•Лучи света, исходящие из одного фокуса эллипса, после зеркального отражения от него, проходят через второй его фокус.
Определение 2. Гипербола – геометрическое место точек плоскости, модуль разности расстояний от которых до двух фиксированных точек F1 и F2 (фокусы гиперболы) той же плоскости постоянна.
Теорема 2. Для любой гиперболы найдется декартова система координат (фокусы лежат на оси абсцисс и
симметричны относительно начала координат), в которой уравнение этой гиперболы имеет вид:
(каноническое уравнение). Параметрическая |
форма: |
x = a ch t, y = bsh t, t (−∞, +∞) . Величины a |
и b |
называются действительной и мнимой полуосями
гиперболы.
Свойства гиперболы:
•Гипербола имеет две взаимно перпендикулярные оси симметрии (главные оси гиперболы).
•Гипербола имеет центр симметрии (центр гиперболы).
x2 − y2 =1 a2 b2
•Гипербола имеет асимптоты y = ± ab x
•Лучи света, исходящие из одного фокуса гиперболы, после зеркального отражения от нее, кажутся исходящими из второго ее фокуса.
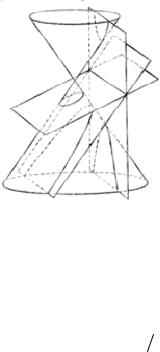
Определение 3. Парабола – геометрическое место точек плоскости, расстояния от которых до фиксированной точки F (фокусы параболы) и фиксированной прямой l (директриса параболы) той же плоскости равны между собой.
Теорема 3. Для любой параболы найдется декартова система координат (ось абсцисс перпендикулярна директрисе и проходит через фокус, ось ординат делит пополам расстояние между фокусом и директрисой), в которой уравнение
этой параболы имеет вид: y2 = 2 px (каноническое уравнение). Величина p
называется параметром параболы. Свойства параболы:
•парабола имеет ось симметрии (ось параболы).
•Гипербола имеет центр симметрии (центр гиперболы).
•Любые две параболы подобны друг другу.
•Лучи света, исходящие из фокуса параболы, после зеркального отражения от нее, образуют пучок параллельный оси параболы.
Теорема 4. Общее уравнение второго порядка в декартовых координатах на
плоскости a |
x2 +2a xy +a |
22 |
y2 |
+a x +a |
20 |
y +a |
00 |
= 0 описывает либо пустое |
11 |
12 |
|
10 |
|
|
множество, либо точку, либо прямую, либо пару прямых (параллельных или пересекающихся), либо эллипс, либо параболу, либо гиперболу. Все они объединяются названием кривые второго порядка (КВП).
Теорема 5. Произвольное сечение прямого кругового конуса плоскостью, не проходящей через его вершину, представляет собой либо эллипс, либо параболу, либо гиперболу. Любая из этих кривых может быть представлена как некоторое сечение прямого кругового конуса.
Теорема 6. Геометрическое место точек плоскости, отношение расстояний от которых до фиксированной точки F (фокус) к расстоянию до фиксированной прямой l (директриса) равно постоянной величине ε (эксцентриситет), является эллипсом (при ε <1 , в частности, окружностью при ε = 0 ), параболой (при ε =1) или
гиперболой (при ε >1 ). Для эллипса эксцентриситет равен отношению половины расстояния между фокусами к большой полуоси. Для гиперболы эксцентриситет равен отношению половины расстояния между фокусами к действительной полуоси.
Теорема 7. Пусть полюс полярной системы координат совпадает с одним из фокусов, а ось направлена вдоль оси симметрии эллипса, параболы или гиперболы в сторону противоположную ближайшей вершине. В такой
системе координат уравнение этой кривой имеет вид ρ = |
p |
. Здесь ε |
– эксцентриситет, а p – параметр |
1 −ε cosϕ |
|||
для параболы или p = b2 a для эллипса или гиперболы. |
|
|
|
