ЛАБОРАТОРНАЯ РАБОТА №4

ОПРЕДЕЛЕНИЕ УСКОРЕНИЯ СИЛЫ ТЯЖЕСТИ

ЦЕЛЬ РАБОТЫ: ознакомиться с характеристиками колебательного движения физического маятника; определить ускорение силы тяжести различными способами.

ОБОРУДОВАНИЕ: математический и физический маятники, масштабная линейка, осветитель с фотодиодом, электронный частотомер-хронометр или специальная установка.

Краткая теория

Частным случаем физических маятников является так называемый оборотный маятник. Оборотные маятники, в зависимости от предъявляемых к ним требований, имеют самую различную форму. В настоящей работе применяется оборотный маятник, изображенный на рис. 1.

Н

Рис. 1. Оборотный

маятник

а металлическом стержнеА опорные призмы В жестко закреплены и не передвигаются. Жестко закреплена и чечевица С, находящаяся между ними. Вторая чечевица Д находится на конце стержня (за призмами) и может перемещаться. Ее положение фиксируется при помощи линейки, неподвижно закрепленной на стержне. Маятник ставится одной из опорных призм на неподвижно укрепленный кронштейн. При отклонении от положения равновесия маятник совершает колебательные движения. На кронштейне имеется отверстие малого диаметра, которое играет роль точки подвеса математического маятника (шарика на двойной нити (рис.2)). Нить закреплена на барабане, вращением которого можно изменять длину нити маятника, а следовательно, и его период колебаний. Двойная нить (бифилярный подвес) берется для того, чтобы колебания шарика происходили строго в одной плоскости. По периоду колебаний математического маятника Т определяется ускорение силы тяжести g в данной точке земной поверхности. При этом используется известное соотношение

, (1)

где L — длина математического маятника.

Приведенной длиной маятника следует считать расстояние от точки подвеса до центра качания шарика. Центр качания можно определить как математическую точку, в которой нужно сосредоточить всю массу маятника, чтобы период его колебаний остался без изменений. Однако, непосредственное определение приведенной длины маятника может быть произведено недостаточно точно, поэтому поступают следующим образом. Измеряют длинуL = L₁ + r, где r — радиус шарика, и его длину L = L₂ + r. Затем измеряют периоды свободных колебаний Т₁ и Т₂ маятников двух различных длин

L и L. Из формулы (1) имеем:

.

В

Рис.2. Математический

маятник

ычитая из первого выражения второе, получите формулу (2) для определения ускорения силы тяжести с помощью математического маятника. При таком способе измерения исключается необходимость измерения положения центра качания шарика.

Для определения периода колебаний используется установка, схема которой изображена на рис. 3.

Рис. 3. Блок-схема установки.

1. частотомер;

2. источник питания;

3. фотодиод;

4. флажок на маятнике;

5. источник света.

Если фотодиод закрыт флажком и не освещен, то ток в цепи слабый, т.к. темновое сопротивление фотодиода велико. При отклонении флажка фотодиод освещается, его сопротивление уменьшается и величина тока в цепи возрастает. Таким образом, во время колебаний маятника фотодиод периодически то закрывается, то освещается, соответственно, изменяется и величина электрического тока в цепи. Включенный последовательно (или параллельно) в цепь частотомер-хронометр фиксирует периодичность возникающих в цепи электрических сигналов.

УПРАЖНЕНИЕ 1

Измерения

Удостоверившись в работоспособности установки, включите приборы в сеть. Поставьте все переключатели, тумблеры и регуляторы электронного частотомер-хронометра в рабочий режим для измерения периода колебаний (необходимые данные получите у лаборанта). Установите длину маятника L и измерьте ее. Расположите осветитель и фотодиод так, чтобы в положении равновесия маятника свет на фотодиод не попадал. Отведите математический маятник на небольшой угол, отпустите шарик, предоставив ему возможность свободно колебаться.

Измерьте период колебания маятника несколько раз и запишите данные в таблицу. Форму таблицы разработайте самостоятельно.

Установите новую длину маятника L, опустив шарик как можно ниже, и измерьтеL.Затем несколько раз измерьте период колебания маятника при этой длине и данные занесите в таблицу.

Рассчитайте ускорение свободного падения gпо вашей формуле (2). Определите погрешностьgкак для косвенного измерения.

Более точное определение ускорения свободного падения можно произвести с помощью оборотного маятника.

УПРАЖНЕНИЕ 2

Применение оборотного маятника основано на свойстве сопряженности центра качания и точки подвеса. Это свойство заключается в том, что на всяком физическом маятнике можно найти такие две точки, что при последовательном подвешивании маятника за ту или другую из них, период колебания маятника останется одним и тем же. Расстояние между этими точками равно приведенной длине данного маятника.

Если амплитуда колебаний маятника мала, то период колебания определяется формулой

, (3)

где I— момент инерции физического маятника относительно оси подвеса;

m— масса маятника;

L— расстояние между осью качания и центром тяжести маятника.

По теореме Гюйгенса-Штейнера

, (4)

где I₀— момент инерции маятника относительно оси, проходящей через центр тяжести и параллельной оси качаний.

Из уравнений

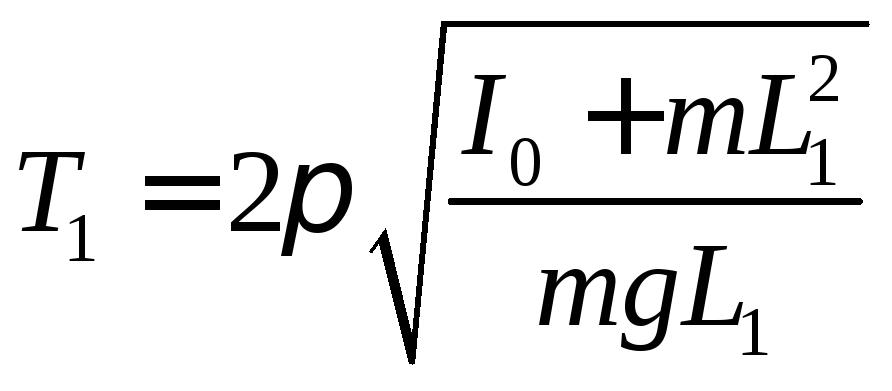,имеем

.

Для величины ускорения из последней формулы после преобразований получаем формулу Бесселя

. (5)

Если периоды колебаний равны между собой, тоТ₁=Т₂=Ти уравнение (5) примет вид

. (6)

Но добиться полного равенства периодов нелегко. Однако формула (5) Бесселя позволяет достаточно просто и с хорошей точностью определить величину ускорения при приближенном равенстве периодов колебаний.

Перед тем, как начинать систематические измерения, необходимо подумать о том, какие следует выбрать условия опыта, чтобы точность измерений оказалась наибольшей. Чтобы ответить на этот вопрос, изучим прежде всего зависимость периода колебаний Тот расстоянияLдо оси качания. Рассмотрим формулу. Эта зависимость имеет вид кривой, изображенной на рис. 4.

Рис. 4. График зависимости Т = f(L)

При L 0 периодТ∞, как. ПриL∞, сноваТ∞, на этот раз как. ПриТ>Т_minодно и то же значениеТдостигается при двух разных значенияхL. Эти разные значения должны быть найдены на опыте и использованы для вычисленияg.Как ясно из приведенного графика, при измененииТвеличиныL_1, L₂сближаются или удаляются друг от друга.

Разберем вопрос о том, как точность определения gзависит от разностиL₁ - L_2. Пусть значенияТ₁ иТ₂ , которые нам кажутся равными, на самом деле отличаются на малую величину 2Т, так что

_.(7)

Величина 2Топределяет, таким образом, точность совпадения периодов.

С помощью формул (7) вместо формулы (5) найдем (пренебрегая выражением Т²)

.

Введем обозначение

.

Так как при достаточно малых значениях величинахбудет мала, то можно воспользоваться разложением в ряд (пренебрегая членами второго и выше порядков)

,

что приводит к формуле

. (9)

В этой формуле выражение, стоящее перед скобкой, совпадает с (6), а член, вычитающийся из единицы, определяет относительную расчета g:

. (10)

Формула (10) определяет ошибку вычисления g, связанную с ошибкой измерения времени и длин. Из этого выражения видно, что относительная ошибкаg/gнеограниченно возрастает, если разность (L₁–L₂ ) стремится к нулю, т.е. еслиТ Т_min(см. рис.4). Условия опыта, таким образом, должны выбираться так, чтобыL₁иL₂ отличались друг от друга достаточно сильно. Измерения обычно обеспечивают хорошую точность в определенииg, если.