6. Парам ур плоскости. Ур пл, проход через 3 зад тчк. Ур пл в отрезках.

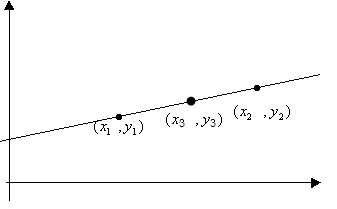
Дано: т М0(z0,y0,z0) лежащ на плоск, a, b – не компл векторы на плоск. т М – тчк на плоск, 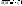плоск. Вектa и b образ базис множ-ва всех векторов пл-сти, следовательно вектор может быть разложен по базису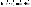, гдеu,v – параметры. (u,v) – координаты вект в базисе {a,b}, - парам ур пл-сти. В координатах:

Ур пл через 3 зад тчки: 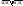,- компл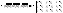

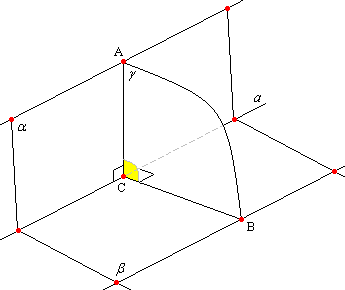
Ур пл на осях: Рассмотрим плоскость не проход через нач координат и пусть плоск отсекает от оси Ох – отрезок а, Оу – b, Oz – c.

7. Расст от тчк до пл. Норм ур плоскости.

Ax+By+Cz+D=0; умножим на нормирующий множитель

- единичный вектор нормали, если отложить данный вектор от начала координат, то он будет направлен в сторону пл-сти. 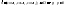, р – расст от нач корд до пл-сти Дакажем что р – расст от нач корд до пл:

т.к. Р принадл плоскости;

Расст тот точки до пл: расстояние со знаком плюс если точка и начало координат лежат по одну сторону. Теорема: расст от до пл с заданным норм ур-ем равноД-во:

; Замечание: расст можно нах по формуле:

8. Взаимн расп двух пл-ей в простр. Угол между пл.

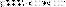; 1) Пересекаются

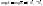
2) Прараллельны: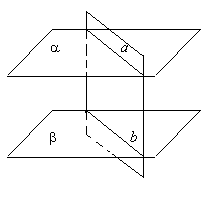

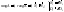
3) Совпадают;

Угол межд пл: При пересеч двух пл-стей получаются две пары вертикальных углов, наименьший назовем углом межд пл-ми. Вычисляется как угол между норм вект-ми.

9. Прямая в простр. Общ ур пр. Ур пр, проход через 2 заде тчки.Параметрич., конанич. уравнения прямой.

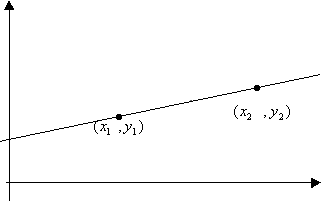
1) Общ ур-я:

2) парам ур прям: иa=(l,m,n) – направ вект (не равен 0); - парам ур прям в вект виде;

3) Конан ур: 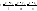- конан ур-ие

Ур прямой проход через 2 зад тчки: В качестве 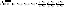или

10. Взаимн располож двух пр, пр и пл в простр.

1) параль 2 пр:

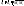
2) совп 2 пр

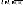
3) пересек 2 пр

3) скрещ 2 пр

прям и пл: прямая - 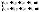, плоскость –Ax+By+Cz+D=0; если система ур имеет одно решение – прям пересек пл, если бесконечное кол-во решение – лежит в ней, если не имеет решения – параллельна

11.Расстояние от точки до прямой, двумя прямыми в пространстве

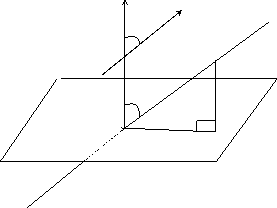
Строим пар-мы на векторах Расстояние между скрещивающимися прямыми. Угол между прямой и плоскостью ; ;;;

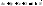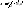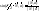4.Линии и поверхности второго порядка

1. Эллипс. Вывод канонического уравнения. Свойства.

Опр: Эллипсом наз сножесто точек плоскости, сумма расстояний от которых до 2 заданных точек есть величина постоянная.Заданые точки – наз фокусами эллипса.(F1,F2)

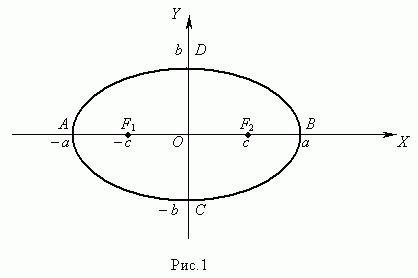
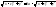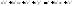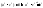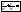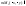; , т.е. а и с- параметры, а>c ;;;;;т.к.a>c , то ;;- канонич ур-ние эллипса в канонич системе координат.a и b- параметры, а- большая полуось b- малая полуось. Свойства: 1) пересечение с осями координат: с Ох: с Оу;вершины эллипса. 2) Симметричность:эллипсу => эллипс симметричен относительно Оу.эллипсу => симметричен относит Охэллипсу => О-ценр симметрии эллипса. 3) Эллипс расположен в ограниченной части плоскости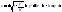;4) Эллипс можно получить из окружности с помощью сжатия или растяжения;;;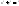

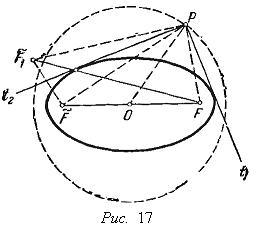
5) Параметрические ур-ния эллипса: ;

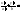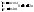
6) Эксцентриситет 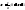;отрезок;окружность(с=0).