AlgStr / Практические занятия / Матрица / Практическая работа №1_2

Практична робота № 2

Схеми зберігання розріджених матриць.

Спосіб 1: Упакований спосіб зберігання розріджених матриць. Зберігаються всі ненульові елементи

рядок стовбець

Якщо  ненульові символів, то необхідно 3 комірок. При збереженні в упакованому вигляді розрідженої матриці необхідно передбачити можливість додавання нових ненульових елементів.

а) Використання зв'язаних списків.

Кожному елементу a_ij0 відповідає у пам’яті запис, який зберігається по стовбцям, тобто елементу a_ij буде відповідати деякий запис j- стовбця матриці. Кожен запис уявляє собою впорядковану трійку

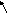
Номер рядку Значення Покажчик на наступний

елемент

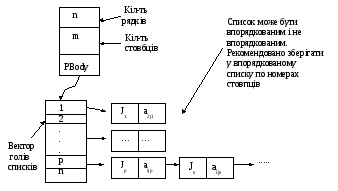
Представлення такої матриці складатиметься з масиву голів списків ненульових елементів по стовпцях і списку трійок <i, а, p> для кожного ненульового елементу стовпця.

Цю схему можна використовувати в перевернутому вигляді, тобто по рядках. Тоді масив голів списків зберігатиме покажчики на списки ненульових елементів рядків.

На мові Turbo Pascal реалізація має наступний вигляд:

type

PNode = ^Node; (покажчик на вузол)

Node = record

j: word ; (використовується для індексу стовпця)

Vol: real; (значення матриці a_ij)

Next: Pnode;

end;

PtrArray = array [1...65520 div SizeOf(PNode) of PNode];

Matr = record

n,m: word;

PBody: PtrArray;

end;

PMatr = ^Matr;

Іноді корисні упаковки, що не використовують зв'язаних списків. Для них потрібна менша пам'ять, але додавання і видалення ненульових елементів вимагає зрушення елементів масиву. Нижче описуються чотири такі схеми.

б) Використання одновимірних масивів (векторів)

Схема І (nxm) (по стовпцях)

Кожному елементу матриці відповідає запис, який має наступний вигляд:

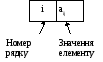
Нуль в першому осередку означає кінець даного стовпця. Другий осередок в цьому випадку містить номер наступного стовпця. Нулі в обох осередках указують на кінець масиву, що зберігає матрицю. Число осередків, необхідних для зберігання матриці, розраховується по формулі

2 (n + τ +1)

Розглянемо застосування Схеми І на прикладі:

Ця матриця для якої τ = 7, n = 5 зберігатиметься у вигляді масиву:

(0, 1; 2, a₂₁; 4, a₄₁; 0, 2; 5, a₅₂; 0, 3; 1, a₁₃; 3, a₃₃; 0, 4; 2, a₂₄; 0, 5; 4, a₄₅; 0, 0)

0

1

2

а21

4

а41

0

2

5

а52

0

0

0

Номер

стовпця, де є ненульові

елементи

Нумеруємо пари для обчислення розміру вектора:

ℓ = (n+1+ τ)- максимальний розмір числа пар

τ - повинно зберігатися в образі матриці або обчислюватися, але може зберігатися

і в дескрипторі.

При описі типу за даною схемою виникає проблема, яка складається у наступному: j_i-ціле, a_ij1- може бути будь-яким, тому використання значень цих пар різне. При цьому використовується тип запис з варіантами.

type

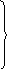Para=record

case K: word of тип i-ї пари , яка дорівнює 0 j_i

0: (j:word); i a_iji

else (val: real);

end;

Схема II

Інформація про дану матрицю зберігається в трьох масивах: VE - значення ненульових елементів, RI - індексів рядків і CIP - покажчиків індексів стовпців. Елемент RI(α) містить індекс рядка α-ого елементу VE - VE(α). Якщо перший ненульовий елемент β-ого стовбця даної матриці розміщується в VE(t_β), тоді t_β зберігається в β-ому елементі CIP, т.ч. CIP(β) = t_β. Очевидно, VE та RI складаються з τ елементів, а CIP з n елементів. Отже ця схема вимагає загальне число в 2τ + n комірок.

Матриця A₅ зберігатиметься таким чином:

VE = (a₂₁, a₄₁, a₅₂, a₁₃, a₃₃, a₂₄, a₄₅)

RI = (2, 4, 5, 1, 3, 2, 4)

CIP = (1, 3, 4, 6, 7)

Вищевикладеною схемою легко користуватися. Наприклад, a₃₃ може бути знайдене таким чином. Оскільки CIP(3) = 4, тоді RI(4) дасть індекс рядка першого ненульового елементу третього стовпця. Якщо a₃₃ ≠ 0, тоді RI(4) або один з наступних за ним елементів RI передуючих першому ненульовому елементу четвертого стовпця, повинен бути рівний 3. У нашому випадку RI(5) = 3, т.я. VE(5) містить a₃₃.

Схема III

Кожному ненульовому елементу даної матриці однозначно ставиться у відповідність ціле число λ(i, j) вигляду:

λ(i, j) = i + (j – 1)n, a_ij ≠ 0

Зберігання ненульових елементів забезпечується двома масивами: VE - значень ненульових елементів і LD, в кожному з яких міститься τ елементів. В LD(α) знаходиться λ(i, j), відповідне a_ij з VE(α), де α = 1,2, …, τ.

Матриця A₅ зберігається у вигляді:

VE = (a₂₁, a₄₁, a₅₂, a₁₃, a₃₃, a₂₄, a₄₅)

LD = (2, 4, 10, 11, 13, 17, 24)

Елементи зберігаються по стовпцях.

PVE - елементи;

PLD - приведений індекс елементу в суцільному уявленні по стовпцях.

Початкова матриця може бути відновлена по цій схемі зберігання таким чином. Відповідно до даним вище визначенням для λ(i, j) є очевидним, що j є найменше ціле, більше або рівніше λ(i, j)/n та i = λ(i, j) – (j -1)n.

Наприклад, якщо λ(i, j) = LD(5) = 13, тоді λ(i, j)/n =13/5 і найменше ціле число більше або рівніше λ(i, j)/n буде 3 та i = λ(i, j) – (j -1)n = 13 – 10 = 3.

Схема IV

Якщо A - симетрична матриця, в якій для всіх i ≥ j a_ij = 0, i – j > θ_i, де θ_i набагато менше n і в загальному випадку може мати різні значення для кожного i, то така матриця називається симетричною стрічковою матрицею з шириною стрічки, що локально змінюється.

У такій матриці можна запам'ятовувати тільки елементи на головній діагоналі і нижче. Зберігається матриця у вигляді двох масивів:

VE - значення ненульових елементів і ;

PD - положення діагональних елементів в масиві VE.

Для кожного рядка в VE зберігаються крайній лівий ненульовий елемент і всі наступні елементи, розташовані праворуч від нього аж до діагонального включно. Тому i-й рядок матриці A вимагає θ_i + 1 комірок для зберігання і VE складатиметься з n

∑ θ_i + 2n комірок для зберігання матриці A.

i=1

Наприклад, хай у нас є матриця

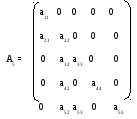
Тоді її можна представити у вигляді:

1 2 3 4 5 6 7 8 9 10 11 12

VE = (a₁₁, a₂₁, a₂₂, a₃₂, a₃₃, a₄₂, 0, a₄₄, a₅₂, a₅₃, 0, a₅₅)

PD = (1, 3, 5, 8, 12)

Елемент a_ij початкової матриці може бути відновлений таким чином. Положення a_ij у VE визначається значенням PD(i) – (i – j), якщо тільки PD(i) – (i – j) > PD(i – 1). Остання умова означає, що a_ij не лежатиме ліворуч від першого ненульового елементу i-ого рядка, інакше a_ij = 0 і не зберігається в VE.

Наприклад, щоб знайти елемент a₅₃ у масиві VE, обчислюємо PD(5) – (5 – 3) = 12 – 2 = 10 > 8 = PD(4) і, отже, a₅₃ зберігається в VE(10).

Головна перевага цієї схеми упаковки полягає в наступній. Якщо в процесі обчислень, наприклад, при виключеннях по методу Гауса, створюються додаткові ненульові елементи тільки вправо від крайнього лівого елементу кожного рядка, то вони можуть запам'ятовуватися в VE без переміщень всіх наступний за ними елементів.

Діагональна блочна форма (BDF)

Матриця A визначена формулою:

Має форму BDF, якщо для всіх i ≠ j підматриці A_ij = 0 и всі діагональні підматриці A_ij є квадратними матрицями.

Трикутна блочна форма (BTF)

Матриця A задана у вигляді:

причому підматриці A_ij = 0 для i ≠ p та підматриці A_ii, i = 1, 2, …, p є квадратними матрицями, то говорять, що матриця A має трикутну блокову форму BTF.

Трикутна стрічкова форма (BNTF)

Говорять, що матриця B має трикутну стрічкову форму, якщо існує таке β 0 ≤ β ≤ n, де b_ij = 0 для всіх i – j > β, та значення β не може бути зменшено перестановками рядків і стовпців матриці B.

Хай перший ненульовий елемент i-ой рядка матриці B знаходиться в q_i-ому стовбці. Тоді визначаємо:

β _i = i- q_i, q_i ≤ i

β _i = 0, q_i > i

Очевидно, що якщо матриця B має форму BNTF, то max β _i = β .

Відмітимо, що трикутна блочна форма (BTF), описана в попередньому розділі, є спеціальним випадком BNTF (β + 1 є в цьому випадку розміром найбільшого діагонального блоку матриці B).

Стрічкова форма (BF)

Визначення. Матриця A, у якої a_ij = 0 при |i – j| > β, називається стрічковою матрицею. Якщо до того ж a_ij ≠ 0 для всіх |i – j| ≤ β, то вона називається повною стрічковою матрицею. Величина 2β + 1 називається шириною стрічки.