AlgStr / Машина Тьюринга

Машина Тьюринга

Одним из первых формальных определений алгоритма было определение английского математика А.М.Тьюринга. В 1936 году он описал схему некоторой абстрактной машины, состоящей из бесконечной ленты и автомата, и предложил называть алгоритмом то, что умеет делать эта машина. При таком определении то, что не может быть сделано машиной Тьюринга не является алгоритмом. Компьютеры также предназначены для выполнения алгоритмов, но это реальные устройства, тогда как машина Тьюринга является абстракцией. Абстрагируемся мы от конечности памяти.

Машина Тьюринга состоит из бесконечной в обе стороны ленты, разделенной на ячейки и автомата. В каждой ячейке может находиться один из символов алфавита, в котором представляются данные. Если ячейка пустая, то говорим, что в ней находится пустой символ. Алфавиты могут быть разные, но для каждой конкретной машины Тьюринга выбирается какой-либо один алфавит. Автомат может двигаться вдоль ленты и по очереди "обозревать" содержимое ячеек. Входное слово размещается на ленте по одной букве в расположенных подряд ячейках и занимает конечное число ячеек. Слева и справа от входного слова на ленте находятся только пустые ячейки. Автомат находится в некотором состоянии из заданного множества и видит одну ячейку.

Задание работы машины Тьюринга можно описать программой – таблицей. В каждой клетке программы нужно указать, какие операции должен выполнить автомат, если, находясь в некотором состоянии, он "видит" данную букву. В общем случае, автомат, находясь в состоянии и обнаружив в ячейке букву , записывает в ту же ячейку заданную букву . Затем автомат выполняет движение , после чего переходит в состояние . Символ движения – это один из следующих трех символов: – автомат сдвигается на одну ячейку влево, – остается в той же ячейке, – сдвигается на одну ячейку вправо. Теперь следующее действие автомата нужно искать в строке, соответствующей состоянию , на пересечении со столбцом, соответствующим той букве, которую автомат "увидит" после сдвига. Считаем, что перед началом выполнения программы автомат находится в состоянии . В процессе своей работы машина Тьюринга будет как бы перескакивать из одной клетки программы в другую в соответствии с информацией на ленте и указаниями в клетках программы, пока не дойдет до клетки останова, в которой будет написано, что автомат должен оставить в очередной ячейке находящуюся там букву, остаться неподвижным и сохранить свое прежнее состояние. Клеток останова в программе может не быть; тогда машина Тьюринга никогда не остановится. Даже, если такие клетки есть, машина может никогда до них не дойти (ведь ее переходы зависят от программы и от входного слова). Если машина Тьюринга никогда не остановится, то считается, что она неприменима к данному входному слову. Она применима к слову только в том случае, если, начав работу над этим входным словом, рано или поздно дойдет до клетки останова.

Конфигурация машины Тьюринга представляет собой совокупность внутреннего состояния, состояния ленты, положения автомата на ленте. Конфигурацию машины Тьюринга будем записывать в виде , где – внутреннее состояние, – слово, находящееся слева от автомата, – слово, находящееся справа от автомата. Условимся считать, что стандартная начальная конфигурация имеет вид , а стандартная заключительная конфигурация имеет вид .

Машина Тьюринга правильно вычисляет частичную функцию , если для любого выполнено:

1. Если 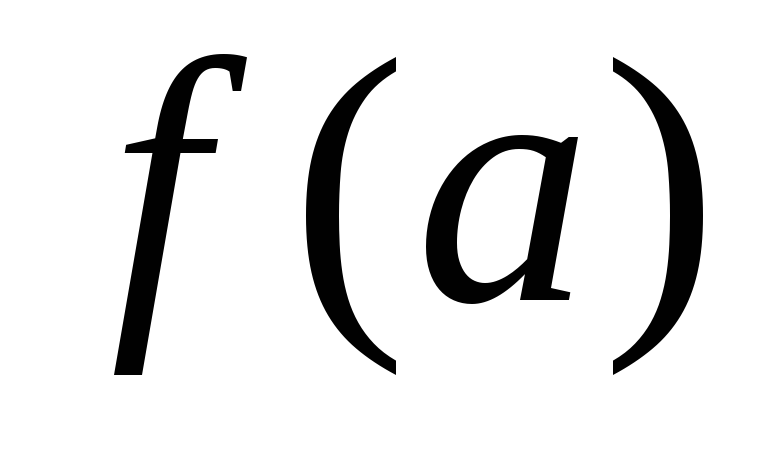определено и , то машина Тьюринга применима к начальной конфигурации 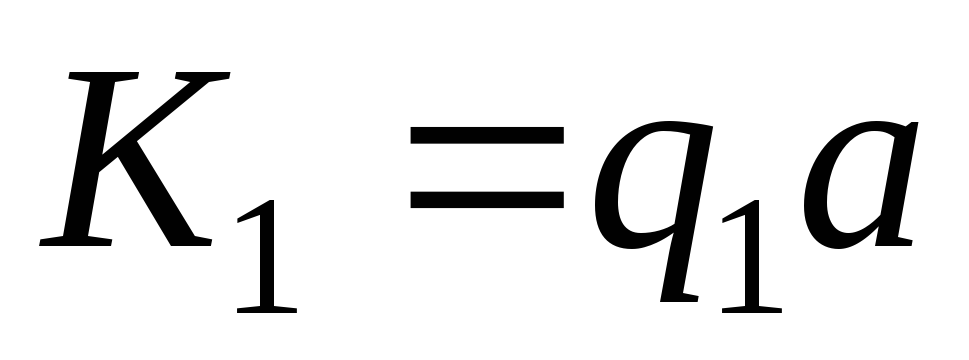и заключительной конфигурацией является .

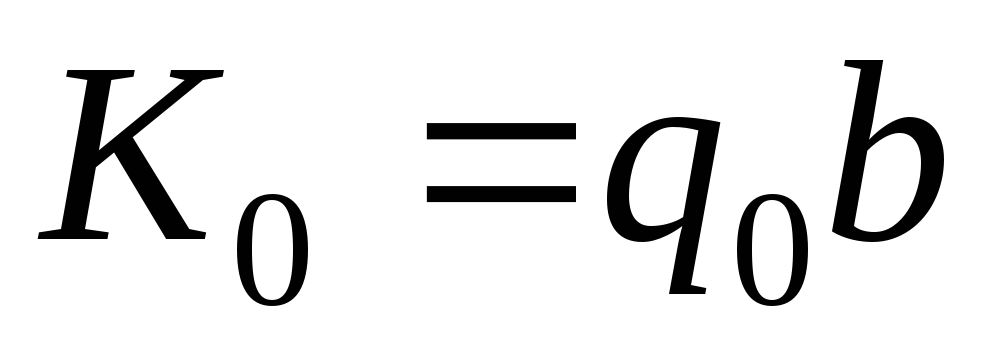2. Если не определено, то машина Тьюринга неприменима к начальной конфигурации .

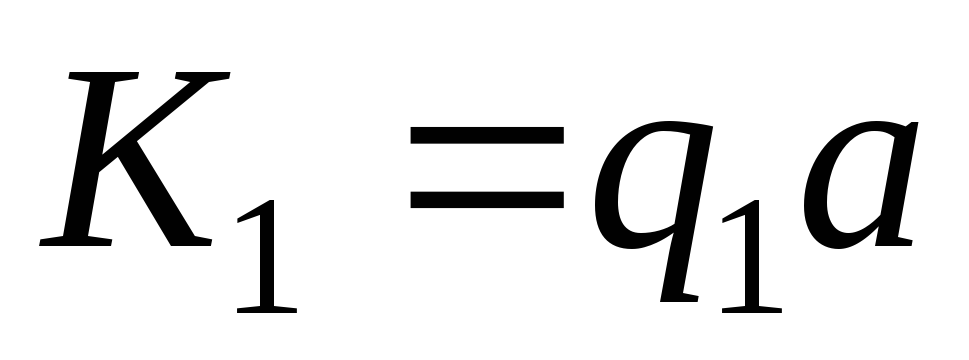Здесь – множество всех слов конечной длины в алфавите .

Функция называется правильно вычислимой по Тьюрингу, если существует машина Тьюринга, которая ее правильно вычисляет.

Пример машины Тьюринга, которая переводит начальную конфигурацию в заключительную конфигурацию .

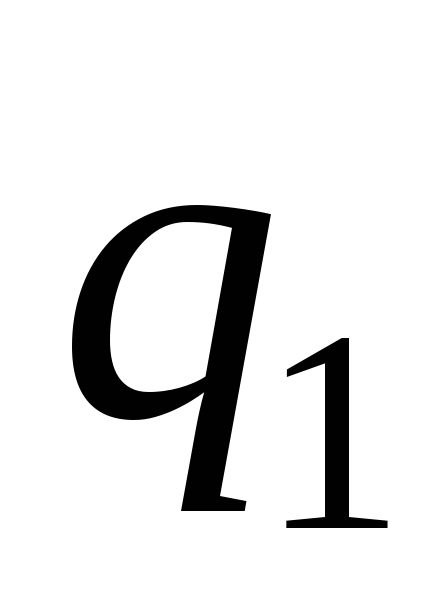
0
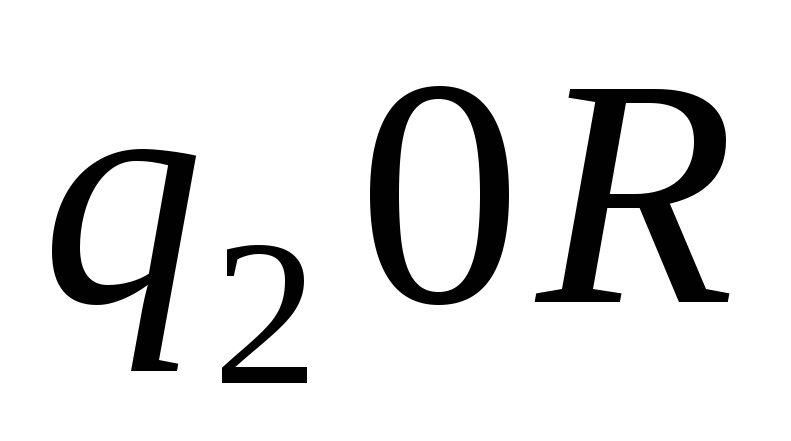
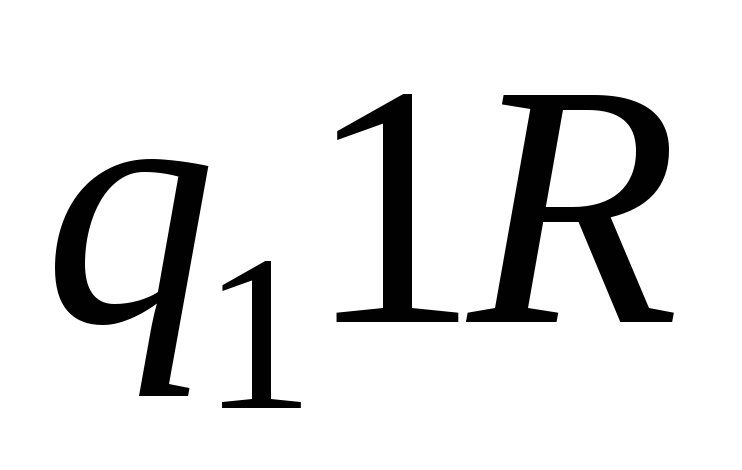
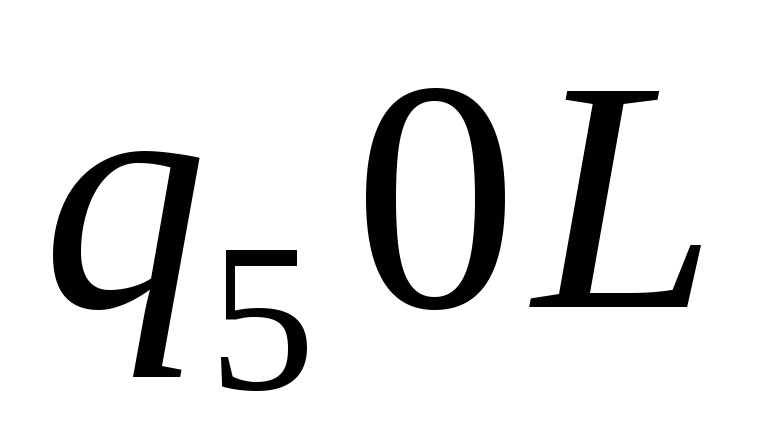
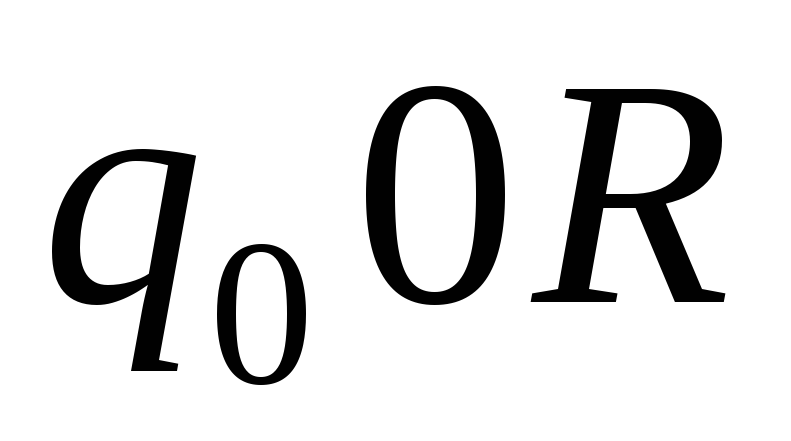
1

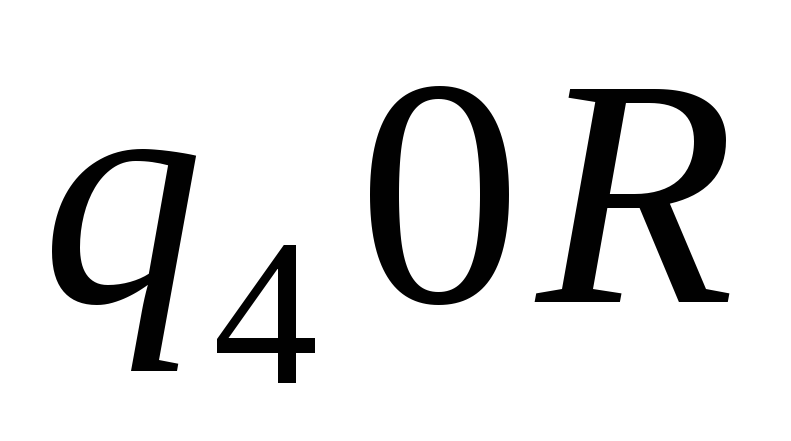
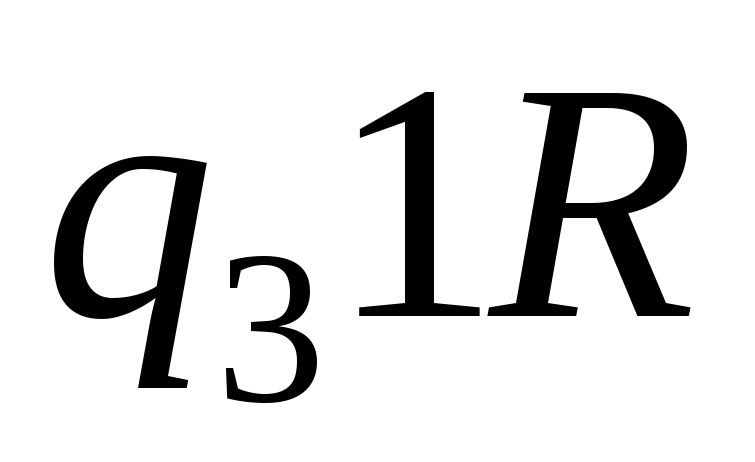
Описывая различные алгоритмы для машин и доказывая реализуемость всевозможных композиций алгоритмов, Тьюринг убедительно показал разнообразие возможностей предложенной им конструкции, что позволило выступить ему со следующим тезисом:

Тезис Тьюринга. Всякий алгоритм может быть реализован соответствующей машиной.

Этот тезис является формальным определением алгоритма. Он позволяет доказывать существование или отсутствие алгоритмов, описывая соответствующие машины Тьюринга или доказывая невозможность их построения. Доказать тезис Тьюринга нельзя, так как в его формулировке не определено понятие "всякий алгоритм", то есть левая часть тождества. Его можно только обосновать, представляя различные известные алгоритмы в виде машин Тьюринга. Дополнительное обоснование этого тезиса состоит в том, что позднее было предложено еще несколько общих определений понятия алгоритма и каждый раз удавалось доказать, что хотя новые алгоритмические схемы и выглядят иначе, они в действительности эквивалентны машинам Тьюринга: все, что реализуемо в одной из этих конструкций, можно сделать и в других. Эти утверждения доказываются строго, так как в них речь идет уже о тождественности формальных схем.

Нормальный алгоритм Маркова

В 1954 году советский математик А.А.Марков предложил другую алгоритмическую схему, эквивалентную машине Тьюринга, в которой данные преобразуются на основе других принципов. В алгоритмической схеме Маркова нет понятия ленты, и осуществляется непосредственный доступ к различным частям преобразуемого слова. Марков назвал эту алгоритмическую схему нормальным алгоритмом. Понятие нормального алгоритма, обладающее многими достоинствами как принципиального, так и методического характера, оказалось плодотворным и удобным. Выдержав испытание временем и доказав свою жизнеспособность, оно – наряду с понятиями рекурсивной функции и машины Тьюринга – прочно вошло в научный обиход современной теории алгоритмов.

Нормальный алгоритм Маркова представляет собой упорядоченный набор подстановок (продукций) вида

Формула подстановки служит для замены подслов в преобразуемом слове. Заменяемое и замещающееся подслова в формуле разделяются одной из стрелок → или • →. Продукция вида называется простой, а продукция – заключительной. В левой и правой частях формулы подстановки могут содержаться пустые слова. Для записи алгоритмов Маркова не требуется специального обозначения пустого слова, так как в этой конструкции носитель информации не зафиксирован, а преобразуемое слово свободно раздвигается и сдвигается. Заметим, что первое вхождение пустого слова находится слева от преобразуемого слова.

В качестве примера приведем алгоритм вычисления функции в алфавите (в алгоритме пустой символ обозначен как ):

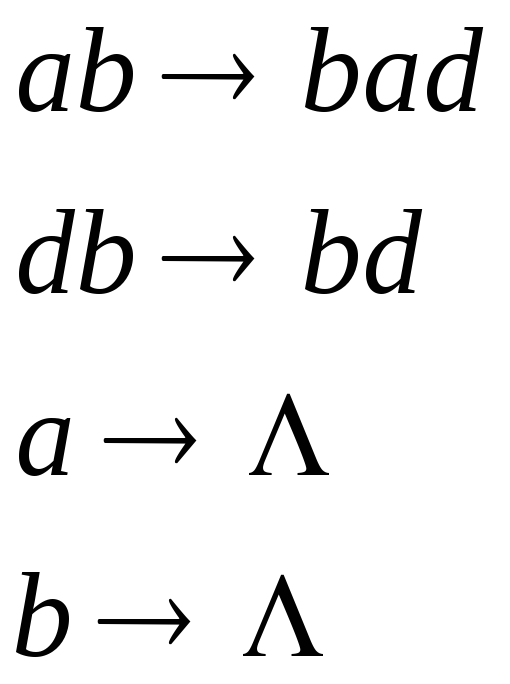
Выполнение алгоритма Маркова распадается на шаги. Каждый шаг включает в себя поиск первой по порядку формулы подстановки, применимой к преобразуемому слову, и выполнение, соответствующей этой формуле, замены. Если при попытке применить формулу подстановки оказывается, что имеется несколько вхождений ее заменяемой части, то всегда заменяется первое (самое левое) вхождение. Процесс выполнения алгоритма заканчивается в двух случаях:

– либо все формулы оказались неприменимыми,

– либо на последнем шаге была применена завершающая формула, в которой левое и правое подслова разделяет стрелка →.

В любом из этих случаев считается, что нормальный алгоритм применим к данному входному слову.

Если в процессе выполнения алгоритма бесконечное число раз применяются простые подстановки формулы, то алгоритм неприменим к данному входному слову.

Нормальный алгоритм называется нормальным алгоритмом над алфавитом , если он является нормальным алгоритмом в некотором расширенном алфавите . Нормальный алгоритм над алфавитом задает словарное отображение , используя в процессе обработки слов алфавита вспомогательные символы, не принадлежащие алфавиту . Остановка нормального алгоритма над алфавитом результативна, если алгоритм остановился с результатом , иначе будем считать результат работы алгоритма неопределенным.

Нормальный алгоритм вычисляет частичную функцию , если он каждое слово переводит в слово в случае, если или – неопределенно, если . Функция называется вычислимой по Маркову, если существует нормальный алгоритм Маркова ее вычисляющий.

Сравнивая алгоритмические схемы Тьюринга и Маркова, можно отметить, что у машины Тьюринга сравнительно развито управление при слабых возможностях преобразования информации, тогда как в алгоритмической схеме Маркова богаче возможности преобразования информации при менее развитом управлении. Авторы обеих алгоритмических схем старались простыми средствами обеспечить возможность описания любых алгоритмов. Тьюринг достиг этой цели в первую очередь за счет упрощения действия, а Марков – за счет упрощения логики управления.

Алгоритмические схемы Маркова и Тьюринга эквивалентны в том смысле, что все алгоритмы, описываемые в одной из них, могут быть описаны в другой. Эти схемы не могут быть физически реализованы, поскольку они являются математической абстракцией, допускающей неограниченно большую длину слов, возникающих в процессе преобразований.