Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Днепропетровский национальный университет им. Олеся Гончара

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

MTMO / ТЕОР_Я МАСОВОГО ОБСЛУГОВУВАННЯ

.pdf

Скачиваний:

Добавлен:

23.03.2015

Размер:

696.14 Кб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 55

буде нормально розподілена з параметрами 0 та 1. Звідси випливає, що

ui = ∑ri, j − 6 , j =1

де ri, j [0;1] – рівномірно розподілені псевдовипадкові числа.

Метод функціональних перетворень реалізує таку процедуру:

1)моделювання двох РРЧ ri,1, ri,2 [0;1] ;

2)обчислення пари нормально розподілених чисел

ui,1 = 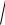−2 ln ri,1 sin (2πri,2 ) , ui,2 = 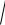−2 ln ri,1 cos (2πri,2 ) .

У такий спосіб можна одержати дві послідовності випадкових чисел

{ui,1;i = 1, N} та {ui,2 ;i = 1, N} .

Метод полярних координат також дозволяє моделювати одразу дві послідовності випадкових чисел ui шляхом:

1)моделювання двох РРЧ ri,1, ri,2 [0;1];

2)перетворення одержаних у п.1 чисел до РРЧ з інтервалу [−1;1] :

vi,1 = 2ri,1 −1, vi,2 = 2ri,2 −1;

3) обчислення

величини

= v2

+ v2

Якщо

s > 1,

то v

та v

i,1

i,2

i,1

i,2

ігнорують і

повертаються

до

п.

1. Якщо

si ≤ 1, то вважають,

що

точка

(vi,1, vi,2 ) є випадкова точка з одиничного кола, і переходять до п. 4;

4) обчислення випадкових чисел

= v

−2 ln si

= v

−2 ln si

i,1

i,2

Отже,

за

будь-яким

із

наведених

методів

може

бути

одержана

послідовність {ui ;i = 1, N} , а на її основі – послідовність {xi = m + σui ;i = 1, N} .

Зауваження 2. Двобічний квантиль нормального розподілу uα 2 можна визначити за формулою (4), якщо взяти ri = α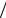2 .

Із нормальним розподілом тісно пов’язаний логарифмічно нормальний розподіл

		ln x−m
F ( x; m, σ) =	1	σ		−	y	2
	1	∫	exp		y		dy , x ³ 0 .
			exp				dy , x ³ 0 .
	2π			2
		−∞

Моделювання випадкових чисел для нього здійснюється за формулою

xi = exp ( yi ) ,

де yi N ( y; m, σ) – нормально розподілені числа з параметрами m та σ .

Оцінка якості випадкових чисел

Якість випадкових чисел можна оцінити двома способами:

1)відтворенням за одержаною послідовністю закону розподілу та перевіркою адекватності закону шляхом реалізації критеріїв згоди;

2)реалізацією спеціальних тестів для перевірки якості випадкових

чисел.

Наведені нижче тести призначені для перевірки якості

псевдовипадкових чисел, рівномірно розподілених на проміжку [0;1] .

Тест аперіодичності передбачає пошук такого номера i = i′ , після якого послідовність випадкових чисел повторюється. Шляхом перебору

здійснюється пошук номера i = i′ та	періоду L для послідовності чисел
r1, r2 ,…, rN , для яких виконується умова
ri′+ jL = ri′ , ri′+1+ jL = ri′+1 , …,	ri′+ p+ jL = ri′+ p , j = 1, 2,…

Якщо L < N , то порушується умова незалежності послідовності чисел r1, r2 ,…, rN і послідовність вважається неякісною.

Тест збігу моментів. Для рівномірно розподіленої випадкової

величини			ξ математичне сподівання дорівнює			E (ξ) =	1	, а	дисперсія

	1					2
D (ξ) =			Якщо послідовність {ri [0;1];i =		}
		.		1, N		являє собою			реалізацію

12			розподіленої випадкової величини ξ ,
рівномірно						то обчислена на її основі

статистична оцінка математичного сподівання, якою є середнє арифметичне

r = 1 ∑N ri , N i=1

має дорівнювати 1 , а статистична оцінка дисперсії

	1	N
s2 =		∑(ri −		)2
			r

	N −1 i=1

повинна становити 1 . 12

Застосовуючи тест збігу моментів, перевіряють гіпотезу щодо збігу теоретичних і статистичних моментів

Η0 : E (ξ) =		, D (ξ) = s2 ,	(5)
	r

для чого розглядають випадкові величини

ζ =		−	1	,	ζ		= s2	−	1	,
	r					2

1	2							12

які мають нормальні розподіли

ζ1	N (z1;0;σz ),	ζ2	N (z2	;0;σz	),
	1			2

де

	1				N 2	0,005 6		0,002 8		0,008 3
σ2z =		,	σ2z	=			+		−		.
						N		N 2		N 3
1	12N		2		N −1

Тоді процедура перевірки головної гіпотези (5) еквівалентна перевірці двох гіпотез:

Η0 : E (ζ1 ) = 0 ,

(6)

Η0 : D (ζ2 ) = 0 .

(7)

Для гіпотези (6) перевіряють умову

u =

ζ1

≤ u

(8)

12N

α 2

σz

де uα 2 – квантиль нормального розподілу.

Якщо умова (8) виконується, то підтверджується збіг математичного сподівання й середнього арифметичного.

Гіпотезу (7) перевіряють на основі умови

N -1

£ uα 2

(9)

sz2

0,0056N −1 + 0,0028N −2 - 0,0083N −3

виконання якої підтверджує збіг теоретичної й статистичної дисперсій. Якщо не виконується хоча б одна з нерівностей (8) або (9), генерована послідовність неякісна.

Тест коваріації призначений для перевірки незалежності елементів послідовності {ri ,i =1, N} на основі коваріаційної функції. Для цього

обчислюють коваріації поміж елементами послідовності, розташованими на відстані j одиниць один від одного:

C0 = cov{(r1, r2 ,…, rN ),(r1, r2 ,…, rN )} , C1 = cov{(r1, r2 ,…, rN −1 ),(r2 , r3 ,…, rN )} , C2 = cov{(r1, r2 ,…, rN −2 ),(r3 , r4 ,…, rN )} ,

…

C j = cov{(r1, r2 ,…, rN − j ),(rj+1, rj+2 ,…, rN )} .

Якщо (r1, r2 ,…, rN − j ) й (rj+1, rj+2 ,…, rN ) незалежні, то слушні рівності

		1	,	j = 0,
C j

	= 12
				j ³1.
	0,

Обчислення статистичного значення	ˆ	,	коли N > 50 , здійснюють за
	C j
спрощеною формулою:

N − j

∑

(ri - r )(ri+ j - r ) .

C j =

N - j

i=1

Якщо N ≤ 50 , застосовують точну формулу:

N − j

C j

∑ ri

∑rh ri+ j

∑rh+ j .

N - j

- j

i=1

h=1

N - j h=1

Головну гіпотезу щодо збігу теоретичних і статистичних коефіцієнтів

коваріації

j ³1,

H0 : C j = C j

приймають, якщо виконується умова

- C j

c juα 2

(10)

C j

N -

якщо j = 0,

де c j

якщо j ³1.

елементи {ri ;i =

}

"j ³1

Якщо

для

виконується

умова (10), то

1, N

незалежні, у противному разі вони залежні й послідовність неякісна.

Як максимальне значення j ³1 рекомендується брати 2/3 генерованої послідовності.

Якість послідовності випадкових чисел із розподілом F (x;Θ), де


Θ = {θ1,…, θs } , оцінюють таким					чином. Змодельовану		послідовність
{xi ;i =			} вважають
		1, N		якісною, якщо знайдені за		нею оцінки параметрів
ˆ	ˆ			параметрами	моделювання	θ1,…,θs ,	тобто правдиві
q1	,…,qs збігаються з

гіпотези

H0 : q j = qˆ j для "j =1, s .

Перевірка наведеної гіпотези ґрунтується на статистичних характеристиках

		ˆ
u j =	q j - q j			, j =		,
	q j - q j				1, s

		D (q j	)
		D (q j	)
		ˆ

які нормально розподілені. Якщо для заданої помилки першого роду α слушні нерівності

u j £ uα2 для "j =1, s ,

то послідовність можна вважати якісною.

Список рекомендованої літератури

Барлоу, Р. Математическая теория надежности [Текст] / Р. Барлоу, Ф. Прошан. – М.: Сов. радио, 1969. – 488 с.

Вентцель, Е.С. Теория случайных процессов и ее инженерные приложения [Текст] / Е.С. Вентцель, Л.А. Овчаров. – М.: Высш. шк., 2000. – 383 с.

Гнеденко, Б.В. Введение в теорию массового обслуживания [Текст] / Б.В. Гнеденко, И.Н. Коваленко. – М.: Наука, 1987. – 336 с.

Кокс, Л. Статистический анализ последовательностей событий [Текст] /

Л. Кокс, П. Льюис. – М.: Мир, 1969. – 312 с.

Кофман, А. Массовое обслуживание. Теория и приложения [Текст] / А. Кофман, Р. Крюон. – М.: Мир, 1965. – 302 с.

Потапов, В.Д. Имитационное моделирование производственных процессов в горной промышленности [Текст] / В.Д. Потапов, А.Д. Яризов. –

М.: Высш. шк., 1981. – 191 с.

Зміст

Передмова	3
Загальні вимоги до виконання лабораторних робіт	4
Лабораторна робота 1. Обробка потоку подій	5
Лабораторна робота 2. Моделювання одноканальної системи масового
обслуговування	19
Лабораторна робота 3. Моделювання багатоканальної системи масового
обслуговування	27
Додаток	33
Список рекомендованої літератури	44

<<< < Предыдущая 1 2 3 45 / 55

Соседние файлы в папке MTMO

#
23.03.2015194.05 Кб17TMO_LAB1.DOC
#
23.03.20151.33 Mб28Приставка О.П., Приставка П.О., Ємел'яненко Т.Г., Мацуга О.М. Випадков_ процеси (correct).pdf
#
23.03.2015696.14 Кб32ТЕОР_Я МАСОВОГО ОБСЛУГОВУВАННЯ.pdf