
MTMO / ТЕОР_Я МАСОВОГО ОБСЛУГОВУВАННЯ
.pdf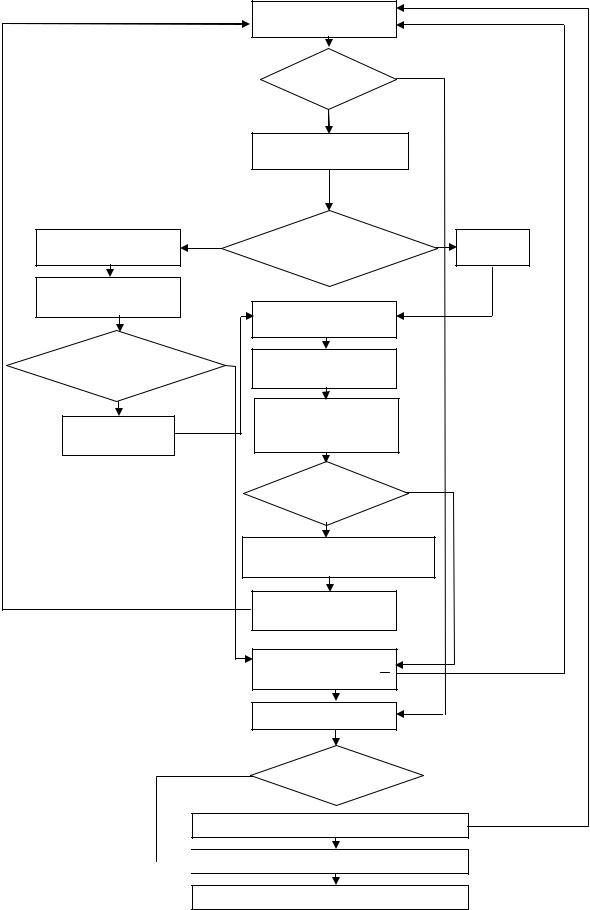
|
|
|
|
|
1. Формування t j |
|
|
|
|
||||
|
|
|
|
|
2. t j |
< T |
ні |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
так |
|
|
|
|
|
|
|
|
|
|
3. Вибір min t зв |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
lk |
|
|
|
|
5. Формування τч |
так |
4. t |
|
< min tзв |
ні |
п = t |
|
||||||
|
j |
9. t |
j |
||||||||||
|
|
|
j |
|
|
|
|
lk |
|
|
j |
||
6. tч = t |
j |
+ τч |
|
|
|
|
|
|
|
|
|
|
|
j |
|
j |
|
10. Формування τ j |
|
|
|
||||||
|
|
|
|
|
|
|
|
||||||
7. tч |
< min tзв |
так |
11. tзв = tп |
+ τ |
|
|
|
|
|||||
|
j |
|
|
|
|||||||||
j |
|
|
lk |
|
lk |
|
lk |
|
|
|
|
||
ні |
|
|
|
12. Збереження |
|
|
|
||||||
8. tпj |
= min tlkзв |
|
одержаного tlkзв |
|
|
|
|||||||
|
|
|
|
|
13. tзв < T |
ні |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
lk |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
так |
|
|
|
|
|
|
|
|
|
|
14. Лічильник кількості |
|
|
|
|||||
|
|
|
|
|
обслугованих вимог, m |
|
|
|
|||||
|
|
|
|
|
15. tп |
− t |
j |
|
|
|
|
||
|
|
|
|
|
|
|
j |
|
|
|
|
|
|
|
|
|
|
|
16. Лічильник |
m |
|
|
|
||||
|
|
|
|
|
кількості відмов, |
|
|
|
|||||
17. N + 1
ні
18. N < N*
 так
так
19. Перехід до чергової реалізації
 20. Обробка результатів моделювання
20. Обробка результатів моделювання
21. Видача результатів
Рис. 9. Блок-схема процесу моделювання багатоканальної СМО
30
Методичні рекомендації до виконання роботи
Створення програмного забезпечення необхідно виконувати з дотриманням таких вимог:
1.Параметри моделювання (параметри функцій розподілу, час функціонування, кількість та довжини черг; кількість приладів, періодичність збору статистики, кількість вимог, якщо необхідно) має задавати користувач.
2.Результат моделювання системи слід подати у вигляді календаря, що відображає її функціонування (табл. 13).
|
|
|
Таблиця 13 |
Календар роботи багатоканальної СМО |
|
||
Характеристики вимоги |
|
Номер вимоги |
|
|
1 |
… |
n |
Номер черги |
|
|
|
|
|
|
|
Номер приладу |
|
|
|
|
|
|
|
Момент часу надходження в |
|
|
|
систему |
|
|
|
Час перебування в черзі |
|
|
|
|
|
|
|
Момент часу надходження |
|
|
|
на прилад |
|
|
|
Час обслуговування |
|
|
|
|
|
|
|
Час перебування в системі |
|
|
|
|
|
|
|
Момент часу виходу з системи |
|
|
|
|
|
|
|
Результат обслуговування |
|
|
|
вимоги (обслугована чи ні) |
|
|
|
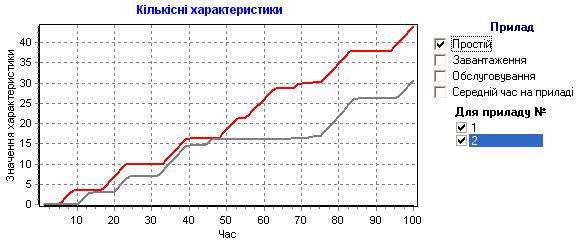
3. Зазначені в постановці задачі характеристики роботи системи необхідно подати у вигляді таблиці й графіків. Кількісні та ймовірнісні характеристики слід відображати на окремих графіках (рис. 10–13). Характеристики мають виводитися окремо для кожного приладу, кожної черги та всієї системи в цілому.
Рис. 10. Кількісні характеристики приладу багатоканальної СМО
31
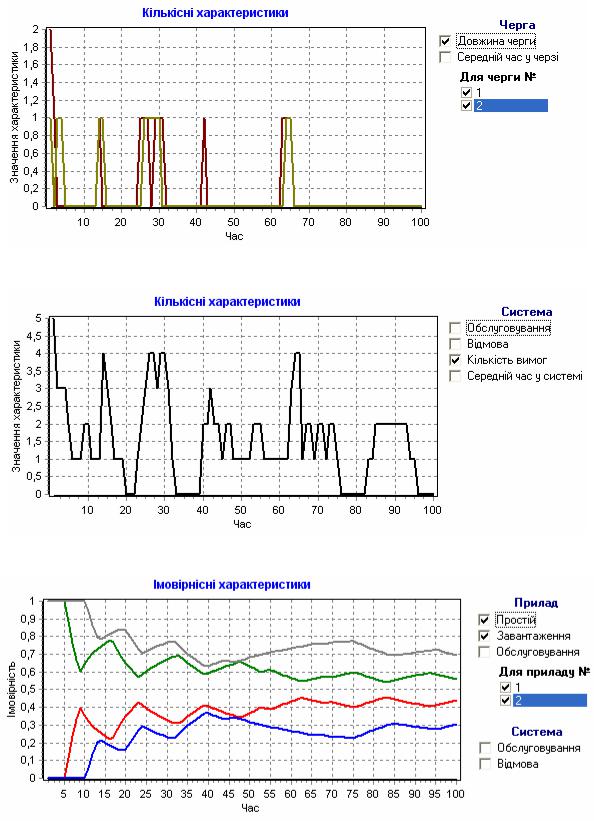
Рис. 11. Кількісні характеристики черги багатоканальної СМО
Рис. 12. Кількісні характеристики багатоканальної СМО
Рис. 13. Імовірнісні характеристики багатоканальної СМО
Створена програма має також задовольняти загальні вимоги.
32
Додаток Моделювання випадкових чисел
В інформаційному забезпеченні систем імітаційного моделювання систем масового обслуговування базові є процедури формування масивів реалізацій випадкових величин за заданим типом розподілу ймовірностей. При цьому розв’язання задачі формування таких масивів поділяється на два етапи. Спочатку здійснюється генерування так званих псевдовипадкових чисел ri [0;1] , що мають рівномірний розподіл, а далі – алгоритмічний
перехід до випадкових значень заданого типу розподілу.
Моделювання рівномірно розподілених випадкових чисел
Моделювання рівномірно розподілених чисел (РРЧ) може бути виконане за допомогою таблиць випадкових чисел, апаратним або програмним способом. Для реалізації на комп’ютері більш придатний програмний спосіб. Він полягає в тому, що РРЧ одержують за рекурентною формулою: кожне наступне число ri+1 утворюється з попереднього ri (або групи попередніх чисел) шляхом застосування алгебричних або логічних операцій:
ri +1 = f (ri ) .
Строго кажучи, така послідовність чисел не буде випадкова. Однак вона може задовольняти різні статистичні критерії випадковості. Тому ці числа використовують як випадкові й називають псевдовипадковими.
Головний недолік псевдовипадкових чисел – зациклювання. Тобто перші L послідовно одержаних псевдовипадкових чисел, починаючи з першого r1, будуть усі різні, а ( L +1) -ше псевдовипадкове число буде
збігатися з r1, ( L + 2) -ге – з числом r2 і т.д. Величина L називається періодом
псевдовипадкової послідовності. Він залежить від розрядності слова ЕОМ та методу формування псевдовипадкових чисел.
Усі розглянуті нижче алгоритми дозволяють одержувати цілі числа βi , що знаходяться в проміжку від нуля до m. Одержати ri [0;1] можна за співвідношенням
ri = βi . m
Один із перших алгоритмів одержання псевдовипадкових чисел на ЕОМ був запропонований Джоном фон Нейманом у 1946 р. Він називається методом середин квадратів і полягає в такому. Беруть довільне число, наприклад чотиризначне: β1 = 9 876 . Його підносять до квадрата й одержують
восьмизначне число β12 = 97 535 376 , із якого виділяють середні цифри. Ці середні цифри використовують як чергове випадкове число β2 = 5 353 і т.д.
33
Даний метод не дає задовільної послідовності випадкових чисел, розподіл одержаних за його допомогою чисел може відрізнятися від рівномірного. Крім того, одержана за його допомогою послідовність часто вироджується в нуль.
На сьогодні майже всі стандартні генератори псевдовипадкових чисел ґрунтуються на конгруентних алгоритмах, розроблених Д. Лемером у 1948 р. Лінійний конгруентний алгоритм задається формулою
|
βi+1 = (aβi + c) mod m , |
|
|
де m, a, c – |
цілі невід’ємні числа; 0 ≤ a, c < m ; |
β0 – |
початкове значення; |
( x) mod m – |
оператор модульної арифметики, |
який |
обчислює остачу від |
ділення цілого числа x на цілий модуль m.
Алгоритм називається конгруентним, оскільки використовує операцію «обчислення остачі» (у теорії чисел – одержання конгруентного числа). Якщо
c = 0 , |
конгруентний |
алгоритм |
називається мультиплікативним, а якщо |
c ¹ 0 |
– змішаним. |
й β0 слід |
|
|
Числа m, a, c |
обирати так, щоб забезпечити період L |
максимальної довжини та випадковість послідовності (друга умова не менш важлива, ніж перша, оскільки можна одержати датчик, що дозволяє генерувати послідовність із досить великим періодом, але не випадкову).
Оскільки βі – це остача від ділення на m, то 0 ≤ βі < m і кількість усіх можливих остач від 0 до m −1 дорівнює m. Тобто у псевдовипадковій послідовності може бути не більше ніж m різних значень ( L ≤ m ).
Виходячи з наведених міркувань, число m необхідно вибирати досить великим. Звичайно беруть m = pq , де p – основа системи числення, використовувана в ЕОМ (як правило, p = 2); q – кількість розрядів машини (наприклад, ). Оскільки L = m – це максимально можливий період, виникає питання, чи може бути досягнутий такий період і за яких значень величин m, a, c й β0. Відповідь дає нижченаведена теорема.
Теорема. Лінійна конгруентна послідовність, визначена числами m, a, c та β0, має період L = m тоді й тільки тоді, коли:
1)числа c і m взаємно прості;
2)число b = a −1 кратне k для кожного простого k, що є дільником m;
3)b кратне 4, якщо m кратне 4.
Із теореми випливає, що коли c = 0 , максимальний період не може бути досягнутий. Але за спеціальних умов можна досягти прийнятної довжини. Попри те що за c = 0 генеровані числа мають менший період, вважають, що мультиплікативний алгоритм працює швидше й дозволяє одержувати більш якісні послідовності.
Лінійні конгруентні алгоритми становлять основу багатьох обчислювальних процедур генерування псевдовипадкових чисел, наприклад:
rj +1 = 2−31β j +1 , β j +1 = (75β j )mod 231 ;
34
rj +1 = 10−11β j +1 , b j +1 = (74k +1b j )mod1011 ;
rj +1 = 10−10 β j +1 , b j +1 = (7b j ) mod1010 ;
rj +1 = 10−8β j +1 , b j +1 = (1 001b j + 231) mod108 ;
rj +1 = 2−32 β j +1 , b j +1 = (214 013b j + 2 531 011)mod 232 ;
rj +1 = 2−k β j +1 , b j +1 = (b2j + b j )mod 2k , k = 21.
Узагальненням лінійного конгруентного методу є квадратичний конгруентний метод:
b + = (db2 + ab + c)mod m .
i 1 i i
Наприклад, Р.Р. Ковей запропонував квадратичний конгруентний метод:
b + = (b2 + b )mod 2q , β0 mod 4 = 2 .
i 1 i i
Існує також адитивний конгруентний метод, що використовує формулу bi+1 = (bi + bi −1 ) mod m або bi+1 = (bi + bi−k ) mod m ,
де k – лаг, або запізнення.
Як показали теоретичні дослідження та результати комп’ютерних експериментів, дуже ефективним виявився адитивний генератор, розроблений Дж. Ж. Мітчеллом та Д.Ф. Муром:
bi+1 = (bi−24 + bi−55 ) mod m , |
i ³ 55 , |
де m – парне число.
Практично не поступається йому за якістю генератор, що його запропонував Дж. Марсалья:
bi+1 = (bi−24 ×bi−55 ) mod m , |
i ³ 55 . |
Інший важливий клас методів пов’язаний із комбінацією генераторів псевдовипадкових чисел. Припустимо, що наявні послідовності v0 ,v1,… та
w0 , w1,… випадкових чисел, які лежать між 0 та m −1, і ці послідовності
генеровані різними методами. Тоді можна, наприклад, використати одну випадкову послідовність для зміни порядку елементів іншої. Такий метод називається рандомізація перемішуванням. Відомі різні варіанти методів перемішування. Однак усі вони мають певний дефект. Вони змінюють порядок наступності генерованих чисел, але не самі числа. Здебільшого порядок наступності – це вирішальний фактор, але якщо початковий матеріал «недостатньо якісний», не рівномірно розподілений, то стан якості цих чисел після перемішування не зміниться. Тому деякі дослідники пропонують об’єднувати послідовність v0 ,v1,… та w0 , w1,… більш простим способом,
зокрема так:
bi = (vi - wi ) mod m .
35

Моделювання випадкових чисел окремих розподілів
Основний метод генерування неперервних випадкових чисел – метод оберненої функції. Нехай необхідно змоделювати випадкове число з
розподілу F ( x;Θ), де Θ = {θ1,…, θs } – вектор параметрів розподілу. Метод оберненої функції передбачає розв’язання рівняння
F ( xi ;Θ) = ri ,
де ri [0;1] – псевдовипадкові рівномірно розподілені числа. Розв’язуючи рівняння, одержують випадкові числа
xi = F −1 (ri ;Θ) ,
розподілені за потрібним законом.
Наприклад, для експоненціального розподілу
F ( x) = 1 − exp (−λx) ,
розв’язуючи рівняння
F ( xi ) = ri або 1 − exp (−λxi ) = ri ,
одержують формулу для генерування випадкових чисел: xi = − λ1 ln (1 − ri ) .
Нижче наводяться готові формули для моделювання випадкових чисел різних розподілів, одержані за методом оберненої функції (таблиця). Окремо розглянемо розподіли, для яких метод оберненої функції в явному вигляді не може бути застосований.
Для гамма-розподілу
F ( x) = γ (α,βx) , x ³ 0 ,
Γ (α)
випадкове число може бути згенероване на основі формули
α
xi = − 1 ∑ln (1 − ri, j ).
β j =1
Розподіл χ2 (Пірсона) з функцією розподілу
F ( x) = γ (ν(2, x )2) , x ³ 0 ,
Γ ν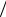 2
2
параметр якого ν називають степенем вільності, визначає випадкові числа, що генеруються як
|
|
|
|
|
|
|
|
3 |
|
|
|
|
2 |
|
|
2 |
|
|
|||
x ≈ ν 1 |
− |
|
+ u |
|
|
|
, |
(1) |
||
|
|
|||||||||
i |
|
|
9ν |
i |
9ν |
|
|
|||
|
|
|
|
|
|
|||||
де ui N (u;0,1) – випадкове число зі стандартного нормального розподілу.
36
Моделювання випадкових чисел окремих розподілів
Закон розподілу |
Функція розподілу |
Формула для моделювання |
|
випадкового числа |
|||
|
|
Експоненціаль- |
F ( x) = 1 − exp ( |
−λx) , x ³ 0 |
|
|
|
|
|
|
|
xi |
|
= − |
|
1 |
|
ln (1 − ri ) |
|
|
|||||||||||||||||||||||||||||||||||||
ний |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
λ |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Вейбулла |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
β |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 β |
|||||||
|
F ( x) = |
1 − exp |
− |
|
, |
|
x |
³ 0 |
|
|
|
|
|
|
|
xi |
|
= (−α ln (1 − ri )) |
|
|
|||||||||||||||||||||||||||||||||||
|
α |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Рівномірний |
F ( x) = |
|
x − a |
|
x [a;b] |
|
|
|
|
|
|
|
|
|
|
|
xi |
|
= a + ri (b − a) |
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
b − a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Релея |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= σ |
|
|
|
|
|
|
|
|
|
||||||||
F ( x) = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
−2 ln (1 − r ) |
|||||||||||||||||||||
|
1 − exp |
− |
|
|
|
|
|
|
|
, |
x |
³ 0 |
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2σ2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Парето |
F ( x) = |
|
|
|
|
k a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xi |
|
= k (1 − ri )1 a |
|
|
||||||||||||||||||||||||
|
1 − |
|
|
|
, x ³ k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
Лапласа |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
exp (λ ( x − μ)), − ∞ < x ≤ μ, |
|
|
|
|
|
|
|
|
|
ln (2ri ) + μ, |
xi ≤ μ, |
|||||||||||||||||||||||||||||||||||||
|
F ( x) = |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x = λ |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
1 |
|
ln (2(1 − ri |
)) + μ, xi > μ |
|||||||||||
|
|
|
|
1 |
− |
2 |
|
|
exp (−λ ( x − μ)),μ < x < ∞ |
|
− |
|
λ |
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Екстремальний |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x − m |
|
|
|
|
|
|
|
|
xi |
|
= m − σ ln (− ln (ri )) |
||||||||||||||||||||||
(найбільшого |
F ( x) = exp |
− exp |
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
σ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
значення) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Із класу |
F ( x) = 1 − exp ( |
− (exp (Bx |
β |
) −1)) |
|
|
|
|
|
1 |
|
|
|
|
1 β |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
екстремальних |
|
|
|
xi |
|
= |
|
|
|
|
|
|
ln (1 − ln (1 |
− ri )) |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
B |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Розподіл Стьюдента, функція щільності якого має вигляд |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
f ( x) = |
|
Γ ((ν + 1) 2)(1 + x2 ν)−(ν+1) 2 |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
νπΓ (ν 2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
а параметр ν називають степенем вільності, визначає процедуру генерування |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
випадкових чисел типу |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
x ≈ u + |
1 |
g |
|
(u ) + |
|
|
|
1 |
|
g |
|
|
(u |
) + |
1 |
|
g |
|
(u ) + |
|
1 |
g |
|
|
|
(u ) , |
(2) |
|||||||||||||||||||||||||||
|
|
|
|
ν2 |
|
|
|
ν3 |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
де ui N (u;0,1) |
i i |
|
|
|
ν |
|
|
1 i |
|
|
|
|
|
|
2 |
|
i |
|
|
3 |
i |
|
ν4 |
|
|
|
4 |
|
i |
|
|
||||||||||||||||||||||||
– випадкове число зі стандартного нормального розподілу; |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
g1 (ui ) = |
1 |
(ui3 + ui |
); |
|
|
|
|
|
|
|
|
|
g2 |
(ui |
) = |
1 |
|
(5ui5 + 16ui3 + 3ui ); |
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
96 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
g3 (ui ) = |
|
1 |
|
(3ui7 + 19ui5 + 17ui3 −15ui ); |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
384 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
g4 |
(ui ) = |
|
1 |
|
|
|
|
|
(79ui9 + 779ui7 +1 482ui5 −1 920ui3 − 945ui ). |
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
92 160 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
37

Для розподілу Фішера з функцією щільності
|
Γ |
ν1 |
+ ν2 |
|
|
|
|
|
ν1 |
ν −2 |
|
|
|
|
|
− |
ν1 +ν2 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
f ( x) = |
|
|
|
2 |
|
|
|
|
ν |
2 |
1 |
|
|
ν |
|
2 |
|
||||||
|
|
|
|
|
|
|
|
+ |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
x |
2 |
1 |
|
1 |
x |
|
|
, x ³ 0 , |
||
|
ν |
|
|
|
ν |
|
|
|
ν |
|
ν |
|
|||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
Γ |
1 |
|
Γ |
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
||||||
|
2 |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
де ν1 , ν2 – параметри |
розподілу, |
що їх називають |
степенями вільності, |
||||||||||||||||||||||||||||||||||||||
випадкові числа можуть бути одержані зі співвідношення |
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xi |
= exp (2zi ) , |
|
|
|
|
|
|
|
|
|
|
|
|
(3) |
|||||||
де |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
σ |
σ |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
||||||
|
|
zi = ui |
σ − |
δ (ui2 + 2) + |
|
|
|
|
|
(ui2 + 3ui ) + |
|
δ |
|
(ui3 + 11ui ) − |
|||||||||||||||||||||||||||
|
|
|
|
|
2 |
24 |
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
2 |
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
72 σ |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(ui4 + 9ui2 + 8)+ |
|
|
3 |
|
|
(3ui4 + 7ui2 |
−16) + |
|
|
|
|
|
|
|
|
|
|
2 |
|
(ui5 + 20ui3 + 15ui ) + |
|||||||||||||||||||
|
δσ |
|
|
|
|
|
|
σ |
|
|
σ |
|
|||||||||||||||||||||||||||||
− |
|
δ |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
3 240σ |
|
|
2 |
|
1 920 |
|||||||||||||||||||||||||||||||||||
120 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
δ4 |
( i |
|
|
|
|
i |
|
|
|
|
i ) |
|
|
|
|
δ4 |
2 |
( |
|
|
i |
|
|
|
|
|
|
|
|
i |
i |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
) |
||||||||||||||
+ |
2 880 |
u5 |
+ 44u3 |
+ 183u |
|
|
+ |
155 520σ |
|
|
|
9u5 |
− 284u3 |
−1 513u |
; |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
σ = |
1 |
|
+ |
1 |
|
; |
|
δ = |
|
|
1 |
|
− |
|
1 |
; |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
ν |
|
ν |
|
|
|
|
|
ν |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
ν |
2 |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
де ui N (u;0,1) – |
випадкове число зі стандартного нормального розподілу. |
||||||||||||||||||||||||||||||||||||||||
Зауваження 1. Наведені вище вирази можуть бути застосовані для |
|||||||||||||||||||||||||||||||||||||||||
визначення квантилів χ2 |
|
, |
t |
|
, |
|
|
f |
α,ν ,ν |
розподілів χ2 , |
Стьюдента й Фішера |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
α,ν |
|
α,ν |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
відповідно. Для цього у формулах (1) і (3) необхідно ui замінити на однобічний квантиль нормального розподілу u1−α , а у формулі (2) – двобічний квантиль нормального розподілу на uα 2 .
Моделювання нормально розподілених випадкових чисел
Моделювання випадкових чисел із нормальним розподілом
N ( x; m, σ) = |
1 |
x |
|
|
− |
( y − m)2 |
|||
|
|
∫ |
exp |
|
|
2 |
|
||
|
|
|
|||||||
σ 2π |
|
2σ |
dy |
||||||
|
−∞ |
|
|
|
|
|
|||
здійснюється за формулою
xi = m + σui ,
де ui – випадкове число зі стандартного нормального розподілу N (u;0,1) .
Тобто задача зводиться до моделювання нормально розподілених випадкових чисел не з довільними параметрами m і σ , а з параметрами 0 і 1.
38

Існує низка методів генерування ui . Одим з основних є метод оберненої функції, який передбачає розв’язання рівняння
ui
де 
 12π −∞∫
12π −∞∫
|
F (ui ; 0,1) = ri |
|
|
|||
|
|
y |
2 |
|
|
|
exp |
− |
|
dy = Φ (u |
) |
||
|
|
|||||
|
2 |
|
i |
|
||
|
|
|
|
|||
|
|
1 |
|
ui |
|
|
y2 |
|
|
або |
|
|
|
∫ |
exp |
− |
|
dy = r , |
|
|
|
|
|
||||||
|
|
2π |
|
|
|
2 |
|
i |
|
|
|
|
|
−∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|||
– функція Лапласа.
Розв’язком даного рівняння є число
ui = Φ−1 (ri ) ,
для обчислення якого застосовують апроксимаційні функції. Якщо ri ≤ 0,5 , то
|
|
|
u = Φ−1 |
(r ) ≈ |
c |
|
+ c t + c t2 |
− t , |
|
|
|||||||
|
|
|
0 |
|
|
1 |
|
2 |
|
|
|
|
|
||||
|
|
|
1 + d t + d |
|
t2 + d t3 |
|
|
||||||||||
|
|
|
i |
i |
2 |
|
|
|
|
||||||||
|
|
|
|
|
1 |
|
|
|
3 |
|
|
|
|
|
|||
де |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
t = |
|
; |
c0 = 2,515 517 ; |
|
|
c1 = 0,802 853 ; |
|
c2 = 0, 010328 ; |
|||||||||
−2 ln (ri ) |
|
|
|
||||||||||||||
|
d1 = 1, 432 788 ; |
d2 = 0,189 265 9 ; |
|
d3 = 0, 001 308 . |
|||||||||||||
Якщо ri > 0,5 , то має місце співвідношення |
|
|
|
|
|
|
|||||||||||
|
|
|
u = Φ−1 (r ) ≈ t − |
|
|
c |
|
+ c t + c t |
2 |
|
|
||||||
|
|
|
|
|
0 |
1 |
|
2 |
|
|
, |
(4) |
|||||
|
|
|
|
|
+ d t + d |
|
t2 + d t3 |
||||||||||
|
|
|
i |
i |
|
1 |
2 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
3 |
|
|
|
де t = 
 −2 ln (1 − ri ) .
−2 ln (1 − ri ) .
Інший є метод додавання, в основі якого лежить центральна гранична теорема. Згідно з нею у випадку складання великої кількості випадкових величин з однаковими дисперсіями одержана випадкова величина буде асимптотично розподілена за нормальним законом.
Дослідження показали, що в разі складання 12 випадкових величин
|
|
|
|
12 |
||||
Ri [0;1] , рівномірно розподілених на проміжку [0;1] , їх добуток V = ∑Ri |
||||||||
|
|
|
|
|
|
|
i=1 |
|
буде нормальною величиною з параметрами |
|
|
|
|
||||
|
12 |
|
12 |
|
1 |
|
|
|
E (V ) = E |
∑Ri |
|
= ∑E (Ri ) = 12 |
|
= 6 , |
|||
2 |
||||||||
|
|
|
i =1 |
|
|
|||
i=1 |
|
|
|
|
|
|||
|
12 |
|
12 |
|
1 |
|
||
D (V ) = D |
∑Ri |
|
= ∑D (Ri ) = 12 |
|
= 1. |
|||
12 |
||||||||
|
|
|
i=1 |
|
||||
i=1 |
|
|
|
|
|
|||
Якщо пронормувати величину V , то одержана величина
U = V − E (V ) = V − 6
D (V )
39
