Эта формула называется формулой Торричелли.

Итак, скорость истечения жидкости из отверстия, расположенного на глубине h под открытой поверхностью, совпадает со скоростью, которую приобретает любое тело, падая с высоты h. Следует помнить, что этот результат получен в предположении, что жидкость идеальна. Для реальных жидкостей скорость истечения будет меньше, причем тем сильнее отличается от значения (55.5), чем больше вязкость жидкости.

§56. Измерение давления в текущей жидкости

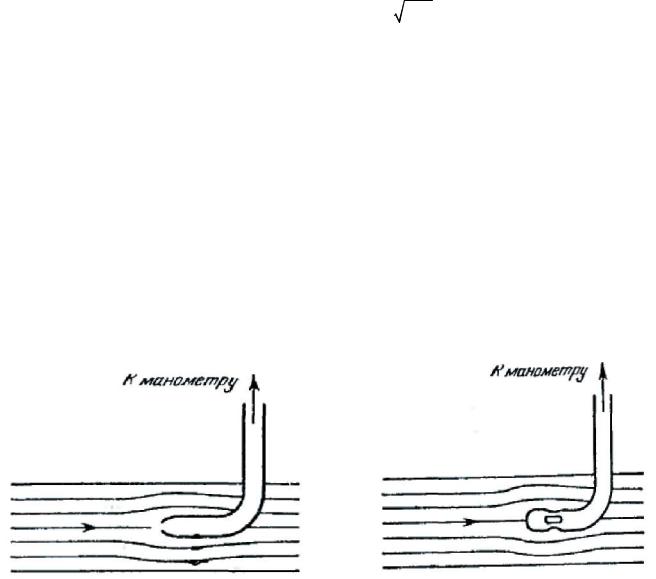
В предыдущем параграфе мы выяснили, что давление в жидкости связано с величиной скорости течения. Введение в жидкость прибора для измерения давления нарушает характер движения жидкости, а следовательно, может изменить и величину измеряемого давления. Поместим в жидкость изогнутую манометрическую трубку с входным отверстием, обращенным навстречу потоку (рис. 148). Такую трубку называют трубкой Пито. Рассмотрим линию тока, упирающуюся своим концом в центр отверстия трубки. Скорость вдоль рассматриваемой линии тока будет изменяться от υ для невозмущенного потока на больших расстояниях от трубки до нуля непосредственно перед отверстием. Согласно уравнению Бернулли давление перед отверстием

Рис 148 Рис. 149 (а следовательно, и в манометрической трубке) будет превышать давление в невозмущенном

потоке р на величину ρυ 2 / 2 . Следовательно, манометр, соединенный с трубкой Пито, покажет давление, равное

динамического давлений, называется полным давлением. Таким образом, с помощью трубки Пито можно измерять полное давление (56.1).

Если в тонкой изогнутой трубке сделать боковые отверстия, то скорость (а следовательно, и давление) вблизи таких отверстий будет мало отличаться от скорости (и давления)

152

невозмущенного потока (рис. 149), Поэтому манометр, присоединенный к такой трубке, называемой зондом, покажет статическое давление в жидкости p.

Зная полное и статическое давления, можно найти динамическое давление ρυ 2 / 2 , а следовательно, и скорость течения υ (плотность жидкости предполагается известной). Если трубку Пито и зонд смонтировать вместе, как показано на рис. 150, и подсоединить к разным коленам дифференциального манометра (т. е. манометра, измеряющего разность давлений), то показания манометра будут непосредственно давать динамическое давление. Проградуировав манометр в значениях скорости υ , можно получить прибор для измерения скорости течения жидкости.

Рис. 150

§57. Применение к движению жидкости закона сохранения импульса

К жидкостям и газам, как и к другим телам, применим закон сохранения импульса. Используем этот закон для решения некоторых задач.

Реакция текущей жидкости на стенки изогнутой трубы. Предположим, что в изогнутой трубе установился стационарный поток несжимаемой жидкости (рис. 151). Для простоты возьмем трубу постоянного сечения S. Тогда в силу неразрывности струи скорость в каждом сечении будет одинакова по величине и равна υ .

Рис. 151

Рассмотрим объем изогнутого участка трубы, ограниченного сечениями S1 и S2. За время t в этот объем будет втекать через сечение S1 количество жидкости Sυ t , обладающее

импульсом1 K1 = ρ Sυv1 t . Одновременно из этого объема будет вытекать через сечение S2

1 Давление обозначается той же буквой р, что и импульс. Поэтому в случаях, когда могут возникнуть недоразумения, мы будем обозначать именно буквой К.

153

такое же количество жидкости, обладающее импульсом K2 = ρ Sυv2 t . Таким образом, стенки изогнутого участка трубы сообщают за время t текущей мимо них жидкости приращение

времени равно действующей на тело силе. Следовательно, стенки трубы действуют на жидкость

Силу fr называют реакцией текущей жидкости на стенки трубы.

Реакция вытекающей струи. Струя жидкости, вытекающая из отверстия в сосуде (рис. 152),

уносит с собой за время t импульс K = ρ Sυv t ( ρ — плотность жидкости, S — площадь отверстия, v — скорость истечения струи). Этот импульс сообщается вытекающей жидкости

Рис. 152

Эта сила называется реакцией вытекающей струи. Если сосуд поставить на тележку, то под действием силы fr он придет в движение в направлении, противоположном направлению струи.

Найдем величину силыfr, воспользовавшись выражением (55.5) для скорости истечения жидкости из отверстия:

Если бы, как это может показаться на первый взгляд, сила fr совпадала по величине с силой гидростатического давления, которое жидкость оказывала бы на пробку, закрывающую отверстие, то fr была бы равна ghpS.

На самом деле сила fr оказывается в 2 раза большей. Это объясняется тем, что возникающее при вытекании струи движение жидкости в сосуде приводит к перераспределению давления, причем давление вблизи стенки, лежащей против отверстия, оказывается несколько большим, чем вблизи стенки, в которой сделано отверстие.

На реакции вытекающей струи газа основано действие реактивных двигателей и ракет. Реактивное движение, не нуждаясь для своего осуществления в наличии атмосферы, используется для полетов в космическое пространство.

Основоположником теории межпланетных сообщений является выдающийся русский ученый и изобретатель К Э. Циолковский (1857—1935). Он дал теорию полета ракеты и обосновал возможность применения реактивных аппаратов для межпланетных сообщений. В частности, Циолковским была разработана теория движения составных ракет, в которых каждая последующая ступень вступает в действие после того, как предыдущая ступень, израсходовав

154

полностью топливо, отделится от ракеты. Идеи Циолковского получили дальнейшее развитие и были осуществлены советскими учеными и инженерами, обеспечившими ведущую роль Советского Союза в освоении и изучении космического пространства,

§58. Силы внутреннего трения

Идеальная жидкость, т. е. жидкость без трения, является абстракцией. Всем реальным жидкостям и газам в большей или меньшей степени присуща вязкость или внутреннее трение. Вязкость проявляется в том, что возникшее в жидкости или газе движение после прекращения действия причин, его вызвавших, постепенно прекращается.

Для выяснения закономерностей, которым подчиняются силы внутреннего трения, рассмотрим следующий опыт. В жидкость погружены две параллельные друг другу пластины (рис. 153), линейные размеры которых значительно превосходят расстояние между ними d. Нижняя пластина удерживается на месте, верхняя приводится в движение относительно нижней

с некоторой скоростью υ0 . Опыт дает, что для перемещения верхней пластины с постоянной

скоростью υ0 необходимо действовать на нее с вполне определенной постоянной по величине силой f. Раз пластина не получает ускорения, значит, действие этой силы уравновешивается равной ей по величине противоположно направленной силой, которая, очевидно, есть сила трения, действующая

Рис. 153.

на пластину при ее движении в жидкости. Обозначим ее fтр.

Варьируя скорость пластины υ0 площадь пластин S и расстояние между ними d, можно получить, что

где η — коэффициент пропорциональности, зависящий от природы и состояния (например, температуры) жидкости и называемый коэффициентом внутреннего трения или коэффициентом вязкости, или просто вязкостью жидкости (газа).

Нижняя пластина при движении верхней также оказывается подверженной действию силы

Таким образом, при движении двух погруженных в жидкость пластин друг относительно друга между ними возникает взаимодействие, характеризуемое силой (58.1). Воздействие пластин друг на друга осуществляется, очевидно, через жидкость, заключенную между пластинами, передаваясь от одного слоя жидкости к другому. Если в любом месте зазора провести мысленно плоскость, параллельную пластинам (см. пунктирную линию на рис. 153), то можно утверждать. Что часть жидкости, лежащая над этой плоскостью, действует на часть

155

в свою очередь действует на часть жидкости, лежащую над плоскостью, с силой fò ð , причем

величина fò ð и fò ð′ определяется формулой (58.1). Таким образом, формула (58.1) определяет не только силу трения, действующую на пластины, но и силу трения между соприкасающимися частями жидкости.

Если исследовать скорость частиц жидкости в разных слоях, то оказывается, что она изменяется в направлении z перпендикулярном к пластинам (рис. 153), по линейному закону

Частицы жидкости, непосредственно соприкасающиеся с пластинами, как бы прилипают к ним и имеют такую же скорости как и сами пластины, Согласно формуле (58.2)

Использовав равенство (58.3), формуле (58.1) для силы внутреннего трения можно придать вид

dυ

Величина dz показывает, как быстро изменяется скорость в направлении оси z, и называется градиентом скорости (точнее, это—модуль градиента скорости; сам градиент — вектор).

Формула (58.4) была нами получена для случая, когда скорость изменяется по линейному закону (в этом случае градиент скорости является постоянным). Оказывается, что эта формула остается справедливой и для любого другого закона изменения скорости при переходе от слоя к

слою. В этом случае для определения силы трения между двумя граничащими друг с другом dυ

слоями нужно брать значение градиента dz в том месте, где проходит воображаемая поверхность раздела слоев. Так, например, при движении жидкости в круглой трубе скорость равна нулю у стенок трубы, максимальна на оси трубы и, как можно показать, при не слишком больших скоростях течения изменяется вдоль любого радиуса по закону

где R — радиус трубы, υ0 — скорость па оси трубы, υ — скорость на расстоянии z от оси трубы (рис. 154). Проведем в жидкости мысленно цилиндрическую поверхность радиуса r Части жидкости, лежащие по разные стороны от этой поверхности, действуют друг на друга с силой, величина которой в расчете на единицу поверхности равна

f = η dυ = η 2υ0r dr R2

т, е. возрастает пропорционально расстоянию поверхности раздела от оси трубы (знак «—», получающийся при дифференцировании (58.5) по r, мы опустили, поскольку формула (58.4) дает лишь модуль силы внутреннего трения).

156