
AGLA
.pdf
(
i утворює кут π/3 з прямою
x = y, z = 0;
б) проходить через пряму
(
x + 5y + z = 0, x − z + 4 = 0
i утворює кут π/4 з площиною x − 4y − 8z + 1 = 0.
7Нормальне рiвняння прямої на площинi. Нормальне рiвняння площини в просторi
Вцьому роздiлi використовуються такi поняття та результати.
1.Нормальне рiвняння прямої на площинi. Знаходження вiдхилення i вiдстанi вiд точки до прямої. Положення точки вiдносно прямої на площинi.
2.Нормальне рiвняння площини в просторi. Знаходження вiдхилення i вiдстанi вiд точки до площини. Положення точки вiдносно площини в просторi.
Приклади розв’язання задач
Приклад 7.1. Знайти вiдхилення δ i вiдстань d вiд точки M (2, 5) до прямої γ : 8x − y + 2 = 0. В однiй чи в рiзних пiвплощинах вiдносно γ лежать початок координат i точка M ?
Розв’язання. Запишемо нормальне рiвняння прямої γ. Нагадаємо, для того, щоб звести загальне рiвняння прямої Ax + By + C = 0 до нормального, необхiдно це рiвняння домножити справа i злiва на нормуючий
− sign C
множник µ = √A2 + B2 (тут вважаємо, що sign 0 = 1):
|
Ax + By + C |
|
||
µAx + µBy + µC = 0 або − sign C |
√ |
|
|
= 0. |
A2 + B2 |
||||
81

 O M
O M
γ d
d
−1
В нашiй ситуацiї µ = √ , нормальне рiвняння прямої
65 |
|
|
|
|
|
|
|
γ : −√8 |
x + |
1 |
y − |
2 |
= 0. |
||
√ |
|
√ |
|
||||
65 |
65 |
65 |
|
||||
Для того, щоб знайти δ вiдхилення вiд точки M до прямої γ, необхiдно в нормальне рiвняння прямої замiсть змiнних x, y пiдставити координати точки M :
δ = |
−8 |
2 + |
1 |
|
5 |
2 |
= |
1 . |
|||||||
|
√ |
|
· |
|
√ |
|
· |
|
− |
√ |
|
|
−√ |
|
|
|
|
65 |
|
|
65 |
|
|
65 |
|
5 |
|
||||
Нагадаємо, що вiдхилення це вiдстань вiд точки до прямої, взята iз знаком ”+”, якщо дана точка i початок координат лежать в рiзних пiвплощинах вiдносно заданої прямої, iз знаком ”–”, якщо в однiй.
1
Таким чином, вiдстань вiд точки M до γ дорiвнює d = |δ| = √ .
5
Точка M i початок координат лежать в однiй пiвплощинi вiдносно γ, оскiльки δ < 0.
Приклад 7.2. Задана пряма γ : Ax + By + C = 0 i точки M (x1, y1) ,
N (x2, y2) , якi не належать γ, тобто Axi +Byi +C =6 0, i = 1, 2. Визначити необхiдну i достатню умову того, що
а) γ перетинає вiдрiзок M N ;
б) γ перетинає продовження вiдрiзку M N за точку M.
Розв’язання. Позначимо через δ1 i δ2 вiдхилення вiд точок M i N до прямої γ, вiдповiдно. Нагадаємо, що
|
Axi + Bxi + C |
|
||
δi = − sign C |
√ |
|
|
, i = 1, 2. |
A2 + B2 |
||||
82

N
γ |
O |
M
Для того, щоб пряма γ перетинала вiдрiзок M N, необхiдно i достатньо, щоб точки M i N лежали в рiзних пiвплощинах вiдносно γ. Нехай γ не проходить через початок координат (C =6 0). Тодi можливi двi ситуацiї: або M i початок координат лежать в однiй пiвплощинi вiдносно γ, а точка N в iншiй (тобто δ1 < 0 i δ2 > 0), або, навпаки, N i початок координат лежать в однiй пiвплощинi вiдносно γ, а точка M в iншiй (тобто δ1 > 0 i δ2 < 0). Таким чином, пряма γ перетинає вiдрiзок M N тодi i тiльки тодi, коли числа δ1 i δ2 мають рiзнi знаки: δ1δ2 < 0. Маємо,
|
δ1δ2 = |
(sign C)2 |
|
||
|
|
|
(Ax1 + By1 + C) (Ax2 + By2 + C) . |
|
|
|
A2 + B2 |
|
|||
|
(sign C)2 |
|
|||
Оскiльки, |
|
> 0, то умова δ1δ2 < 0 еквiвалентна такiй: |
|
||
A2 + B2 |
|
||||
|
(Ax1 + By1 + C) (Ax2 + By2 + C) < 0. |
(1) |
|||
Зауважимо, що така ж сама умова справедлива i в тому випадку, коли пряма γ проходить через початок координат (тодi C = 0). Дiйсно, в цiй ситуацiї, для того, щоб пряма γ перетинала вiдрiзок M N необхiдно i достатньо, щоб проекцiї радiус-векторiв точок M i N (позначимо їх ~r1 i ~r2, вiдповiдно) на вектор нормалi до γ (позначимо його ~n) мали б рiзнi знаки: Πp~n ~r1 Πp~n ~r2 < 0. Оскiльки, ~r1 = {x1, y1} , ~r2 = {x2, y2} ,
|
|
|
n |
M |
|
|
|
|
|
|
|
|
||
|
|
|
γ |
|
|
r1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
O |
|
|
|
|
|
|||
|
|
|
|
r |
|
|
|
|
|
|||||
|
|
N |
|
|
|
|
|
|
|
|
||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||
~n = {A, B} , тодi |
( ~r1, ~n ) |
|
( ~r2, ~n ) |
Ax1 + By1 |
|
Ax2 + By2 |
|
|||||||
|
|
|
|
|||||||||||
Πp~n ~r1 · Πp~n ~r2 = |
|
· |
|
|
|
= |
√ |
|
|
· |
√ |
|
|
< 0. |
|~n | |
|
|~n | |
|
|
|
|
|
|||||||
|
|
A2 + B2 |
A2 + B2 |
|||||||||||
83

Враховуючи, що знаменник завжди додатний, маємо умову (1). Таким чином, γ перетинає вiдрiзок M N, якщо виконується (1).
Для того, щоб пряма γ перетинала продовження вiдрiзку M N за точку M необхiдно, по-перше, щоб γ не перетинала сам вiдрiзок, тобто, щоб виконувалася умова, протилежна до умови (1) :
(Ax1 + By1 + C ) (Ax2 + By2 + C ) > 0.
По-друге, необхiдно, щоб точка M знаходилася ближче до прямої γ, нiж
N |
γ Md1 d2O
точка N, тобто, щоб d1 вiдстань вiд точки M до прямої γ була менше, нiж d2 вiдстань вiд точки N до γ:
d |
|
= |
|Ax1 + Bx1 + C | |
< |
|Ax2 + Bx2 + C | |
= d |
, |
||||
|
1 |
|
√ |
|
|
|
√ |
|
|
2 |
|
|
|
A2 + B2 |
|
A2 + B2 |
|
||||||
спростивши цю нерiвнiсть, отримаємо другу умову:
|Ax1 + Bx1 + C | < |Ax2 + Bx2 + C | .
Таким чином, пряма γ перетинає продовження вiдрiзку M N за точку
M, якщо |
( |
Ax1 |
+ Bx1 |
+ C < Ax2 + Bx2 |
+ C . |
||
|
|||||||
|
(Ax1 |
+ By1 |
+ C) (Ax2 |
+ By2 |
+ C) > 0, |
||
|
| |
|
|
| | |
|
|
| |
Приклад 7.3. Скласти рiвняння бiсектрис кутiв, утворених двома перетинними прямими γ1 : 6x + y − 3 = 0 i γ2 : 2x + 12y + 9 = 0. Розв’язання. Скористаємося фактом, що бiсектриси кутiв, утворених двома перетинними прямими γ1 i γ2, це геометричне мiсце точок, рiвновiддалених вiд цих прямих. Iншими словами, деяка точка M (x, y) належить однiй з бiсектрис тодi i тiльки тодi, коли d1 вiдстань вiд точки M до прямої γ1 дорiвнює d2 вiдстанi вiд точки M до γ2 :
84

M |
γ |
|
1 |
γ2
d |
|
= |
|6x + y − 3| |
= |
|2x + 12y + 9| |
= d |
. |
|||||
|
|
|
|
|
|
|
||||||
|
1 |
|
√ |
|
|
|
2 |
√ |
2 |
|
||
|
|
|
37 |
|
|
37 |
|
|
|
|||
Ця рiвнiсть еквiвалентна такiй сукупностi:
"
12x + 2y − 6 = 2x + 12y + 9, 12x + 2y − 6 = −2x − 12y − 9.
Спростивши кожне з рiвнянь, отримаємо рiвняння двох бiсектрис кутiв, утворених прямими γ1 i γ2 :
"
2x − 2y − 3 = 0, 14x + 14y + 3 = 0.
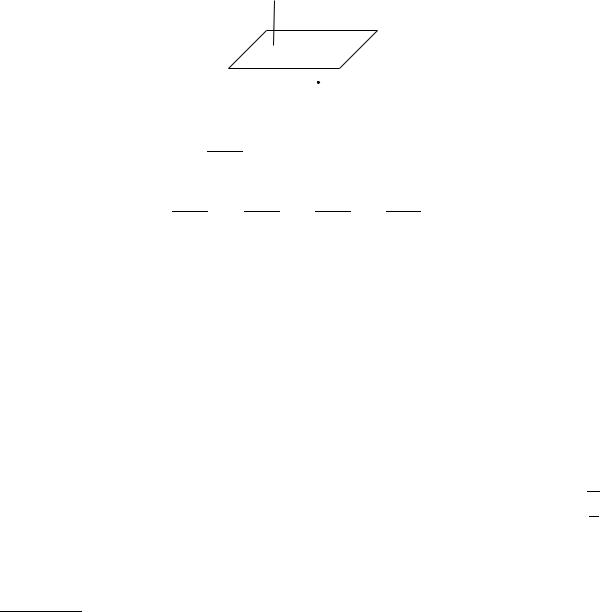
Приклад 7.4. Знайти вiдхилення δ i вiдстань d вiд точки M (2, −1, 4) до площини α : 2x − 3y + z − 4 = 0. В однiй чи в рiзних пiвпросторах вiдносно α лежать початок координат i точка M ?
Розв’язання. Запишемо нормальне рiвняння площини α. Нагадаємо, для того, щоб звести загальне рiвняння площини Ax + By + Cz + D = 0 до нормального, необхiдно це рiвняння домножити справа i злiва на
нормуючий множник µ = |
|
|
− sign D |
|
|
(тут вважаємо, що sign 0 = 1): |
|||||
|
√A2 + B2 + C2 |
|
|
|
|||||||
µAx + µBy + µCz + D = 0 |
|||||||||||
або |
|
|
Ax + By + Cz + D |
|
|||||||
|
|
|
|
||||||||
− sign D |
√ |
|
|
|
|
|
|
|
= 0 |
||
2 |
+ B |
2 |
+ C |
2 |
|
||||||
|
|
|
|
A |
|
|
|
|
|||
85
M
|
|
|
|
|
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
O |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||||
В нашiй ситуацiї µ = |
√ |
|
, нормальне рiвняння |
|
|||||||||||
14 |
|
||||||||||||||
α : |
2 |
x − |
3 |
y + |
1 |
z − |
4 |
|
= 0. |
||||||
√ |
|
√ |
|
√ |
|
√ |
|
||||||||
14 |
|
|
14 |
|
14 |
14 |
|
|
|||||||
Для того, щоб знайти δ вiдхилення вiд точки M до площини α, необхiдно в нормальне рiвняння площини замiсть змiнних x, y, z пiдставити координати точки M :
δ = √14 |
· 2 − √14 |
· (−1) + √14 |
· 4 − √14 |
= r |
|
|
. |
||||
2 |
|
||||||||||
2 |
3 |
1 |
4 |
7 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
Нагадаємо, що вiдхилення вiд точки до площини це вiдстань вiд точки до площини, взята iз знаком ”+”, якщо дана точка i початок координат лежать в рiзних пiвпросторах вiдносно заданої площини, iз знаком ”–”, якщо в однiй. r
Таким чином, вiдстань вiд точки M до α дорiвнює d = | δ | = 72.
Точка M i початок координат лежать в рiзних пiвпросторах вiдносно α, оскiльки δ > 0.
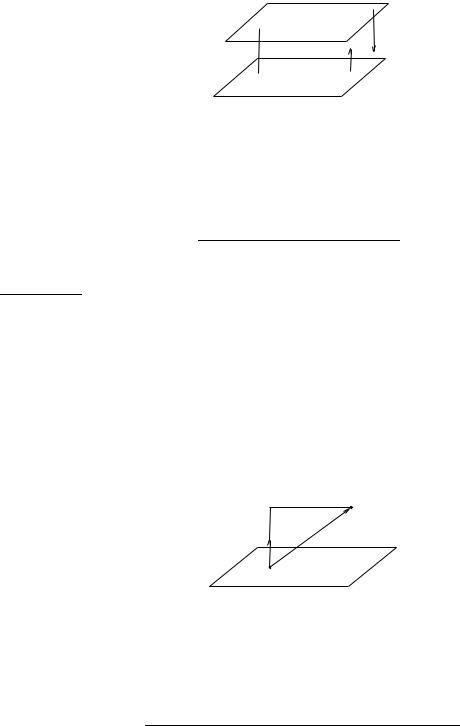
Приклад 7.5. Довести, що площини
α1 : x − 2y − 2z − 8 = 0 i α2 : −2x + 4y + 4z + 1 = 0
паралельнi i знайти вiдстань мiж ними.
Розв’язання. Площини α1 i α2 паралельнi, оскiльки їх вектори нормалi колiнеарнi. Дiйсно, ~n1 = {1, −2, 2} (вектор нормалi до α1) колiнеарен вектору ~n2 = {−2, 4, 4} (вектор нормалi до α2): −2~n1 = ~n2.
86
|
n2 |
d |
n1 |
 M
M
Знайдемо d вiдстань мiж площинами α1 i α2. Для цього вiзьмемо довiльну точку, яка належить площинi α1, наприклад, M (8, 0, 0) , тодi d
дорiвнює вiдстанi вiд точки M до площини α2 : |
|
|
||||
d = |
|−2 · 8 + 4 · 0 + 4 · 0 + 1| |
= |
5 |
. |
||
|
|
|
2 |
|||
|
√36 |
|
||||
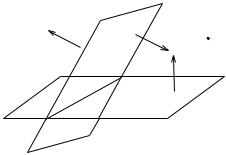
Приклад 7.6. Задано площину α : Ax + By + Cz + D = 0, позначимо через D+ = {(x, y) : Ax + By + Cz + D > 0} один з пiвпросторiв, на який площина α дiлить весь простiр. Довести, що вектор ~n = {A, B, C} спрямований в бiк пiвпростору D+.
Розв’язання. Нехай M0 (x0, y0, z0) довiльна точка площини α, тобто
Ax0 + By0 + Cz0 + D = 0.
Вiзьмемо довiльну точку M1 (x1, y1, z1) , яка належить пiвпростору
D+ : Ax1 + By1 + Cz1 + D > 0. Ми доведемо, що вектор ~n спрямований |
|||||
в бiк пiвпростору D |
+ |
, якщо покажемо, що Πp |
−−−→ |
0 |
|
|
|
|
~n |
M M > . |
|
|
|
|
0 1 |
|
|
|
|
|
M1 |
|
|
|
|
n |
D+ |
|
|
M0 |
α |
Дiйсно, |
|
|
|
|
|
−−−→0 1 ) |
||||
|
|
|
Πp |
−−−→ |
= |
( ~n, |
||||
|
|
|
|
= |
|
|||||
|
|
|
|
M M |
|
|
M M |
|||
|
|
|
~n |
|
|
|
|
|
||
|
|
|
0 1 |
|
|
|~n | |
||||
|
|
|
|
|
|
|
||||
|
|
= |
A (x1 − x0) + B (y1 − y0) + C (z1 − z0) |
= |
||||||
|
1 |
|
|
|
|~n | |
|
|
|
||
= |
(Ax1 + By1 + Cz1 + D − (Ax0 + By0 + Cz0 + D)) = |
|||||||||
|
||||||||||
|~n | |
||||||||||
87

1
= |~n | (Ax1 + By1 + Cz1 + D) > 0.
Приклад 7.7. Задано двi перетиннi площини αi : Aix+Biy+Ciz+Di = 0, i = 1, 2, i точкa M0 (x0, y0, z0) , яка не належить жоднiй з цих площин. Знайти необхiдну i достатню умову того, що M0 лежить всерединi гострого двогранного кута, утвореного при перетинi площин α1 i α2.
Розв’язання. Кожна площина розбиває простiр на два пiдпростори, позначимо їх
|
|
|
|
|
Di+ = {Aix + Biy + Ciz + Di > 0} , |
|
|
|
|||||
|
|
|
|
|
Di− = {Aix + Biy + Ciz + Di < 0} , |
|
D1+ |
T |
|||||
|
|
|
|
|
|
|
|
|
|
||||
де |
i = |
1, 2. Можливi |
чотири |
ситуацiї: |
a) M0 |
|
D2+, |
||||||
б) |
M0 |
|
D1+ |
D2−, в) M0 D1− |
D2+ або |
г) M0 |
|
D1− D2−. В |
|||||
кожнiй з цих |
ситуацiй запишемо умову того, що двогранний кут, в якому |
||||||||||||
|
T |
|
|
T |
|
|
|
T |
|
||||
знаходиться точка M0 є гострим. |
|
|
|
|
|
|
|
||||||
|
Розглянемо випадок a). Нехай M0 D1+ T D2+, тобто |
|
|
|
|||||||||
|
|
|
|
|
( A2x0 |
+ B2y0 |
+ C2z0 |
+ D2 |
> 0. |
|
|
|
|
|
|
|
|
|
A1x0 |
+ B1y0 |
+ C1z0 |
+ D1 |
> 0, |
|
|
|
|
Нагадаємо (див. задачу 7.6), що ~n1 = {A1, B1, C1} i ~n2 = {A2, B2, C2}
(вектори нормалi до площин α1 i α2, вiдповiдно) направленi в бiк дво- |
|||
гранного кута D1+ T D2+. Отже, двогранний+ кут D1+ T D2+ буде гострим, |
|||
α2 |
D2 |
M |
|
n2 |
|||
|
0 |
||
|
n1 |
D+ |
|
|
|
1 |
|
|
α1 |
|
|
якщо кут мiж векторами ~n1 i ~n2 буде тупим, тобто скалярний добуток
88
цих векторiв буде вiд’ємним: ( ~n1, ~n2 ) = A1A2 + B1B2 + C1C2 < 0. Таким чином, у випадку а) буде така вiдповiдь:
|
A2x0 |
+ B2y0 |
+ C2z0 |
+ D2 |
> 0, |
|||||||||
|
|
A1x0 |
+ B1y0 |
+ C1z0 |
+ D1 |
> 0, |
||||||||
|
A1A2 + B1B2 + C1C2 < 0. |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
зводяться до розглянутого |
вище. Покажемо, як це |
||||||||||||
Всi iншi випадки |
|
|
|
|
|
|
|
|
|
|
|
|
||
зробити, на прикладi випадку б). Нехай M0 D1+ T D2−, тобто |
||||||||||||||
|
( A2x0 |
+ B2y0 |
+ C2z0 |
+ D2 |
< 0 |
|||||||||
|
|
A1x0 |
+ B1y0 |
+ C1z0 |
+ D1 |
> 0, |
||||||||
або |
( |
|
A2x0 |
|
B2y0 |
|
C2z0 |
|
D2 |
> 0. |
||||
|
A1x0 + B1y0 + C1z0 + D1 > 0, |
|||||||||||||
|
− |
|
|
− |
|
|
− |
|
|
− |
|
|
|
|
Тодi, розглянувши замiсть вектора ~n2 = {A2, B2, C2} , вектор −~n2 = {−A2, −B2, −C2} отримаємо умову того, що кут мiж векторами ~n1 i −~n2 є тупим:
( ~n1, −~n2 ) = −A1A2 − B1B2 − C1C2 < 0
або
A1A2 + B1B2 + C1C2 > 0.
Це i буде означати, що двогранний кут D1+ |
T |
D2− буде гострим. |
|
|
|||
|
|
- |
|
D2+ α2 |
D2 |
M |
|
n |
-n |
|
0 |
2 |
|
||
2 |
|
n1 |
D+ |
|
|
||
|
|
|
1 |
|
α1 |
|
|
89

Таким чином, у випадку б) буде така вiдповiдь:
|
A2x0 |
+ B2y0 |
+ C2z0 |
+ D2 |
< 0, |
|||||||
|
|
A1x0 |
+ B1y0 |
+ C1z0 |
+ D1 |
> 0, |
||||||
|
A1A2 + B1B2 + C1C2 > 0. |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Скориставшись |
схожими мiркуваннями, запишемо вiдповiдi у випадках |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
||
в) i г) : |
в) |
A2x0 |
+ B2y0 |
+ C2z0 |
+ D2 |
> 0, |
||||||
|
||||||||||||
|
|
|
A1x0 |
+ B1y0 |
+ C1z0 |
+ D1 |
< 0, |
|||||
|
|
A1A2 + B1B2 + C1C2 > 0. |
||||||||||
|
|
A1x0 + B1y0 + C1z0 + D1 < 0, |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
г) |
A2x0 + B2y0 + C2z0 + D2 < 0, |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
A1A2 + B1B2 + C1C2 < 0.
Всi чотири отриманi вiдповiдi можна об’єднати в одну:
(A1A2 + B1B2 + C1C2) (A1x0 + B1y0 + C1z0 + D1) ×
× (A2x0 + B2y0 + C2z0 + D2) < 0.
Задачi для самостiйної роботи
Нормальне рiвняння прямої на площинi
7.1. Знайти вiдхилення δ i вiдстань d вiд точки M до прямої γ. В однiй чи в рiзних пiвплощинах вiдносно γ лежать початок координат i точка
M ?
а) M (1, 2), γ : x − 7 = 0;
б) M (2, −15), γ : y + 9 = 0;
в) M (3, 4), γ : 4x − 3y − 15 = 0;
г) M (9, 1), γ : −2x + 6y + 7 = 0;
90
