
- •1. Основні аспекти математичного моделювання економіки.
- •2. Задача лінійного програмування. Постановка. Геометрична інтерпретація (загальна). Методи розв’язання.
- •3. Геометрична інтерпретація задачі лінійного програмування (детальна).
- •4. Симплекс-метод. Сутність методу. Основні поняття. Алгоритм.
- •5) Аналіз моделей на чутливість.
- •6) Двоїстість у лінійному програмуванні. Структура та властивості двоїстих задач.
- •7) Перша теорема двоїстості. Її економічний зміст.
- •8) Друга теорема двоїстості. Її економічний зміст.
- •9) Економічний зміст змінних та обмежень двоїстих задач. Зв’язок між змінними двоїстих моделей.
- •10) Третя теорема двоїстості. Її економічний зміст. Поняття цінності ресурсу, та його використання в економічному аналізі задач.
- •11) Транспортна модель.
- •12) Лінійні цілочисельні задачі.
- •13) Задачі нелінійного програмування.
- •14) Поняття економетричного моделювання. Зв’язок економетрії з іншими науками. Етапи економетричного моделювання.
- •15) Парна регресія. Оцінка лінійної залежності двох змінних.
- •16) Класична лінійна модель множинної регресії.
- •17) Оцінка якості регресійної моделі та статистична значущість коефіцієнтів регресії. Оценка качества регрессионной модели характеризуется рядом показателей:
- •1) Постановка задачі лінійного програмування
- •15) Визначення опорного плану транспортної задачі
- •23) Поняття коефіцієнта коваріації
- •24) Поняття коефіцієнта кореляції
- •25) Поняття коефіцієнта детермінації
- •26) Визначення рівняння регресії
15) Парна регресія. Оцінка лінійної залежності двох змінних.
Постановка задачи: пусть имеется N-пар выборочных наблюдений за двумя переменными X и Y. Требуется на основе этих выборочных наблюдений статистически объяснить зависимость Y от X и проверить оптимальность полученной оценки. Зависимость Y от X будем искать в виде: Y=f(x)+u, где f(x) – ф-ия регрессии, u – случайная остаточная компонента.
Присутствие в модели «u» обусловлено следующими причинами: 1) ошибка спецификации: можно ошибочно не включить важные объясняющие переменные в модель, или исп-ть агрегированные (обобщённые) переменные; 2) ошибка измерения: связана со сложностью сбора исходных данных и исп-ия в модели латентных (неявных) переменных, кот-е нельзя измерить непосредственно; 3) ошибка, связанная с человеческим фактором: участие Ч. в сборе и подготовке данных вносит эл-ты непредсказуемости.
Относительно
компоненты «u» в модель регрессии
вносится ряд гипотез, известных как
усл-ия Гаусса-Маркова: 1) Мат.ожидание
ui = 0.
![]() =
0. Это требование означает, что не должно
быть систематического смещения ошибки
ни в сторону положительных, ни в сторону
отриц.значений. Среднее значение
случ.остатка должно быть=0.
=
0. Это требование означает, что не должно
быть систематического смещения ошибки
ни в сторону положительных, ни в сторону
отриц.значений. Среднее значение
случ.остатка должно быть=0.
2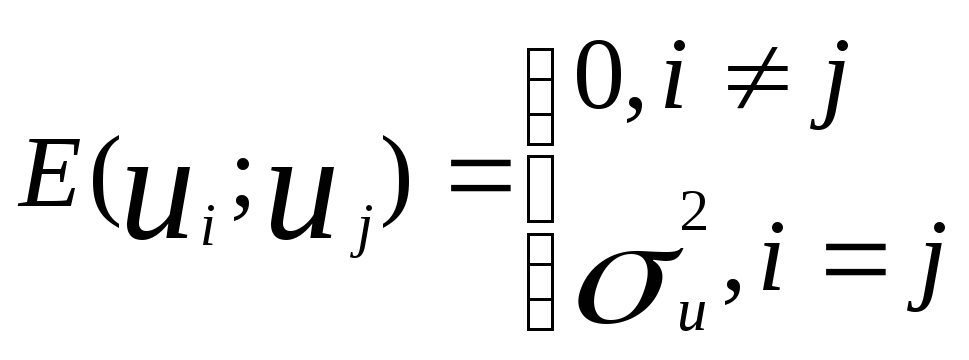 .
1-ая строчка предполагает, что остатки,
полученные в разл.наблюдениях независимы
друг от друга. 2-ая строчка означает
постоянство дисперсии остатков,
т.е.независимость от того, при каких
значениях производятся наблюдения.
.
1-ая строчка предполагает, что остатки,
полученные в разл.наблюдениях независимы
друг от друга. 2-ая строчка означает
постоянство дисперсии остатков,
т.е.независимость от того, при каких
значениях производятся наблюдения.
3) Переменные Х (наблюдаемые значения) явл. неслучайными вел-и. Т.о. задача регрессии имеет вид:
Y=f(x)+u
![]() =
0
=
0
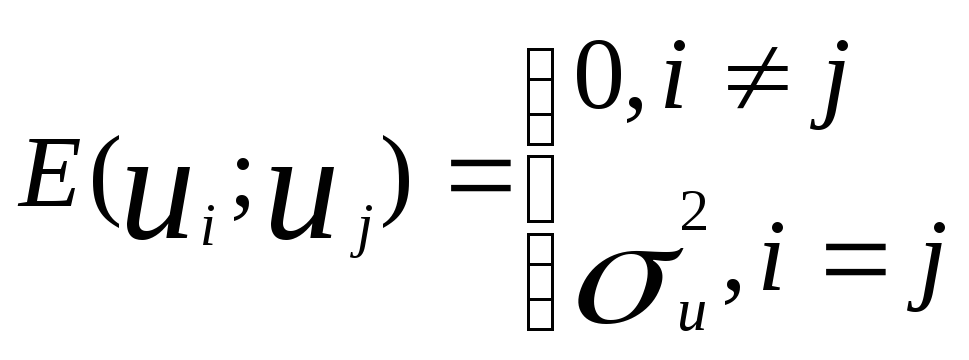
Х1…ХN – неслуч.вел-ы.
Ф-ия f(x) может быть как лин-ой так и нелин-ой. При выборе её вида обычно пользуются следующ.рекомендациями: 1) исп-тся априорная инф-ция о содержательной эк.сущности анализируемой зависимости; 2) предварительный анализ зависимости с помощью визуализации (графический способ); 3) Исп-ие различных статистических приёмов обработки данных.
Важная
проблема регрессионного анализа:
определить на сколько хороши полученные
оценки параметров и уравнение в целом.
Для объяснения лин.связи между переменными
можно исп-ть коэф-т ковариации. Рассмотрим
поле наблюдений:
![]() (график).
(график).
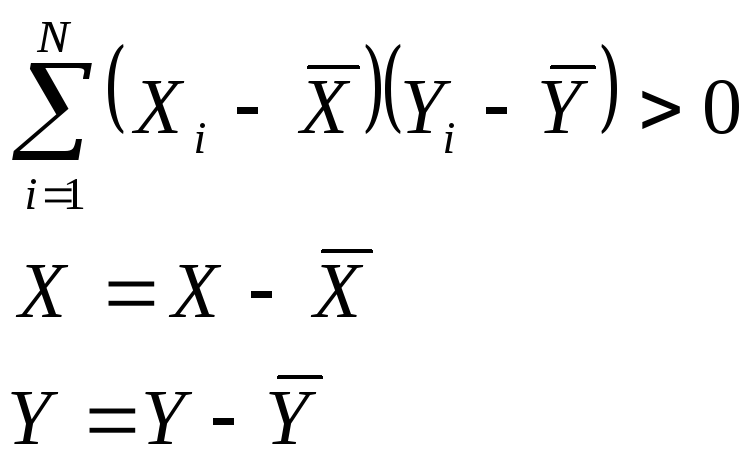
Разобьем
наблюдение на 4 квадрата, разместив
начало координат в т.![]() ,
тогда все исходные наблюдения будут
пересчитаны по правилу:
,
тогда все исходные наблюдения будут
пересчитаны по правилу:
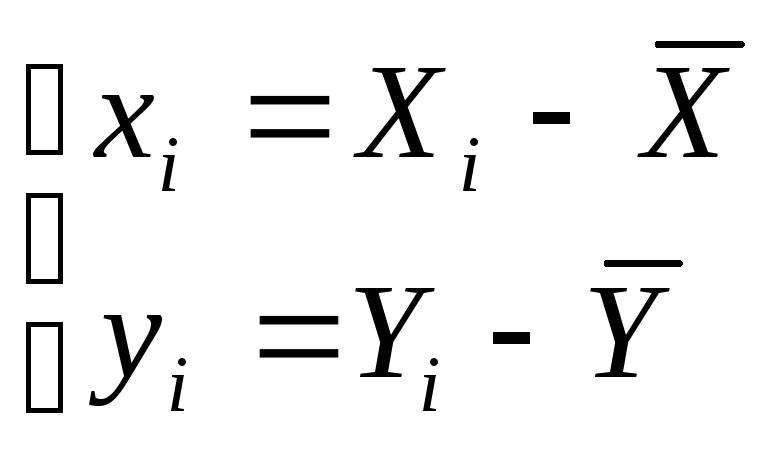
Тогда
понятно, что для точек 1-ой и 3-ей четверти
![]() .
Для точек 2-ой и 4-ой четверти
.
Для точек 2-ой и 4-ой четверти![]() .
Т.о. вел-а
.
Т.о. вел-а![]() может служить мерой лин.зависимости
между переменными. Если большая часть
точек лежит в 1-ой и 3-ей четверти, то
может служить мерой лин.зависимости
между переменными. Если большая часть
точек лежит в 1-ой и 3-ей четверти, то![]() => имеется лин.полож.зависимость. Если
большая часть точек лежит в 2-ой и 4-ой
четверти, то
=> имеется лин.полож.зависимость. Если
большая часть точек лежит в 2-ой и 4-ой
четверти, то![]() .
=> имеется лин.отриц.зависимость. Если
точки рассеиваются по всем четвертям,
то
.
=> имеется лин.отриц.зависимость. Если
точки рассеиваются по всем четвертям,
то![]() близка к нулю => лин.связи между
переменными нет. (графики). Рассмотренная
мера называется ковариацией и зависит
от ед-ц измерения Х и Y, поэтому она может
принимать разл.значения для одних и тех
же наблюдений, если они измерены в разных
масштабах (это является недостатком
коэффициента ковариации).
близка к нулю => лин.связи между
переменными нет. (графики). Рассмотренная
мера называется ковариацией и зависит
от ед-ц измерения Х и Y, поэтому она может
принимать разл.значения для одних и тех
же наблюдений, если они измерены в разных
масштабах (это является недостатком
коэффициента ковариации).
Если
избавить исходные наблюдения от ед-ц
измерения и перейти к стандартизированным
данным, например по формуле
![]() ,
то коэф-т ковариации будет вычисляться
по такой формуле:
,
то коэф-т ковариации будет вычисляться
по такой формуле: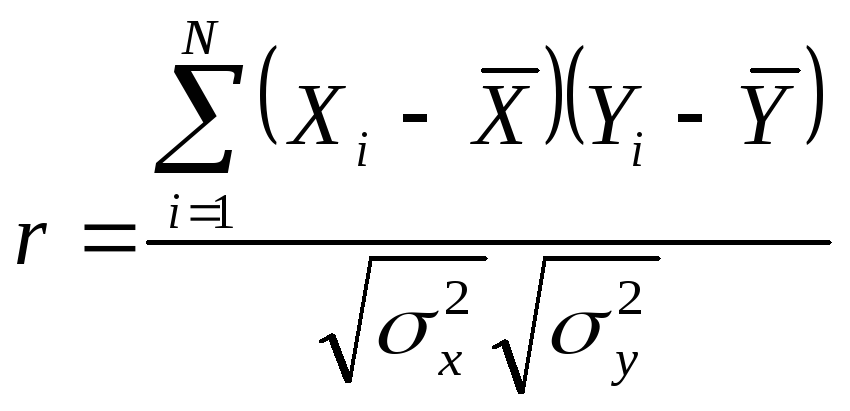 ,
и будет назывться коэф-м корреляции.
,
и будет назывться коэф-м корреляции.![]() .
Если r=1, имеем сильную лин.полож.связь.
Если r=-1 - сильную лин.отриц.связь. r=0,
лин.зависимость между переменными не
наблюдается.
.
Если r=1, имеем сильную лин.полож.связь.
Если r=-1 - сильную лин.отриц.связь. r=0,
лин.зависимость между переменными не
наблюдается.
Коэф-т
корреляции обладает св-вом симметричности
![]() (вычисляется также и для многомерных
вел-н). Замечание: следует иметь ввиду,
что коэф-т корреляции ничего не говорит
о причинно-следственных связях между
переменными. (Х явл причиной Y, или
наоборот). Поэтому следует избегать
т.н. ложных корреляций, т.е. нельзя
пытаться связать явления, между кот-ми
отсутствуют реальные причинно-следственные
связи. Т.о. при построении регрессионной
модели при выборе факторов нужно исходить
из содержания задачи и анализа
«причина-следствие».
(вычисляется также и для многомерных
вел-н). Замечание: следует иметь ввиду,
что коэф-т корреляции ничего не говорит
о причинно-следственных связях между
переменными. (Х явл причиной Y, или
наоборот). Поэтому следует избегать
т.н. ложных корреляций, т.е. нельзя
пытаться связать явления, между кот-ми
отсутствуют реальные причинно-следственные
связи. Т.о. при построении регрессионной
модели при выборе факторов нужно исходить
из содержания задачи и анализа
«причина-следствие».
На
ряду с коэф-ом корреляции рассматривается
вел-а, кот-я равна
 .
Этот показатель наз-тся коэф-ом
детерминации и показывает долю дисперсии
Y, объяснённой лин.зависимостью от Х.
Чем лучше регрессия соответствует
наблюдениям, тем меньше
.
Этот показатель наз-тся коэф-ом
детерминации и показывает долю дисперсии
Y, объяснённой лин.зависимостью от Х.
Чем лучше регрессия соответствует
наблюдениям, тем меньше![]() и тем ближе
и тем ближе![]() к 1. И наоборот: чем хуже регрессия
подогнана к исходным данным, тем ближе
к 1. И наоборот: чем хуже регрессия
подогнана к исходным данным, тем ближе![]() к 0. Коэф-т детерминации
к 0. Коэф-т детерминации![]() используют как меру качества статистического
подбора модели.
используют как меру качества статистического
подбора модели.
