24) Поняття коефіцієнта кореляції

Коэффициент корреляции — это показатель взаимного вероятностного влияния двух случайных величин. Коэффициент корреляции R может принимать значения от -1 до +1. Если абсолютное значение находится ближе к 1, то это свидетельство сильной связи между величинами, а если ближе к 0 — то, это говорит о слабой связи или ее отсутствии. Если абсолютное значение R равно единице, то можно говорить о функциональной связи между величинами, то есть одну величину можно выразить через другую посредством математической функции. Вычислить коэффициент корреляции можно по формуле:

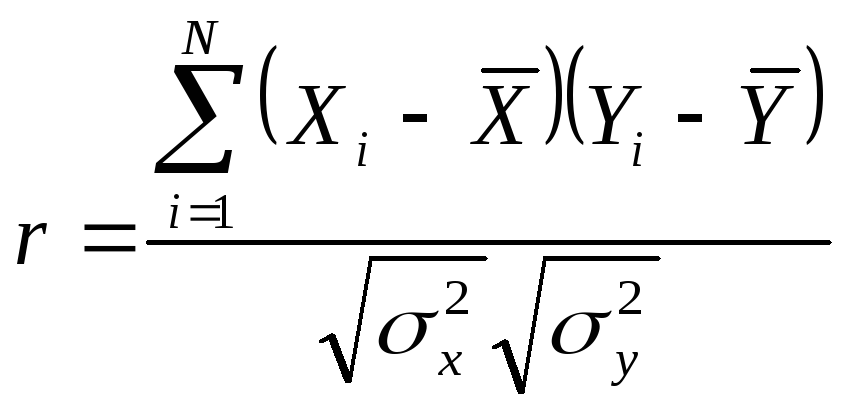
25) Поняття коефіцієнта детермінації

На ряду с коэф-ом корреляции рассматривается вел-а, кот-я равна 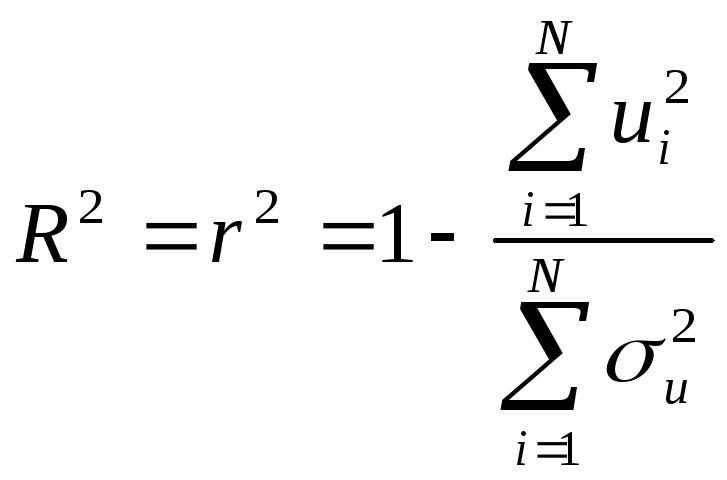. Этот показатель наз-тся коэф-ом детерминации и показывает долю дисперсии Y, объяснённой лин.зависимостью от Х. Чем лучше регрессия соответствует наблюдениям, тем меньшеи тем ближек 1. И наоборот: чем хуже регрессия подогнана к исходным данным, тем ближек 0. Коэф-т детерминациииспользуют как меру качества статистического подбора модели.

26) Визначення рівняння регресії

Уравнение регрессии представляет собой функциональную связь, при которой по любому значению х можно однозначно определить значение у. Функциональная связь лишь приближенно отражает связь реальную, причем степень этого приближения может быть различной и зависит она как от свойств исходных данных, так и от выбора вида функции, по которой производится выравнивание.