
- •Передмова
- •1. Перестановки та підстановки
- •1, 2, …, N.
- •2. Визначники
- •2.1. Матриці. Загальні відомості
- •2.2. Визначники другого та третього порядків
- •2.3. Визначники n-го порядку
- •2.4. Властивості визначників
- •2.5. Мінори та їх алгебраїчні доповнення
- •2.6. Розклад визначника за елементами рядка або стовпця
- •2.7. Знаходження визначника зведенням до трикутного виду
- •3. Алгебра матриць
- •3.1. Додавання матриць і множення матриці на число
2.7. Знаходження визначника зведенням до трикутного виду
Цей
метод полягає у перетворенні визначника
до такого вигляду, коли всі елементи,
які знаходяться по один бік від однієї
з діагоналей, дорівнюють нулю. У випадку,
коли це головна діагональ, визначник
дорівнює добутку елементів цієї
діагоналі. Якщо це бічна діагональ і
визначник має порядок n,
то він дорівнює добутку елементів
діагоналі, помноженому на число
![]() .
.
Приклад 2.14. Обчислимо визначник
 ,
,
звівши його до трикутного виду.
До другого рядка визначника додамо перший рядок, помножений на (–2), потім до третього рядка додамо перший, і до четвертого рядка додамо перший, помножений на (–3). Від цих перетворень значення визначника не зміниться. Отже, будемо мати:
 .
.
До третього рядка отриманого визначника додамо його другий рядок, помножений на 3, а до четвертого – другий, помножений на (–3). За результатом цих перетворень, які не змінять значення визначника, отримаємо
 .
.
Тепер до четвертого рядка, помноженого на 2, додамо третій рядок. Після такого перетворення визначник помножиться на 2, а, значить, будемо мати:
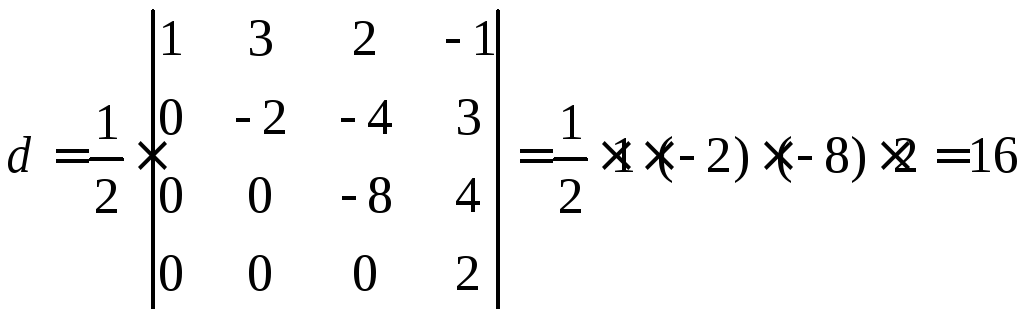 .
.
Приклад 2.15. Обчислимо визначник
 .
.
Від останнього стовпця визначника віднімемо всі попередні стовпці
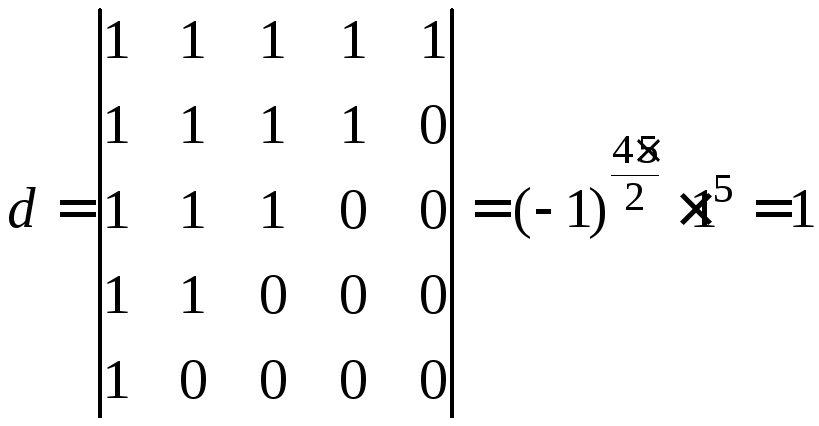 .
.
Приклад 2.16. Обчислимо визначник n-го порядку
 .
.
Перший рядок визначника додамо до всіх інших. У результаті цього перетворення ми отримаємо

Приклад 2.17. Обчислимо визначник

порядку n.
До першого стовпця визначника додамо суму всіх інших стовпців, а потім число (n – 1) винесемо із першого стовпця за знак визначника
 =
=
 .
.
Перший рядок перетвореного визначника віднімемо від усіх інших рядків
 .
.
Задача 2.25. Обчислити подані визначники зведенням до трикутного виду:
а)
 ;б)
;б)
 ;в)
;в)
 ;
;
г)
 ;д)
;д)
 ;е)
;е)
 ;
;
подані нижче визначники мають порядок n:
є)
 ;ж)
;ж)
 ;
;
з)
 ;і)
;і)
 .
.
Задача
2.26.
Обчислити визначник матриці
![]() ,
елементи якої задані умовами
,
елементи якої задані умовами![]() .
.
Задача
2.27.
Обчислити визначник матриці
![]() ,
елементи якої задані умовами
,
елементи якої задані умовами![]() .
.
3. Алгебра матриць
3.1. Додавання матриць і множення матриці на число
Розглянемо деякі природні операції над матрицями.
Сумою
A
+ B
двох
матриць
![]() і
і
![]() однакових розмірів k
n
називається матриця
однакових розмірів k
n
називається матриця
![]() того ж розміру, елементи якої визначаються
за правилом
того ж розміру, елементи якої визначаються
за правилом
![]() (
1
i
k,
1
j
n).
(
1
i
k,
1
j
n).
Інакше кажучи, щоб отримати суму двох матриць однакових розмірів, потрібно додати їх елементи, що стоять на тих самих місцях. Операція утворення суми матриць називається їх додаванням.
