
- •Передмова
- •1. Перестановки та підстановки
- •1, 2, …, N.
- •2. Визначники
- •2.1. Матриці. Загальні відомості
- •2.2. Визначники другого та третього порядків
- •2.3. Визначники n-го порядку
- •2.4. Властивості визначників
- •2.5. Мінори та їх алгебраїчні доповнення
- •2.6. Розклад визначника за елементами рядка або стовпця
- •2.7. Знаходження визначника зведенням до трикутного виду
- •3. Алгебра матриць
- •3.1. Додавання матриць і множення матриці на число
2.3. Визначники n-го порядку
Усякий член визначника другого порядку є добутком двох елементів, які знаходяться в різних рядках і різних стовпцях матриці. Всі добутки такого виду, які можна скласти із елементів матриці другого порядку, є доданками у виразі для визначника, причому один із добутків береться із знаком «+», а другий із знаком «–». Так само кожний доданок виразу визначника для матриці третього порядку, який береться із знаком «+» або «–» є добутком елементів, розміщених у різних рядках та різних стовпцях матриці третього порядку, причому знову всі такі добутки є доданками виразу для визначника, взятими із знаком «+» або «–».
Нехай
![]() – квадратна матриця порядку n
з елементами
– квадратна матриця порядку n
з елементами
![]() .
Кожній підстановці
.
Кожній підстановці
![]() n-го
степеня поставимо у відповідність
добуток
n-го
степеня поставимо у відповідність
добуток
![]() .
.
Множники
цього добутку розміщені в різних рядках
і різних стовпцях матриці A,
причому в добутку є елемент із кожного
рядка матриці та елемент із кожного її
стовпця. Перебираючи всі підстановки
n-го
степеня, ми отримаємо всі добутки такого
виду. Добутки
![]() називаютьсячленами
визначника матриці A.
називаютьсячленами
визначника матриці A.
Визначником
матриці
![]() називається алгебраїчна сума n!
членів, яка складається таким чином:
кожен член є добутком n
елементів,
узятих по одному з кожного рядка і по
одному з кожного стовпця матриці A,
причому добуток
називається алгебраїчна сума n!
членів, яка складається таким чином:
кожен член є добутком n
елементів,
узятих по одному з кожного рядка і по
одному з кожного стовпця матриці A,
причому добуток
![]() береться із знаком «+», якщо підстановка
береться із знаком «+», якщо підстановка![]() парна та із знаком «–», якщо
парна та із знаком «–», якщо![]() – непарна.
– непарна.
Елементи матриці A, її діагоналі, рядки та стовпці ми будемо називати відповідно елементами, діагоналями, рядками та стовпцями визначника матриці A.
Приклад 2.2. Користуючись означенням визначника в загальному вигляді, знайдемо визначники матриць другого і третього порядків. Нехай
 .
.
У множині підстановок другого степеня два елементи:
 і
і
 .
.
Оскільки
підстановка
![]() парна, а
парна, а![]() – непарна, то маємо:
– непарна, то маємо:
![]() .
.
Розглянемо тепер матрицю

третього порядку.
Випишемо всі шість підстановок степеня 3:
 ,
,
 ,
, ,
,
 ,
,
 і
і .
.
Підстановки
![]() є парними, а
є парними, а![]() – непарними. Звідси виходить такий
вираз для визначника матриціA:
– непарними. Звідси виходить такий
вираз для визначника матриціA:
detA
=
![]() +
+
![]() +
+
![]() –
–
–
![]() –
–![]() –
–![]() =
=
=
![]() .
.
Для визначників другого та третього порядку ми отримали такі самі вирази, як і вище.
Приклад 2.3. З’ясуємо, які з добутків
![]() ,
,
![]() ,
,
![]() ,
,
![]()
входять
до розкладу визначника матриці
![]() і з якими знаками.
і з якими знаками.
Розглянемо
добуток
![]() .
A
– матриця п’ятого порядку, а, значить,
кожен із членів визначника A
є добутком п’яти елементів матриці A.
Оскільки
.
A
– матриця п’ятого порядку, а, значить,
кожен із членів визначника A
є добутком п’яти елементів матриці A.
Оскільки
![]() є добутком чотирьох елементів, то він
не входить до розкладу визначника A.
є добутком чотирьох елементів, то він
не входить до розкладу визначника A.
У
добутку
![]() п’ять
множників, які взяті по одному із кожного
рядка та із кожного стовпця матриці
A,
отже, цей добуток є членом визначника
A.
Визначимо
знак, з яким він входить до розкладу
визначника.
Оскільки
підстановка
п’ять
множників, які взяті по одному із кожного
рядка та із кожного стовпця матриці
A,
отже, цей добуток є членом визначника
A.
Визначимо
знак, з яким він входить до розкладу
визначника.
Оскільки
підстановка
 непарна, то член
непарна, то член
![]() входить до розкладу визначника матриці
A
із знаком «–».
входить до розкладу визначника матриці
A
із знаком «–».
Розмірковуючи
аналогічно, отримаємо, що
![]() також є членом визначника матриці A.
Підстановка
також є членом визначника матриці A.
Підстановка
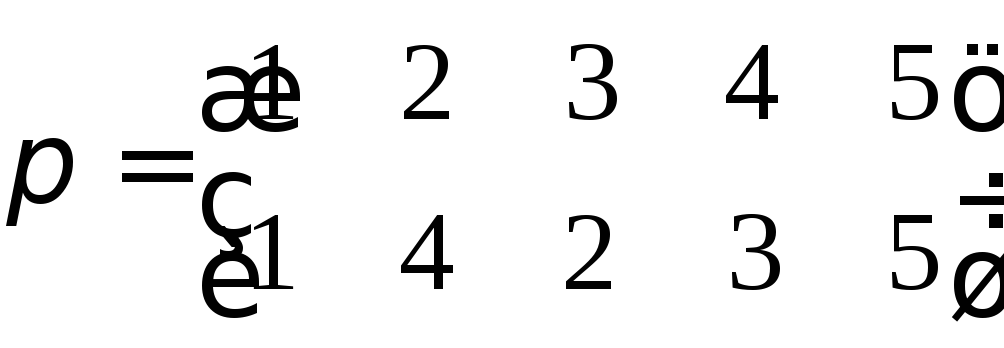 є парною, а, значить, член
є парною, а, значить, член
![]() входить до розкладу визначника A
із знаком «+».
входить до розкладу визначника A
із знаком «+».
Добуток
![]() не є членом визначника матриці A,
оскільки він містить два елементи із
третього стовпця:
не є членом визначника матриці A,
оскільки він містить два елементи із
третього стовпця:
![]() і
і
![]() .
.
Приклад
2.4.
Нехай
![]() .
Покажемо, що добуток елементів головної
діагоналі та добуток елементів бічної
діагоналі є членами визначника матриці
A
і з’ясуємо, з якими знаками вони входять
до розкладу визначника A.
.
Покажемо, що добуток елементів головної
діагоналі та добуток елементів бічної
діагоналі є членами визначника матриці
A
і з’ясуємо, з якими знаками вони входять
до розкладу визначника A.
Добутки
![]() і
і
![]() елементів головної та бічної діагоналей
відповідно складаються із n
множників, узятих по одному з кожного
рядка та з кожного стовпця матриці A,
а, значить, є членами визначника A.
Визначимо знак, з яким добуток елементів
головної діагоналі входить до визначника.
Оскільки підстановка
елементів головної та бічної діагоналей
відповідно складаються із n
множників, узятих по одному з кожного
рядка та з кожного стовпця матриці A,
а, значить, є членами визначника A.
Визначимо знак, з яким добуток елементів
головної діагоналі входить до визначника.
Оскільки підстановка
 є парною, то добуток елементів головної
діагоналі входить до розкладу визначника
матриціA
із знаком «+».
є парною, то добуток елементів головної
діагоналі входить до розкладу визначника
матриціA
із знаком «+».
У
прикладі 1.6. було показано, що підстановка
 є парною, якщо число
є парною, якщо число![]() парне, і непарною
у протилежному випадку.
парне, і непарною
у протилежному випадку.
Отже,
добуток елементів бічної діагоналі
входить до розкладу визначника матриці
![]() із знаком
із знаком
![]() .
.
Приклад 2.5. Обчислимо визначник
 .
.
Поданий
визначник є визначником матриці п’ятого
порядку, а, значить, кожен член визначника
є добутком п’яти
елементів. У матриці лише п’ять
відмінних від нуля елементів і вони
розташовані по одному в кожному рядку
матриці і по одному в кожному стовпці.
Отже,
серед членів визначника тільки один
ненульовий – це добуток
![]() .
Підстановка
.
Підстановка
 є непарною, отже, добуток
є непарною, отже, добуток
![]() входить до розкладу визначника із знаком
«–», а, значить, визначник дорівнює
числу –120.
входить до розкладу визначника із знаком
«–», а, значить, визначник дорівнює
числу –120.
Задача
2.2.
Які з поданих добутків входять до
розкладу визначника матриці
![]() і з якими знаками?
і з якими знаками?
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
;
г)
![]() ;
д)
;
д)
![]() ;
е)
;
е)
![]() ;
;
є)
![]() .
.
Задача 2.3. З яким знаком входить добуток
![]()
до
розкладу визначника матриці
![]() ?
?
Задача 2.4. Вибрати значення i та j так, щоб добуток
![]()
входив
до розкладу визначника матриці
![]() із знаком «+».
із знаком «+».
Задача 2.5. Вибрати значення i, j, k так, щоб добуток
![]()
входив
до розкладу визначника матриці
![]() із знаком «–».
із знаком «–».
Задача 2.6. У матриці A порядку n кількість відмінних від нуля елементів дорівнює числу n – 1. Чому дорівнює detA?
Задача 2.7. У матриці A порядку n у точності n елементів дорівнюють 1, а всі інші елементи – нулі. Чому може дорівнювати detA?
Задача 2.8. Обчислити подані визначники:
а)
 ;б)
;б)
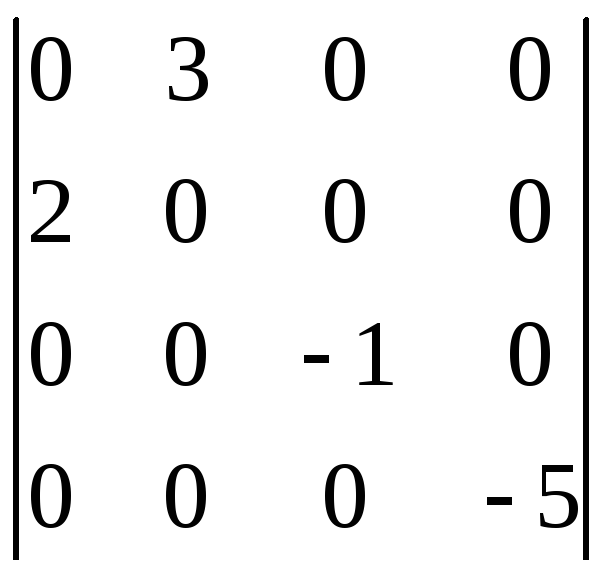 ;в)
;в)
 ;г)
;г)
 ;
;
д)
 ;е)
;е)
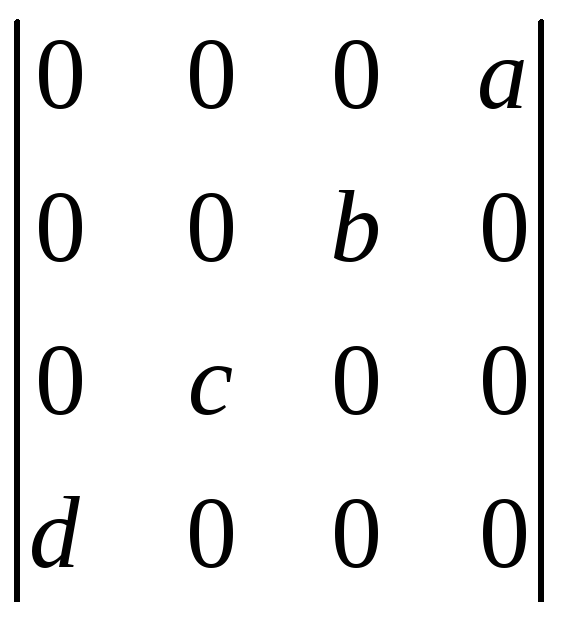 ;є)
;є)
 ;ж)
;ж)
 .
.
Задача 2.9. Обчислити визначник матриці A порядку n.
а) A = E; б) A = –E; в) A = diag(1, 2, …, n); г) A – матриця, всі елементи деякого рядка якої дорівнюють нулю; д) A – матриця, всі елементи деякого стовпця якої дорівнюють нулю;
е)
 ;
є)
;
є)
 ;
;
ж)
 ;
з)
;
з)
 .
.
Задача
2.10.
Обчислити визначник матриці
![]() ,
в якій
,
в якій
![]() ,
,
а всі інші елементи дорівнюють нулю.
