
zadmeh2
.docЗадача 3.1. Задано матриці:
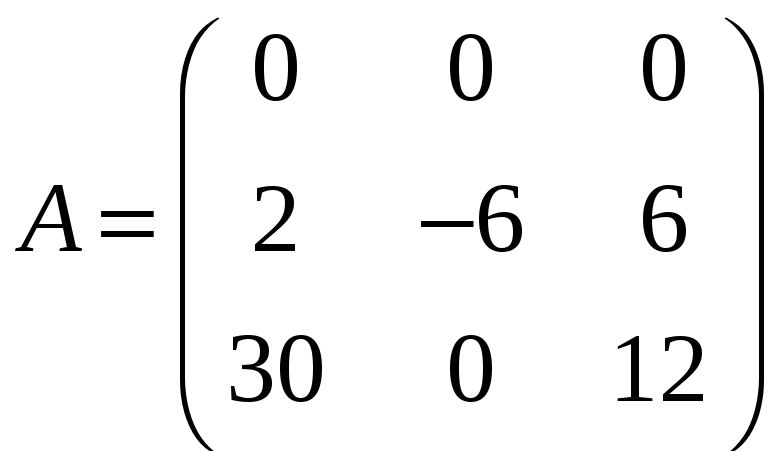 ,
,
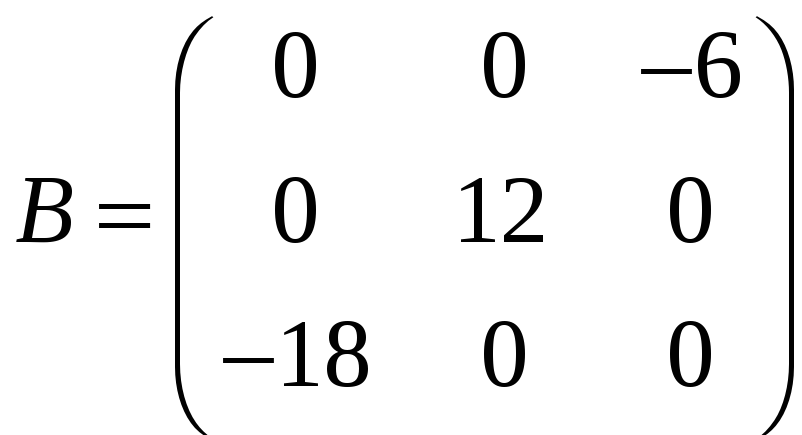 ,
,
 .
.
Знайти:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
.
Задача 3.2. Знайти матрицю X, якщо:
а)
 ;
б)
;
б)
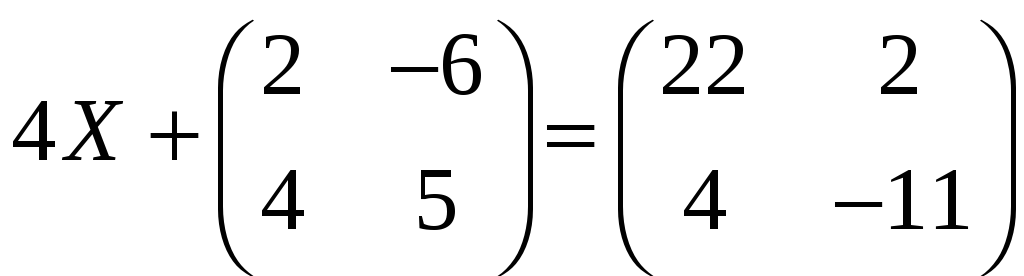 ;
в)
;
в)
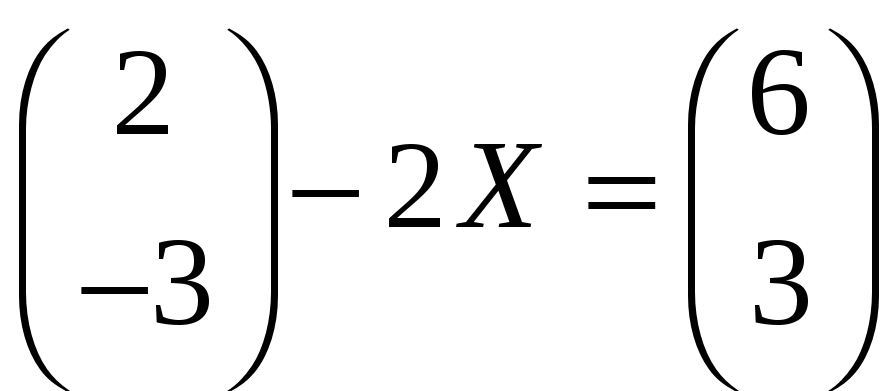 ;
;
г)
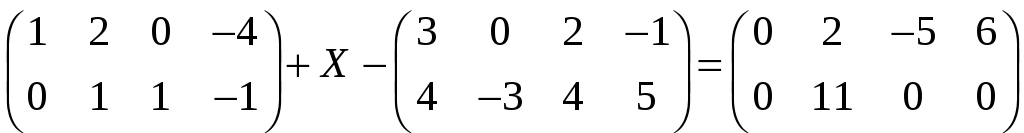 ;
;
д)
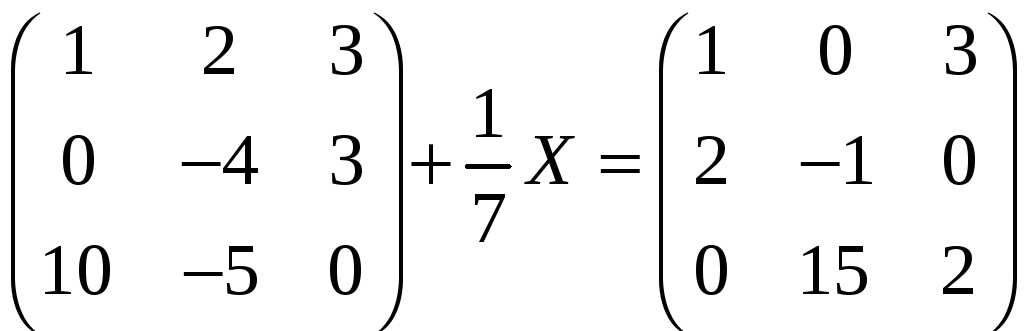 .
.
Задача 3.3. Знайти матриці X та Y, якщо:
а)
 б)
б)
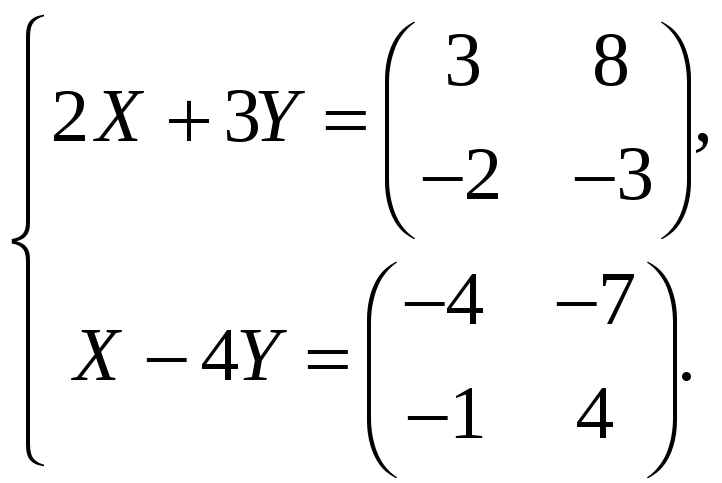
Задача 3.4. Знайти добутки AB і BA, якщо:
а)
 ,
,
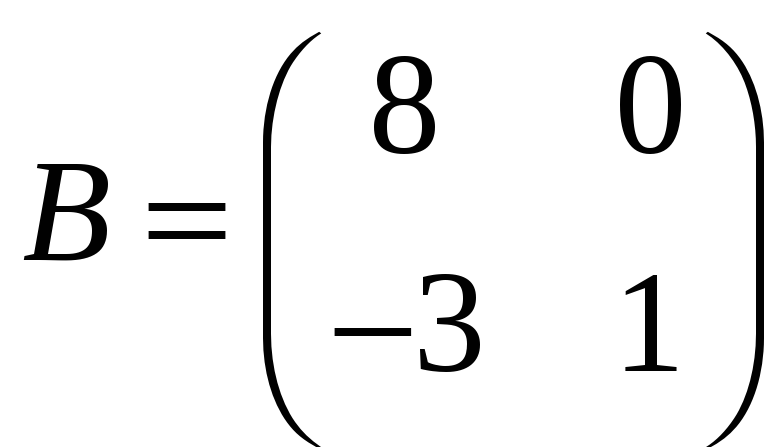 ;
б)
;
б)
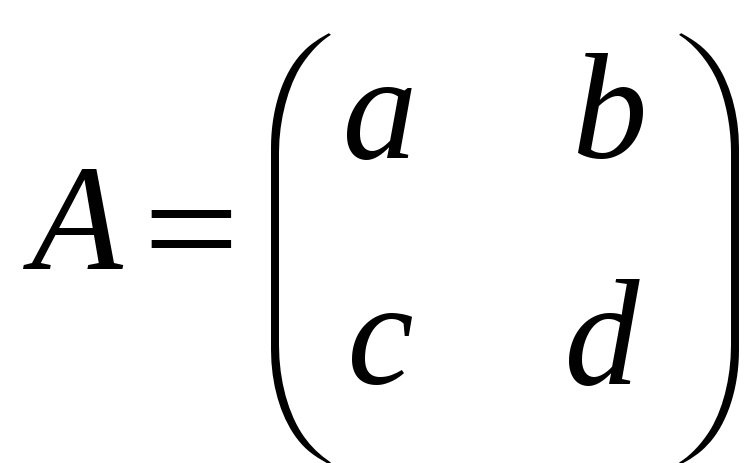 ,
,
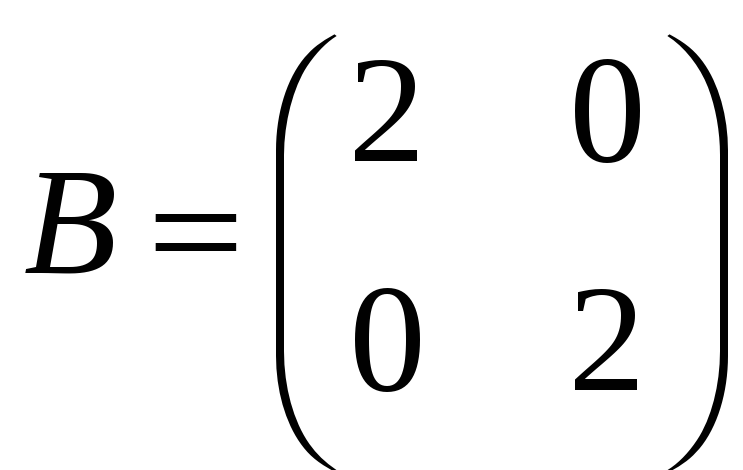 ;
;
в)
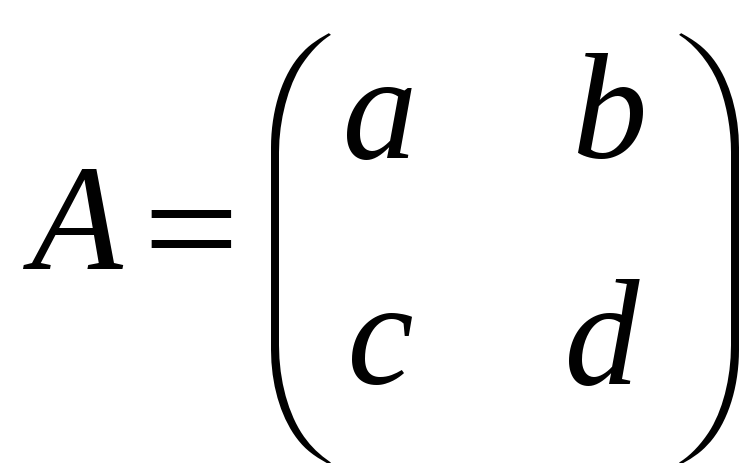 ,
,
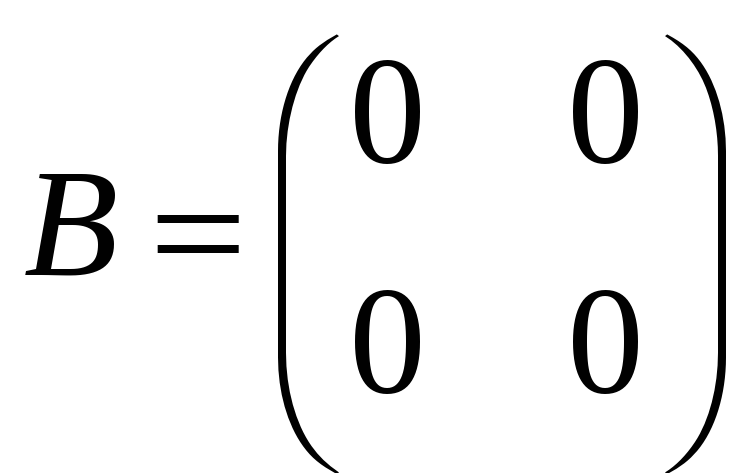 ;
г)
;
г)
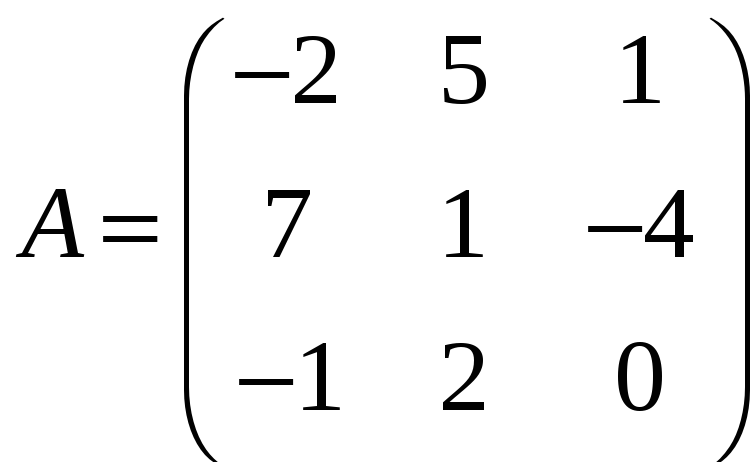 ,
,
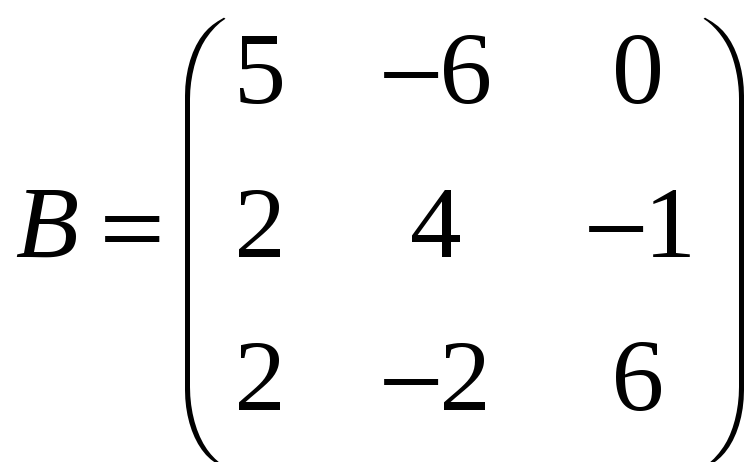 ;
;
д)
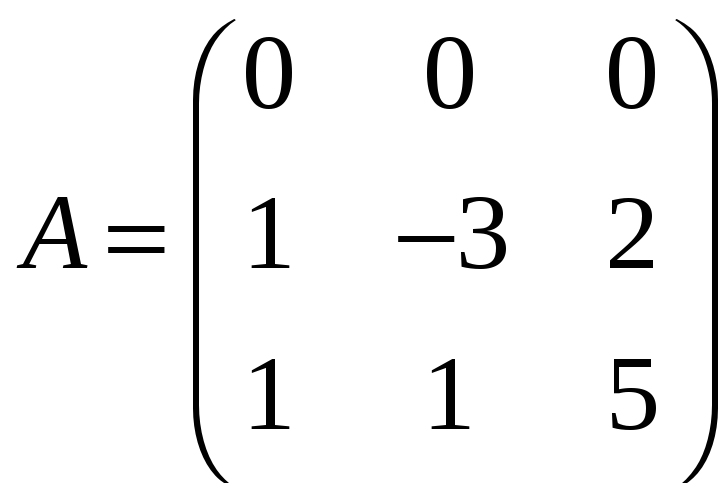 ,
,
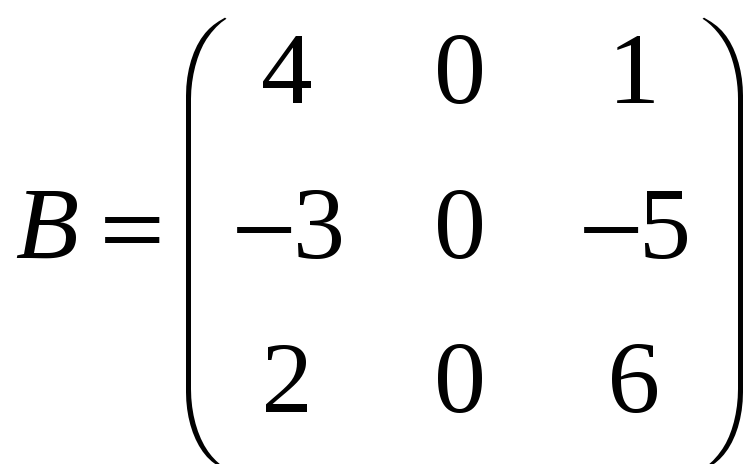 ;
е)
;
е)
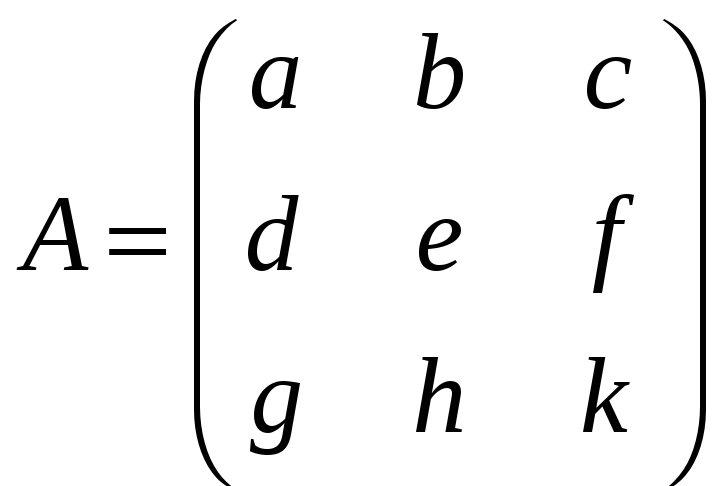 ,
,
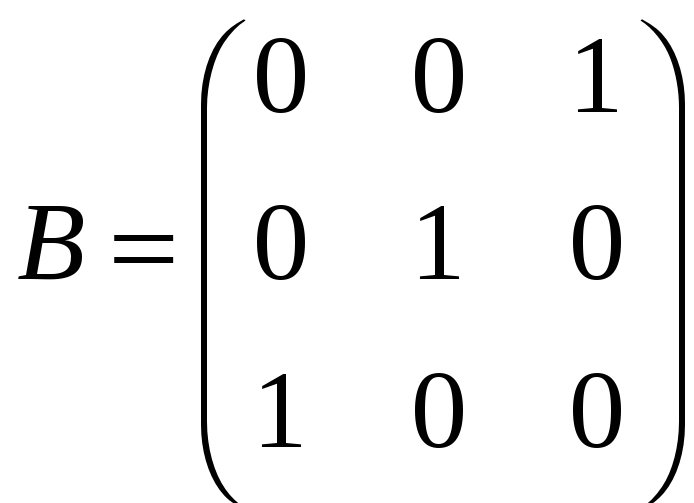 ;
;
є)
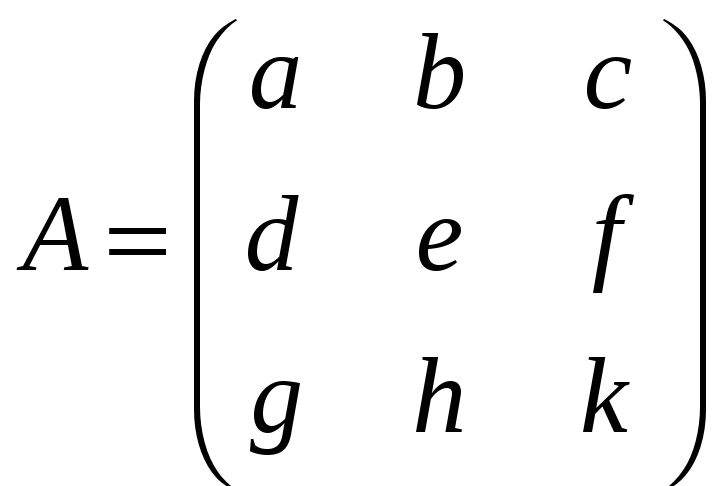 ,
,
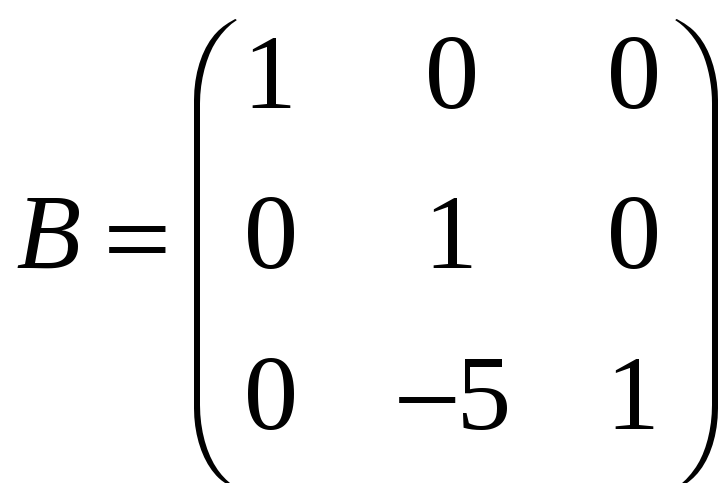 ;
ж)
;
ж)
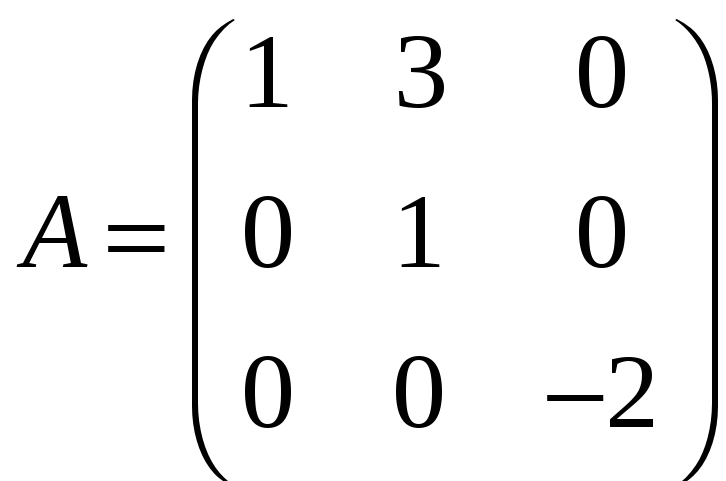 ,
,
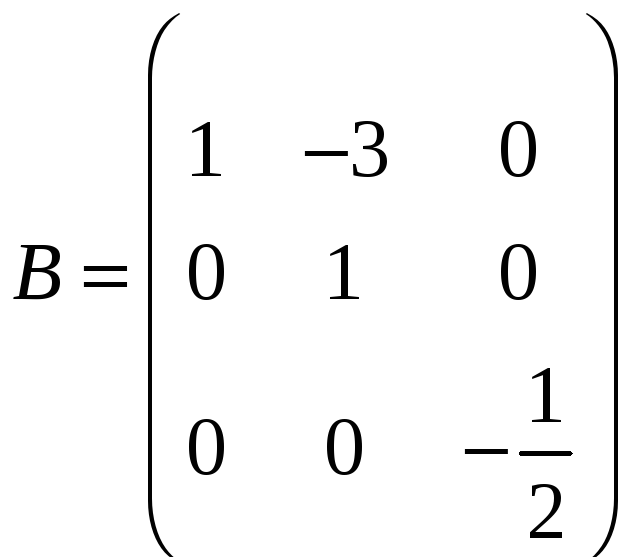 ;
;
з)
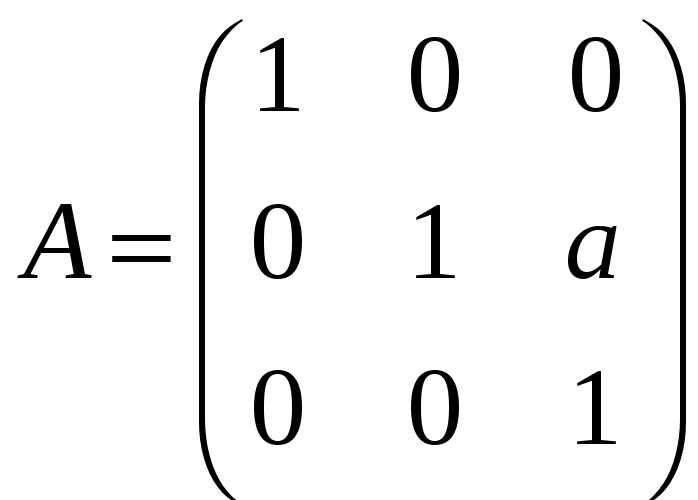 ,
,
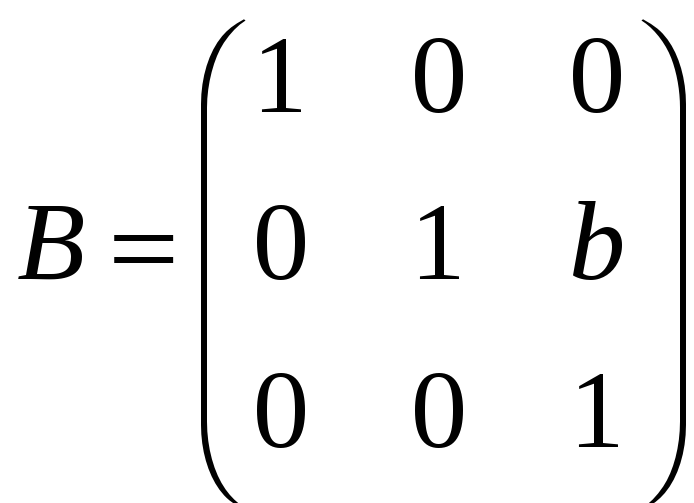 ;
і)
;
і)
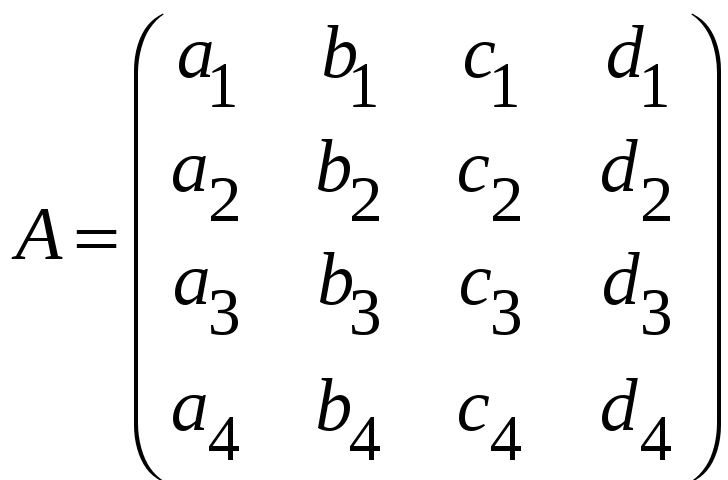 ,
,
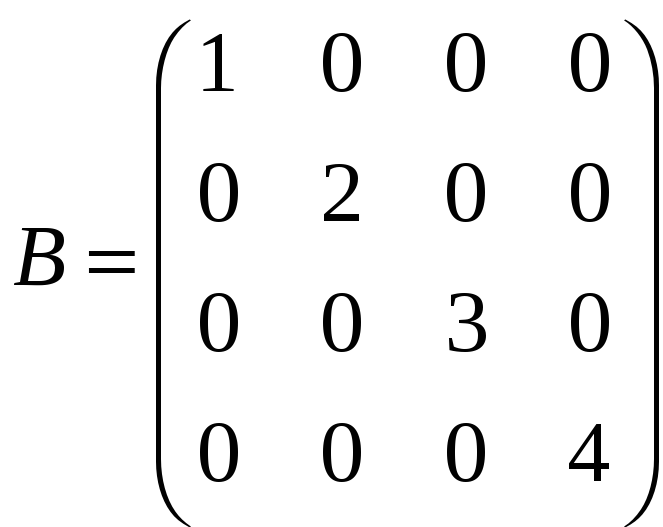 ;
к)
;
к)
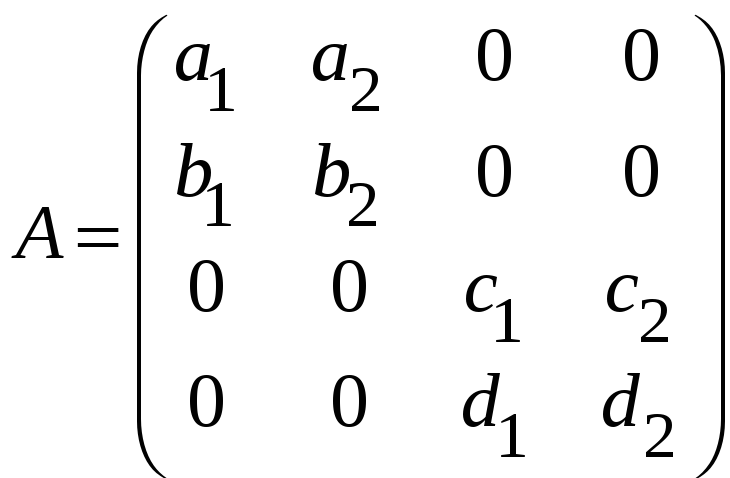 ,
,
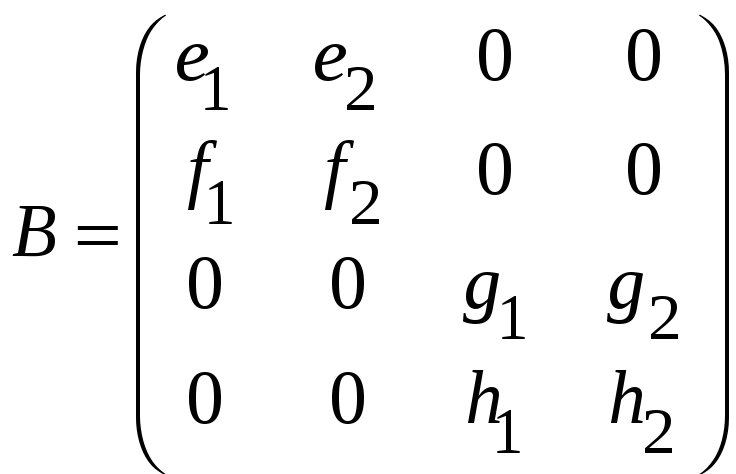 .
.
Задача
3.5.
Знайти
матрицю
![]() ,
якщо A
=
,
якщо A
=
 ,
,
B
=
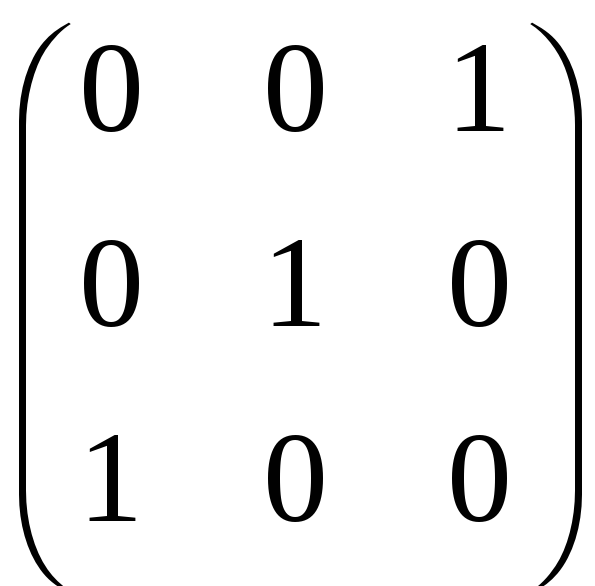 .
.
Задача
3.6.
Знайти
![]() (m
N),
якщо:
(m
N),
якщо:
а)
 ;
б)
;
б)
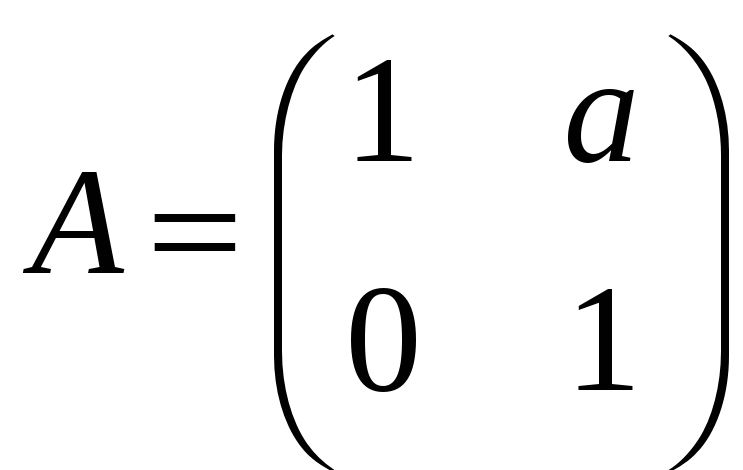 ;
в)
;
в)
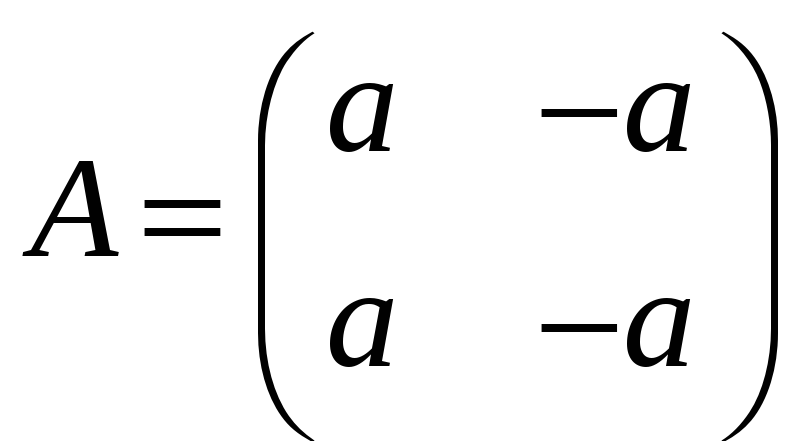 ;
г)
;
г)
 ;
;
д)
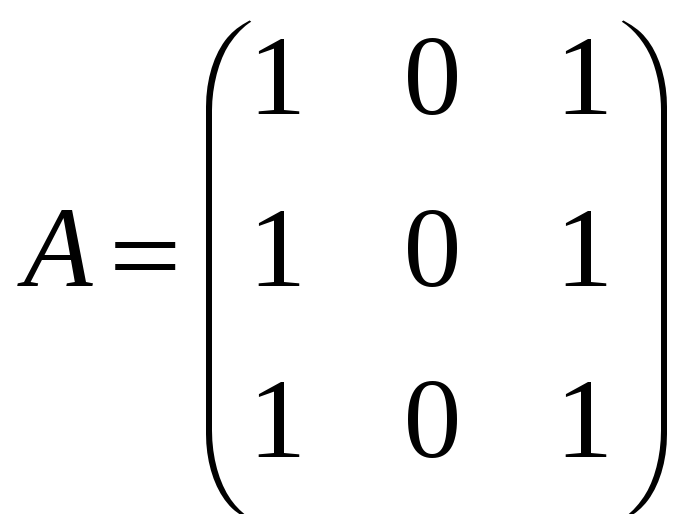 ;
е)
;
е)
 ;
є)
A =
;
є)
A =
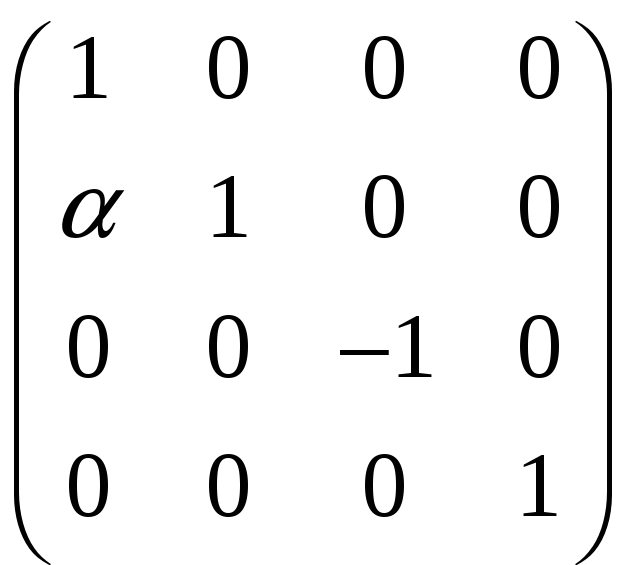 ;
;
ж)
A =
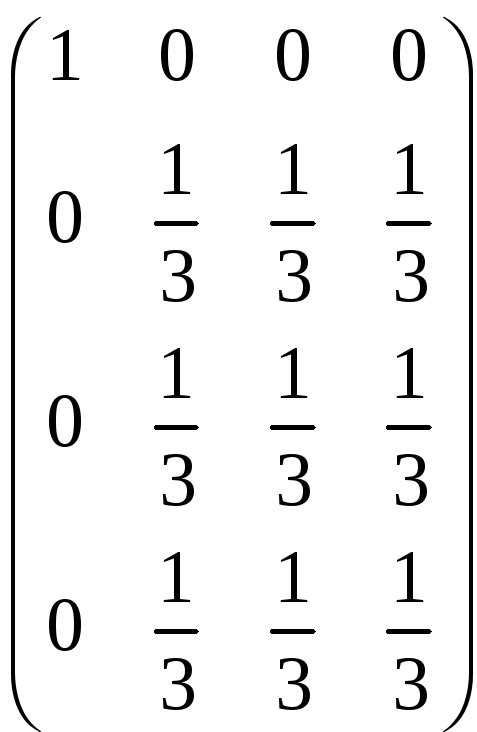 ;
з)
;
з)
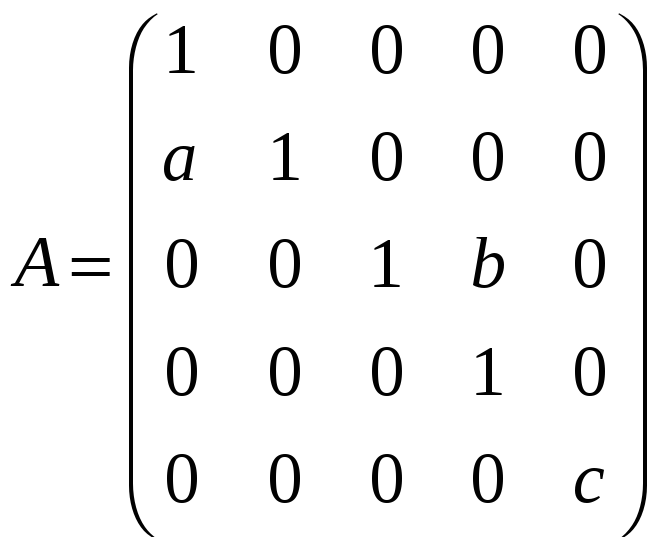 .
.
Задача 3.7. A і B квадратні матриці порядку n. Знайти добутки AB і BA.
а)
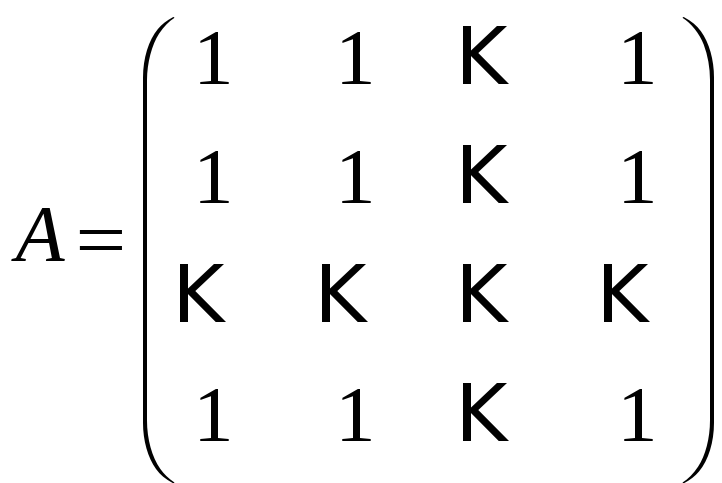 ,
B
= diag(1,
2,
,
n);
,
B
= diag(1,
2,
,
n);
б) A = diag( a1, a2, , an ), B =diag( b1, b2, , bn ).
Задача
3.8.
Знайти
![]() ,
якщо:
,
якщо:
а)
A
=
 ;
б)
A
=
;
б)
A
=
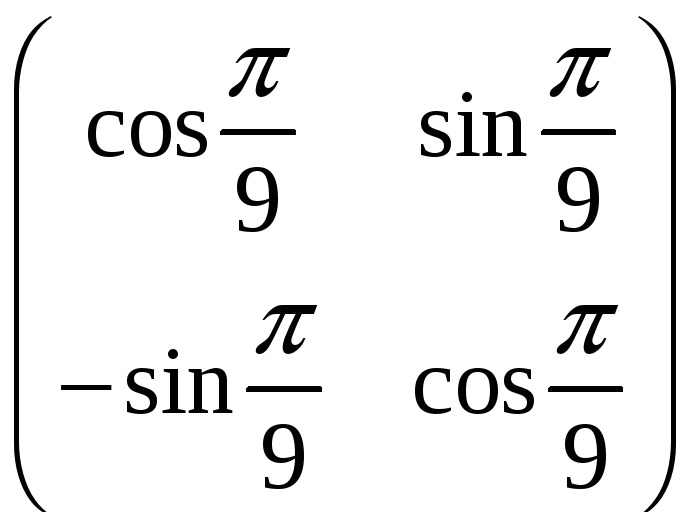 .
.
Задача
3.9.
Знайти
найменше натуральне число k,
таке що![]() .
.
а)
A
=
 ;
б)
A
=
;
б)
A
=
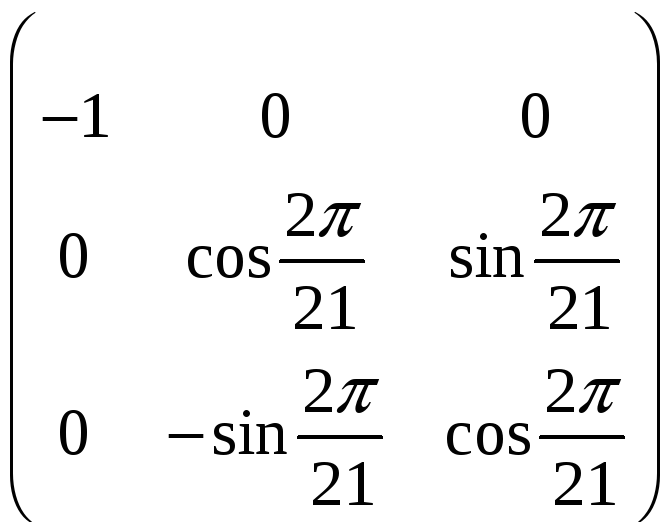 ;
;
в)
A
=
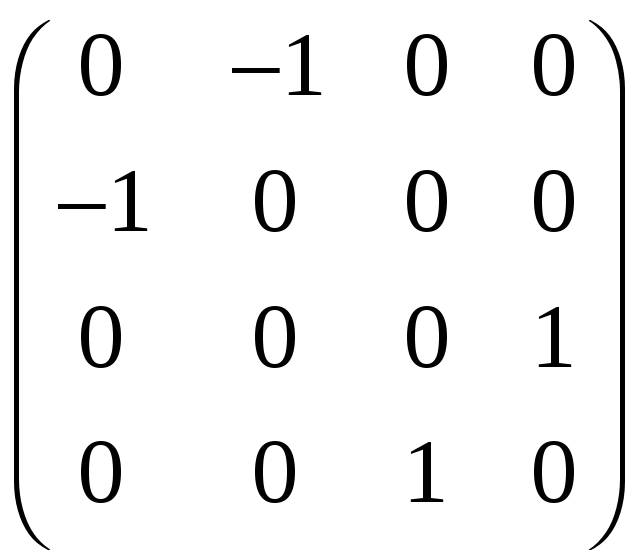 ;
г)
A =
;
г)
A =
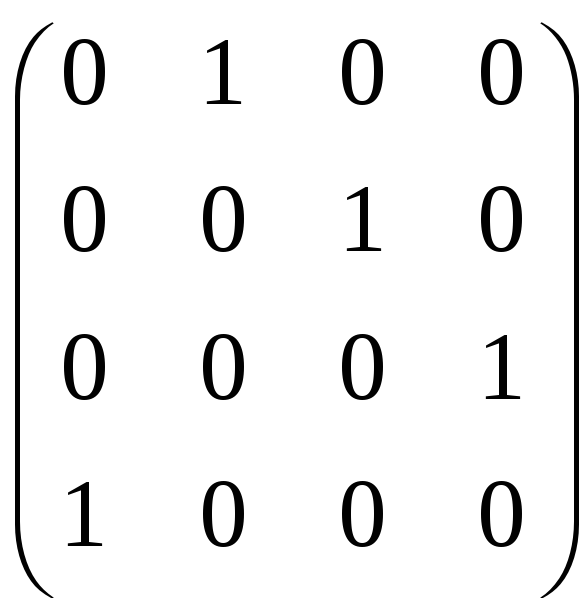 .
.
Задача
3.10.
Навести приклад неодиничної квадратної
матриці A
порядку
2, такої, що
![]() .
.
Задача
3.11.
Довести,
що для будь-яких
натуральних
чисел
n
і
m
існує
неодинична
квадратна матриця A
n-го
порядку, така, що
![]() .
.
Задача
3.12.
Знайти
значення многочлена
![]() від
матриці A.
від
матриці A.
а)
![]() ,
,
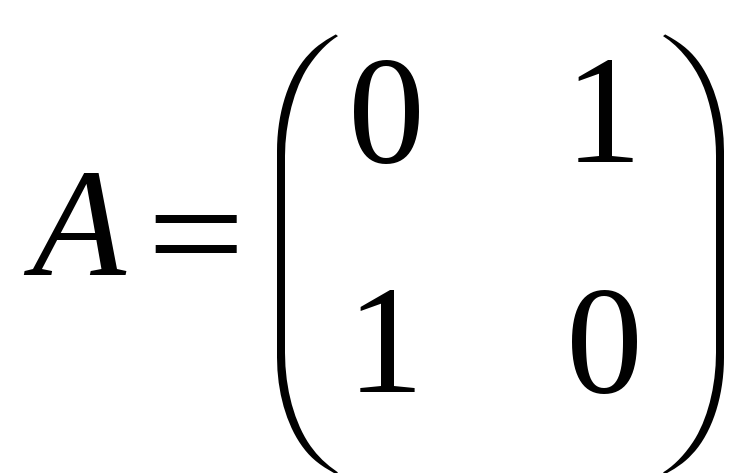 ;
б)
;
б)
![]() ,
,
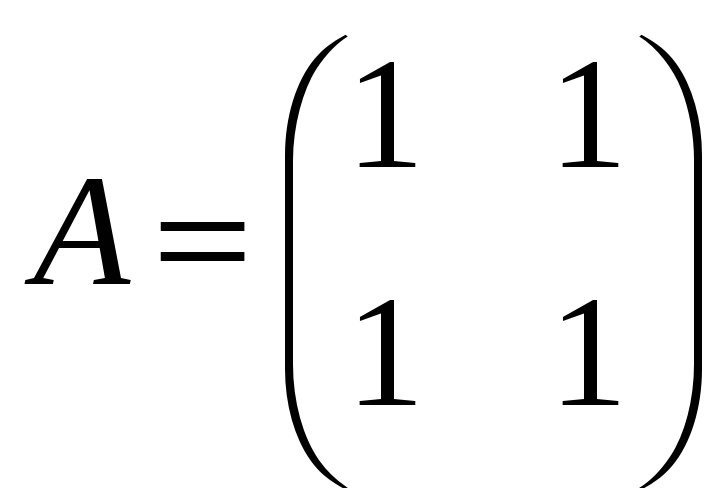 ;
;
в)
![]() ,
,
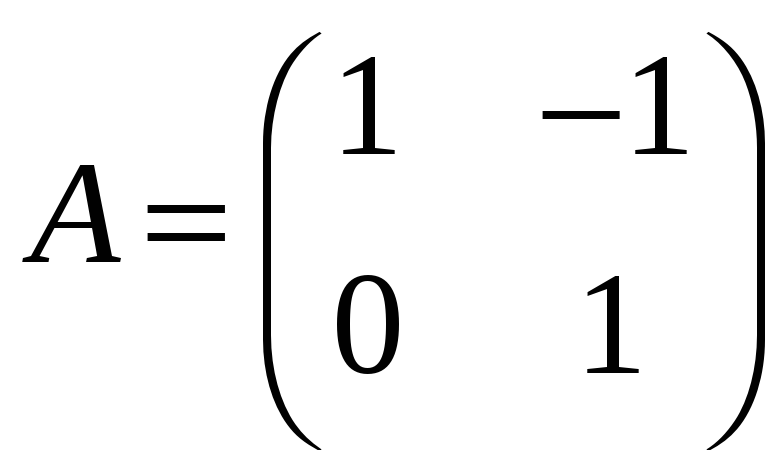 ;
;
г)
![]() ,
,
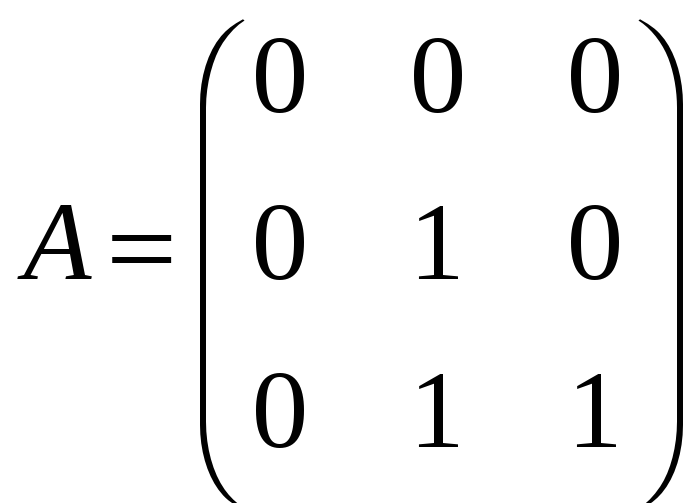 .
.
Задача 3.13. Навести приклад двох ненульових квадратних матриць A і B, таких, що добуток AB дорівнює нульовій матриці.
Задача
3.14.
Навести приклад ненульової квадратної
матриці A,
такої, що
![]() дорівнює нульовій матриці при будь-якому
натуральному m
2.
дорівнює нульовій матриці при будь-якому
натуральному m
2.
Задача 3.15. Знайти множину всіх квадратних матриць, переставних з матрицею A.
а)
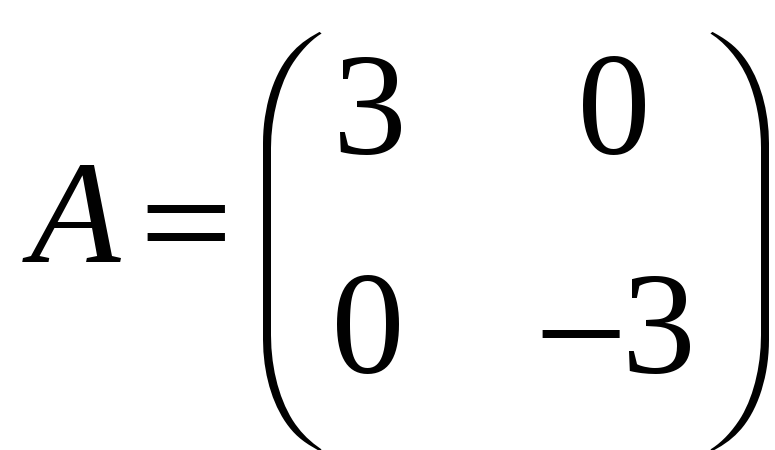 ;
б)
;
б)
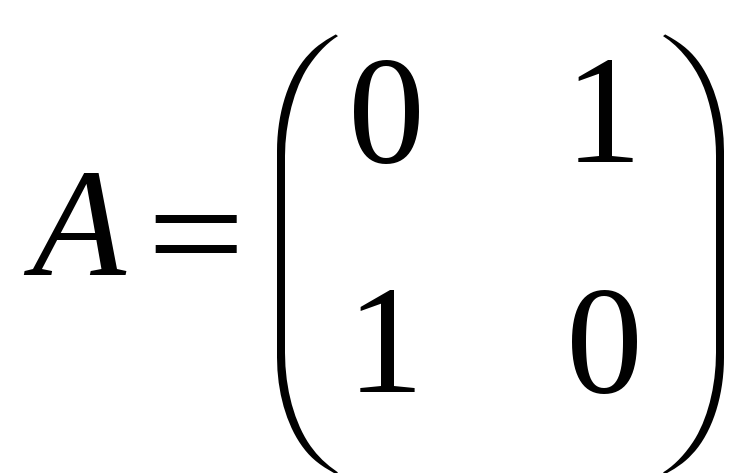 ;
в)
;
в)
 ;
г)
;
г)
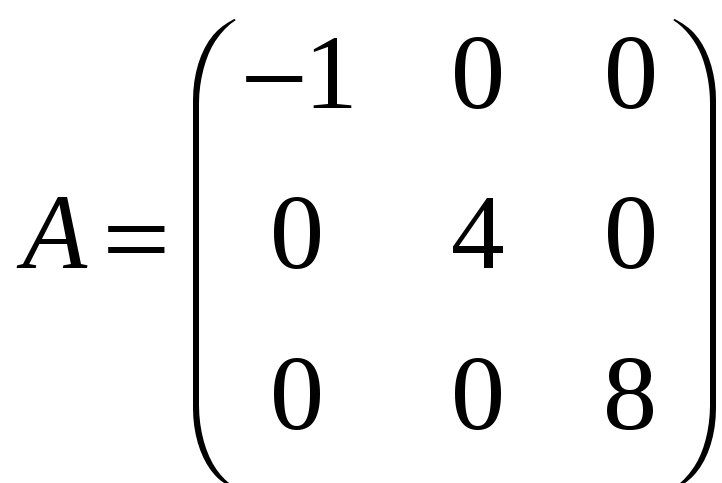 ;
;
д)
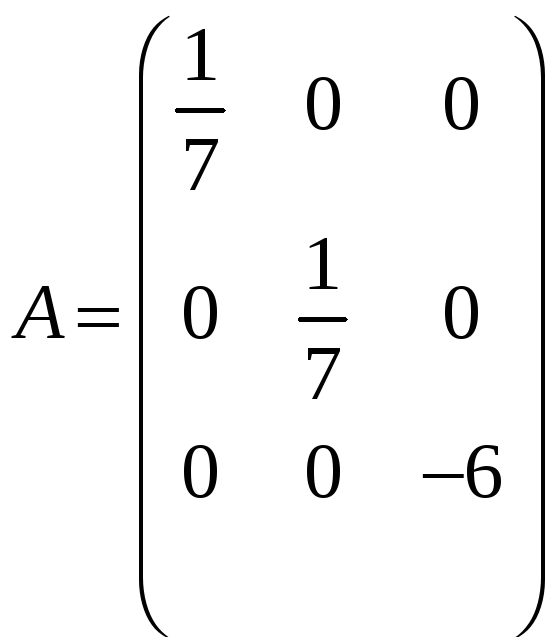 ;
е)
;
е)
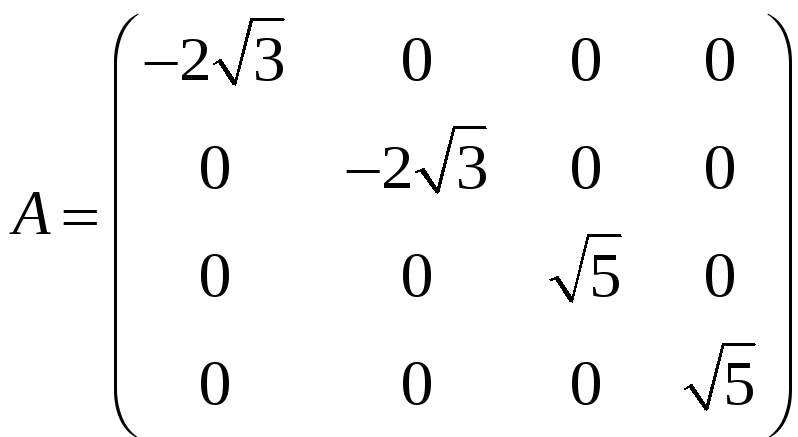 .
.
Задача 3.16. Нехай A – діагональна матриця порядку n, всі елементи головної діагоналі якої різні. Довести, що матриця B n-го порядку переставна з A тоді і тільки тоді, коли B є діагональною.
Задача 3.17. Нехай A – скалярна матриця n-го порядку. Знайти всі квадратні матриці, переставні з A.
Задача
3.18.
Нехай A
– квадратна матриця порядку 2, така, що
trA
=
0.
Довести,
що матриця
![]() є скалярною.
є скалярною.
Задача
3.19.
Елементи матриці
![]() визначені за правилом:
визначені за правилом:
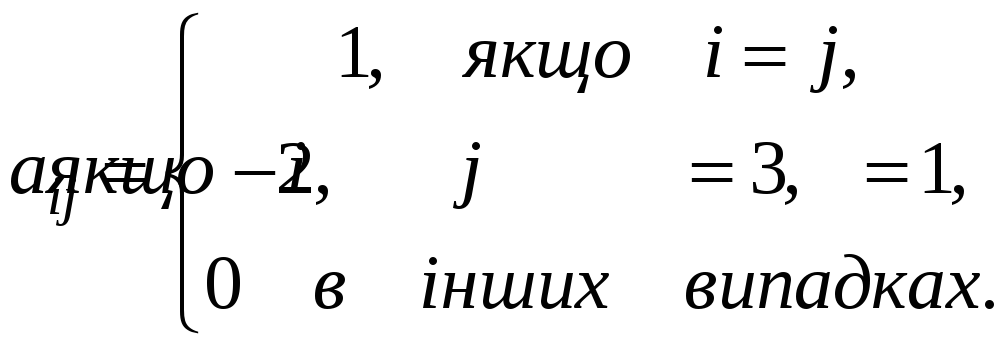
Знайти
елементи матриці B,
якщо
![]() .
.
Задача
3.20.
Елементи матриць
![]() і
і
![]() (n
2) визначені
за правилами
(n
2) визначені
за правилами

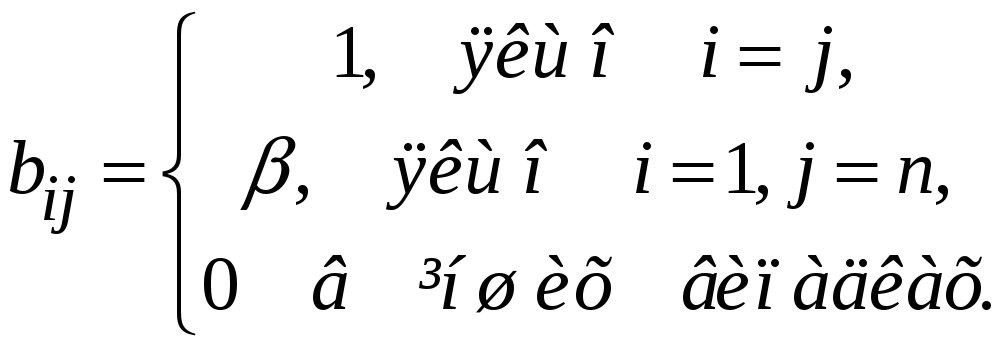
(![]() і
і
![]()
деякі дійсні числа).
Знайти
елементи матриць С
і
D,
якщо С
= AB,
деякі дійсні числа).
Знайти
елементи матриць С
і
D,
якщо С
= AB,
D = BA.
Задача
3.21.
Нехай
 .
Елементи матриці
.
Елементи матриці
![]() визначені за правилом
визначені за правилом
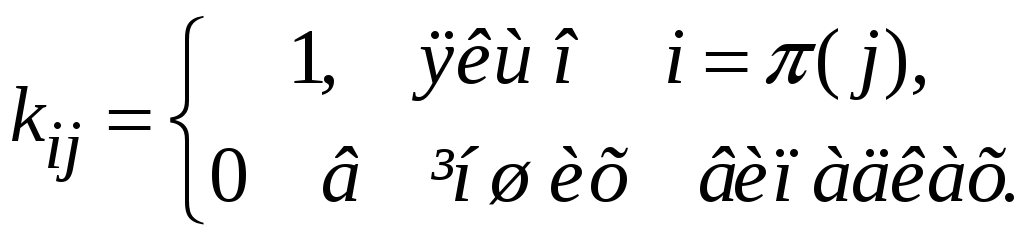
Знайти
найменше натуральне число m
таке,
що
![]() .
.
Задача 3.22. Як зміниться квадратна матриця A n-го порядку, якщо її помножити на матрицю В = diag ( b1, b2, , bn ): а) зліва; б) справа?
Задача 3.23. Як зміниться квадратна матриця A n-го порядку, якщо її помножити на матрицю
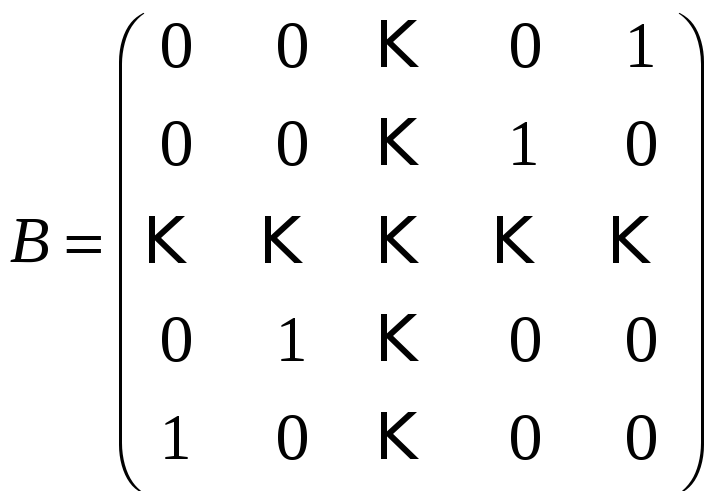 порядку
n:
порядку
n:
а) зліва; б) справа?
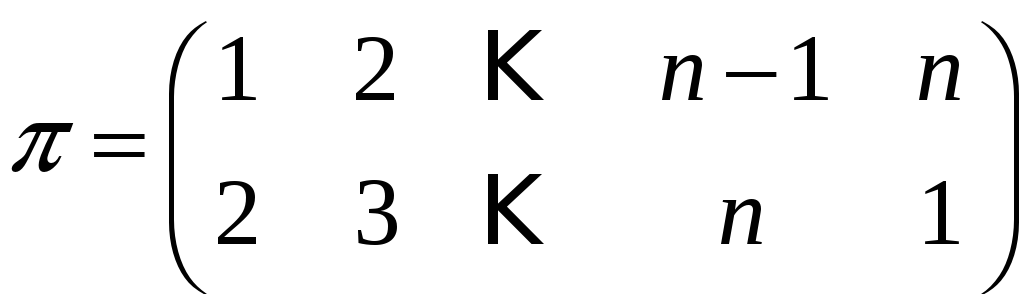
Задача
3.24. Нехай
![]() – деяка підстановка n-го
степеня. Елементи
матриці
– деяка підстановка n-го
степеня. Елементи
матриці
![]() визначені за правилами:
визначені за правилами:
 .
.
Довести,
що
![]() тоді і тільки тоді, коли
тоді і тільки тоді, коли
![]() .
.
Задача 3.25. Нехай A, B, C – квадратні матриці однакових порядків, detA = 2, detB = 3, detC = –1. Знайти det(ABCAt).
Задача
3.26.
Нехай
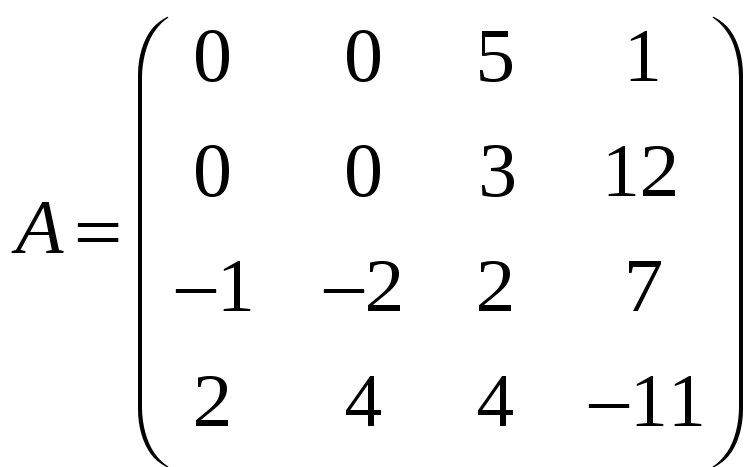 ,
B1,
B2,
,
Bn
– квадратні матриці четвертого порядку.
Знайти:
,
B1,
B2,
,
Bn
– квадратні матриці четвертого порядку.
Знайти:
а) detC, якщо С = AB1 + AB2 + ··· + ABn;
б) detD, якщо D = B1At + B2At + ··· + BnAt.
Задача 3.27. З’ясувати, які з добутків AB, BA є визначеними і знайти ті, що є визначеними.
а)
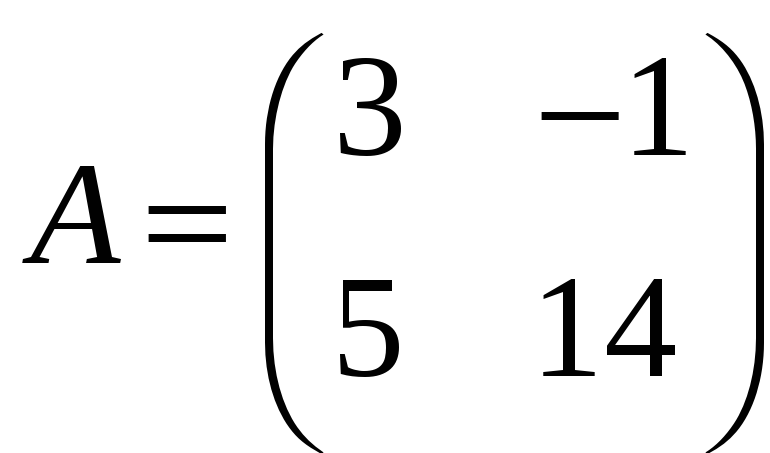 ,
,
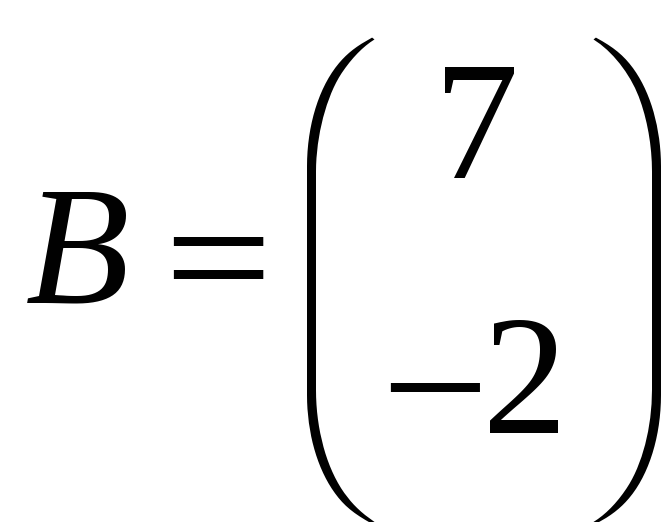 ;
б)
;
б)
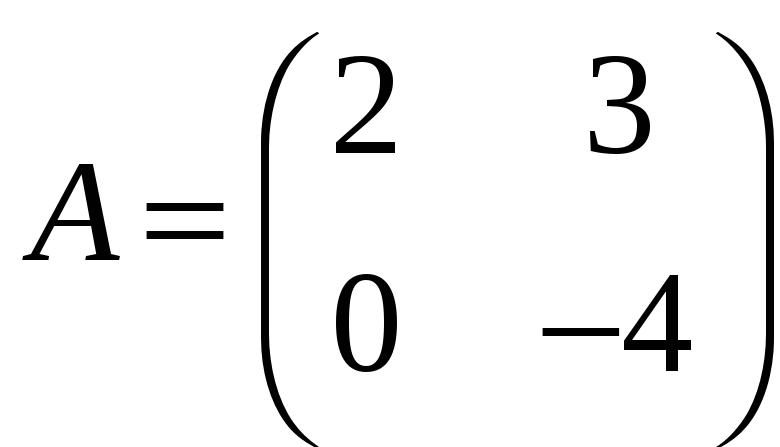 ,
,
 ;
;
в)
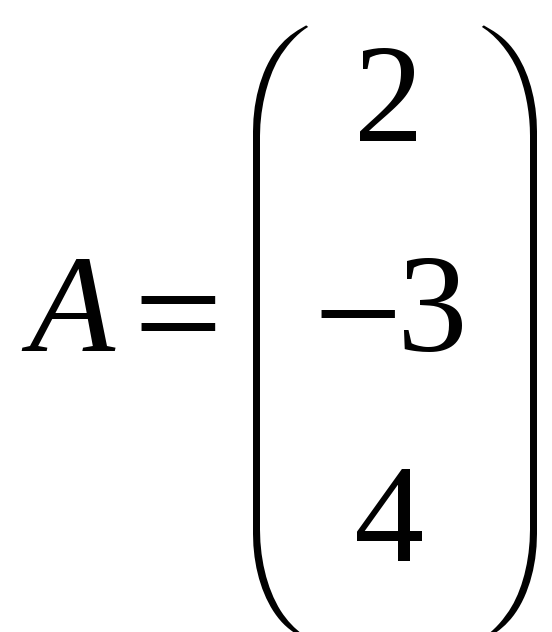 ,
,
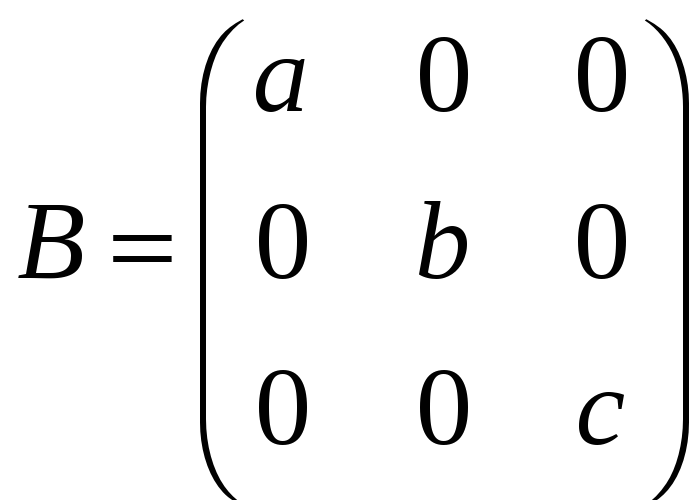 ;
г)
;
г)
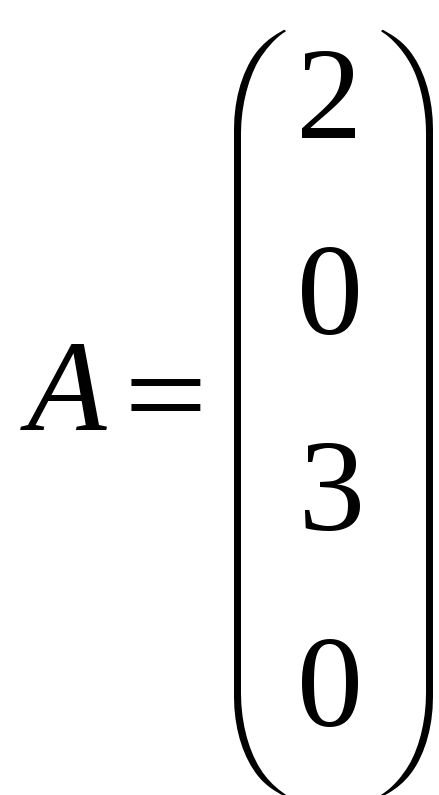 ,
,
![]() ;
;
д)
![]() ,
,
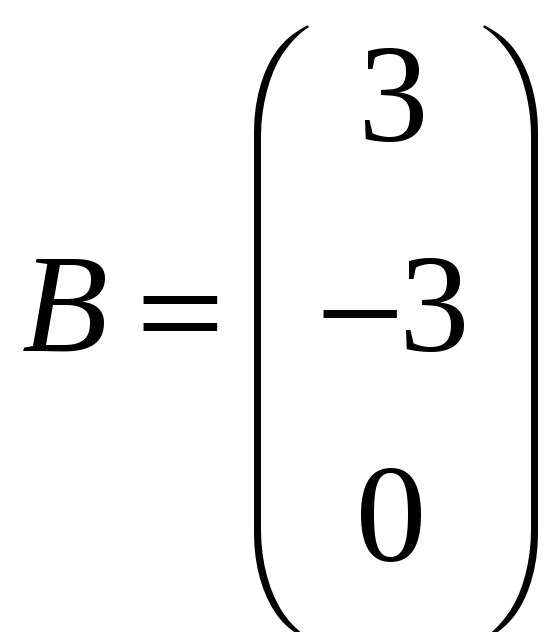 ;
е)
;
е)
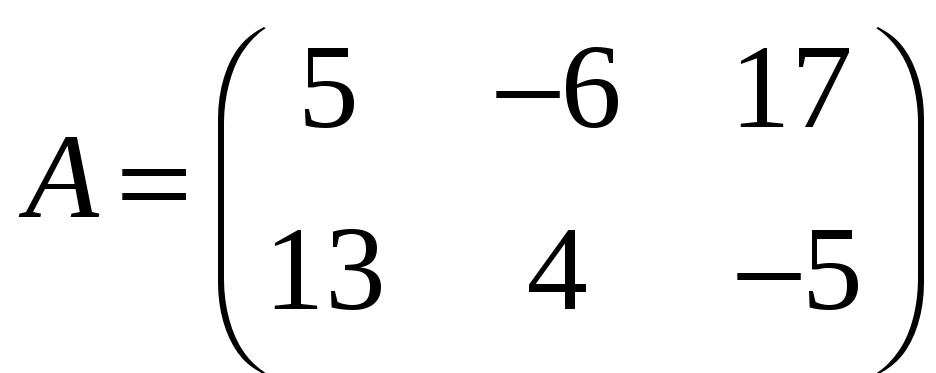 ,
,
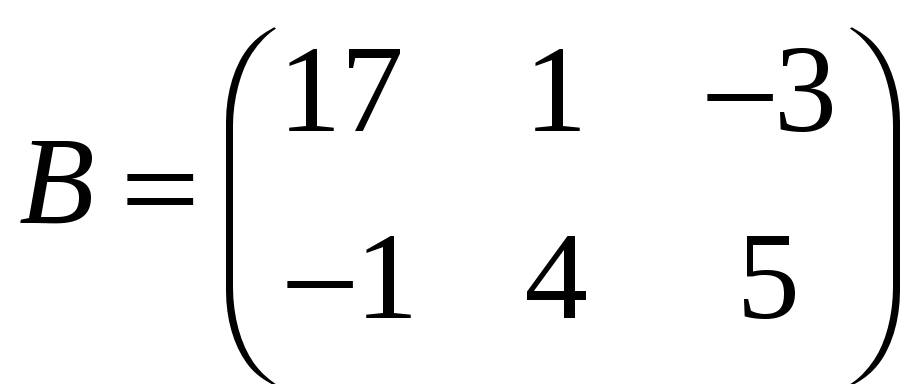 .
.
Задача
3.28.
Матриця
![]() має розмір 1
2, матриця
має розмір 1
2, матриця
![]() – 2
3, матриця
– 2
3, матриця
![]() –
–
3
4, і так далі, і насамкінець, матриця
![]() має розмір 100
101. З’ясувати, які з поданих добутків є
визначеними. Указати кількості рядків
і стовпців для тих добутків, що є
визначеними.
має розмір 100
101. З’ясувати, які з поданих добутків є
визначеними. Указати кількості рядків
і стовпців для тих добутків, що є
визначеними.
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() ;
д)
;
д)
![]() ;
е)
;
е)
![]() .
.
Задача 3.29. Як зміниться добуток AB матриць A і B, якщо:
а) переставити місцями k-й та m-й рядки матриці A?
б) k-й
рядок матриці A
помножити на число
![]() ?
?
в) до k-го рядка
матриці A додати
m-й рядок,
помножений на число
![]() ?
?
г) переставити місцями k-й та m-й стовпці матриці B?
д) k-й
стовпець матриці B
помножити на число
![]() ?
?
е) до k-го
стовпця матриці B додати m-й
стовпець, помножений на число
![]() ?
?
Задача 3.30. Довести, що коли добуток матриць AB визначений і в матриці A k-й рядок нульовий, то в матриці-добутку AB k-й рядок також нульовий. Чи справджується обернене твердження?
Задача 3.31. Довести, що коли добуток матриць AB визначений і в матриці B k-й стовпець нульовий, то в добутку AB k-й стовпець також нульовий. Чи справджується обернене твердження?
Задача 3.32. Знайти матрицю, транспоновану до матриці A.
а)
![]() ;
б)
;
б)
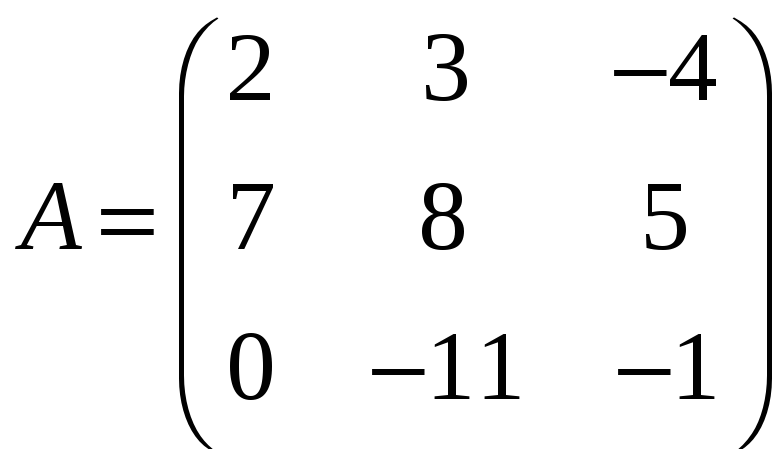 ;
в)
;
в)
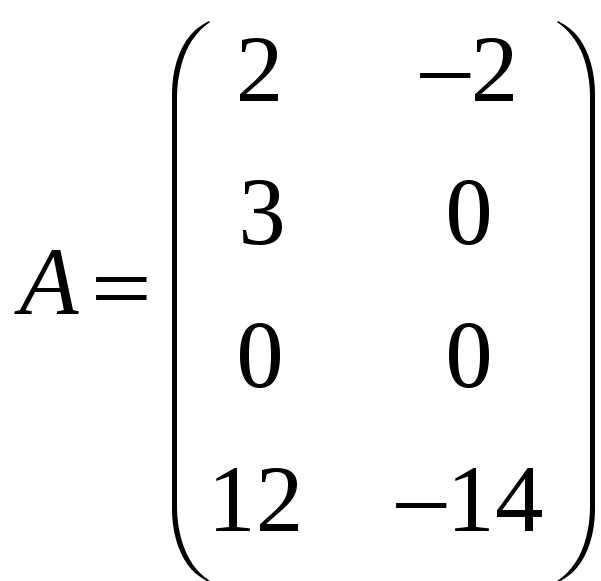 ;
г)
;
г)
![]() .
.
Задача 3.33. Довести, що будь-яка квадратна матриця може єдиним способом бути подана у вигляді суми симетричної та кососиметричної матриць.
Задача
3.34.
Довести,
що коли В – симетрична (кососиметрична)
матриця, то матриці
![]() ,
,
![]() ,
,
![]() є симетричними (кососиметричними).
є симетричними (кососиметричними).
Задача
3.35.
Нехай A
– матриця розміру k
n.
Довести, що добутки
![]() і
і
![]() є визначеними і вказати їх розміри.
Довести, що ці добутки є симетричними
матрицями.
є визначеними і вказати їх розміри.
Довести, що ці добутки є симетричними
матрицями.
Задача 3.36. Довести, що добуток двох симетричних (кососиметричних) матриць тоді і тільки тоді буде симетричною матрицею, коли ці матриці переставні.
Задача 3.37. З’ясувати, чи існує до матриці A обернена матриця. Якщо так, то знайти A–1.
а)
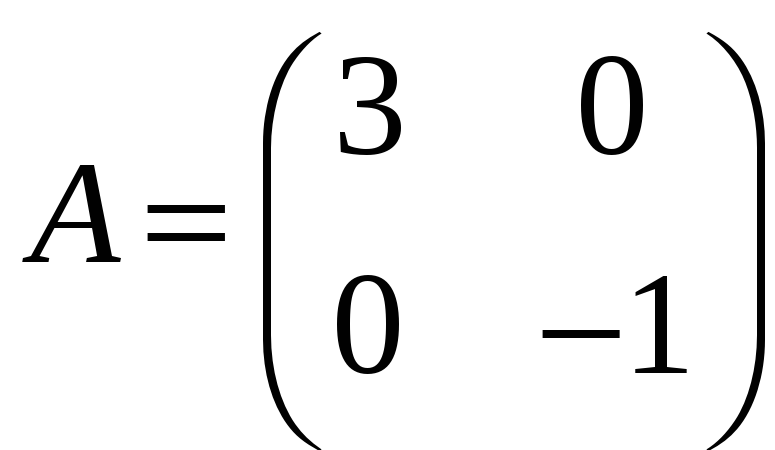 ;
б)
;
б)
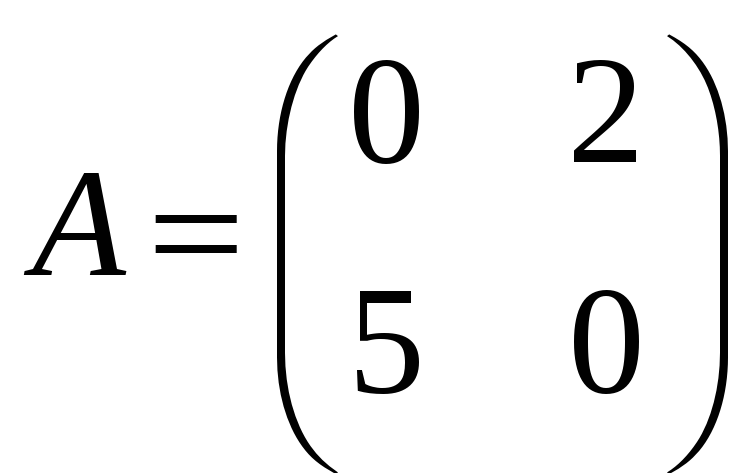 ;
в)
;
в)
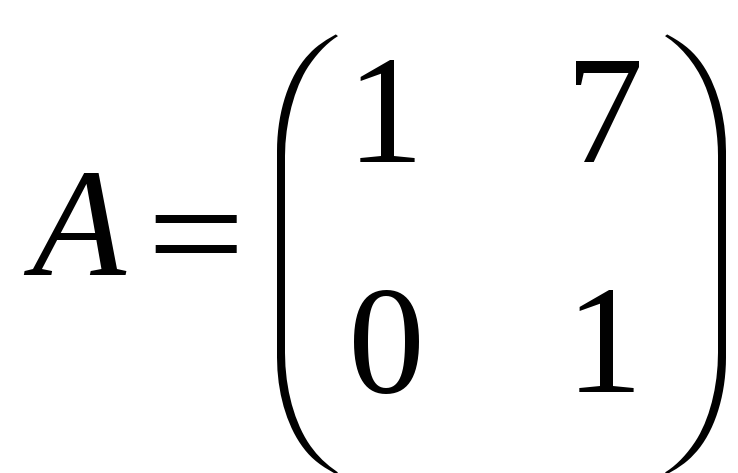 ;
г)
;
г)
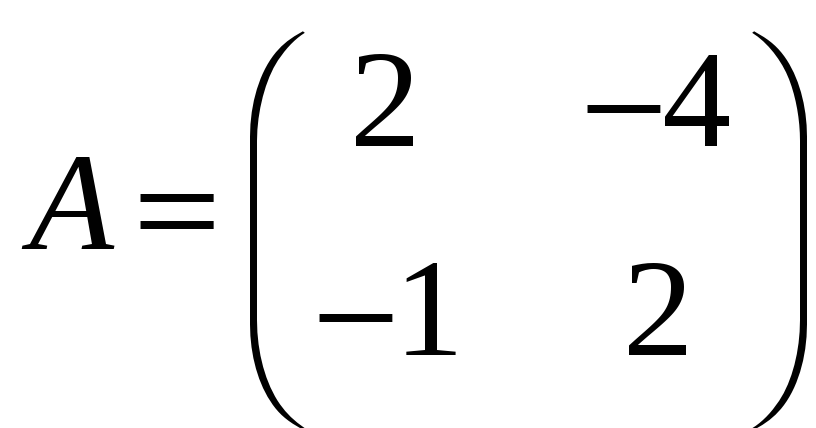 ;
;
д)
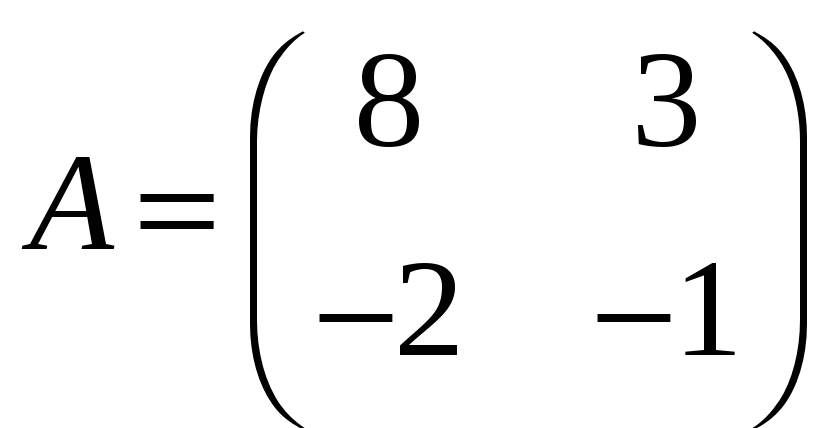 ;
е)
;
е)
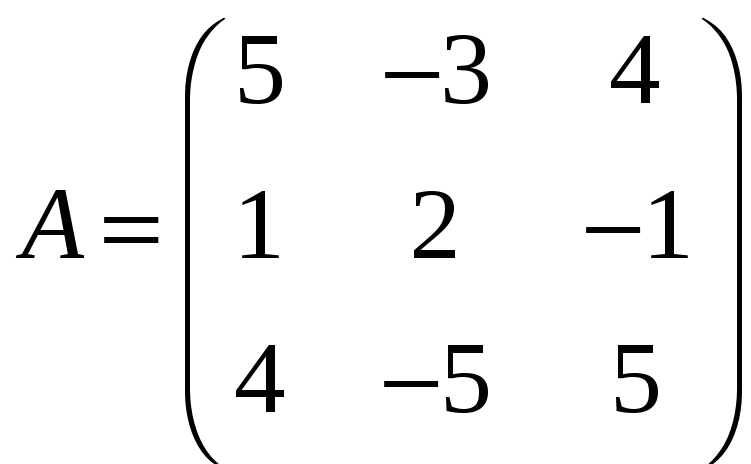 ;
є)
;
є)
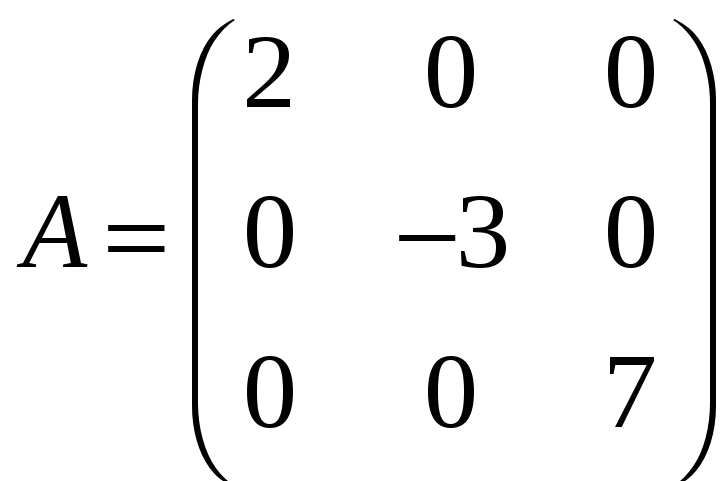 ;
ж)
;
ж)
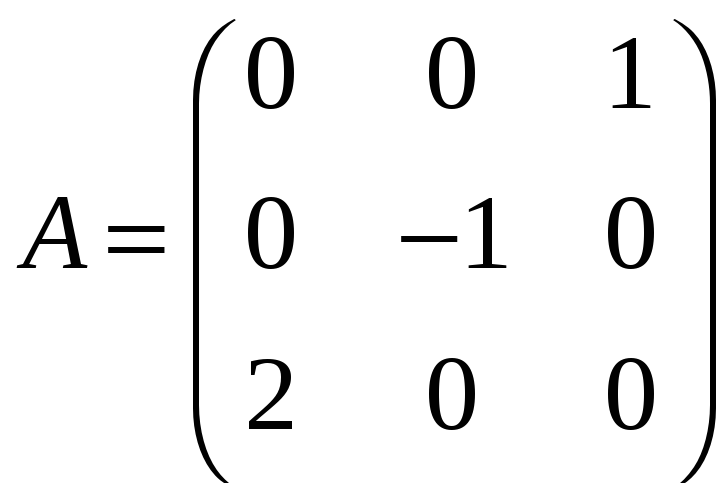 ;
з)
;
з)
 ;
і)
;
і)
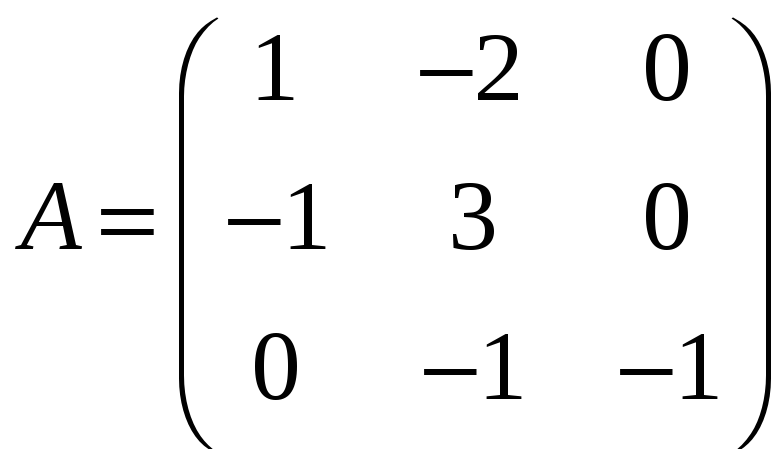 ;
к)
;
к)
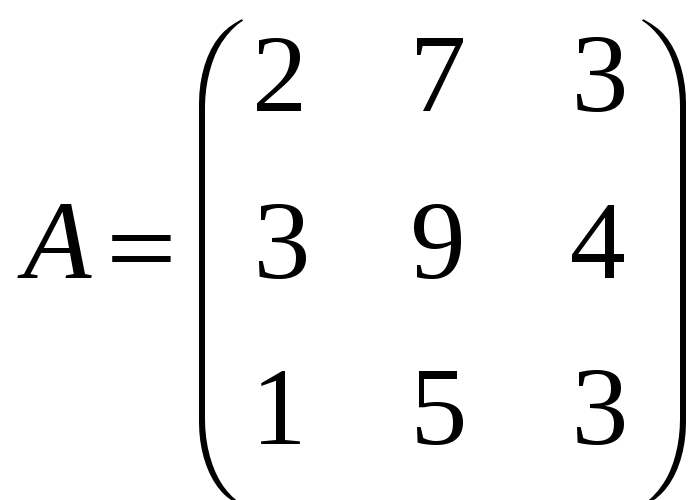 ;
;
л)
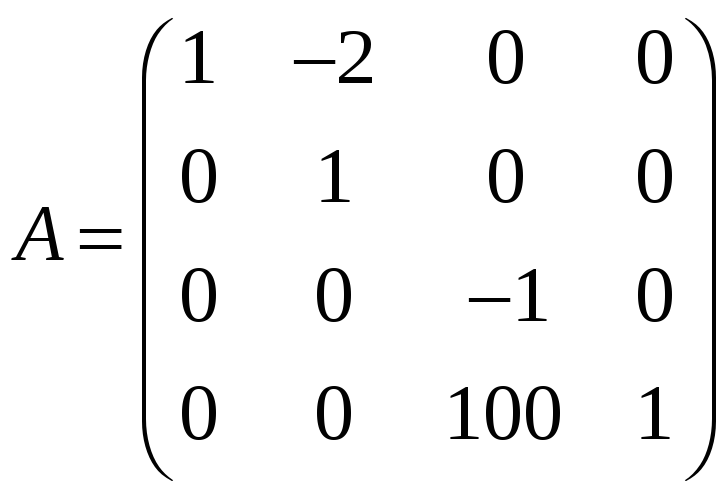 .
.
Задача 3.38. Нехай A = diag( a1, a2, , an ). За якої умови до матриці A існує обернена матриця і чому дорівнюють елементи матриці A–1, коли вона існує?
Задача 3.39. A – квадратна матриця, така що A = A–1. Знайти матрицю B, якщо B = (A + E)(A – E).
Задача 3.40. Знайти всі квадратні матриці A порядку n, такі що
A = A–1 і A15 = E.
Задача 3.41. Знайти A–1, якщо
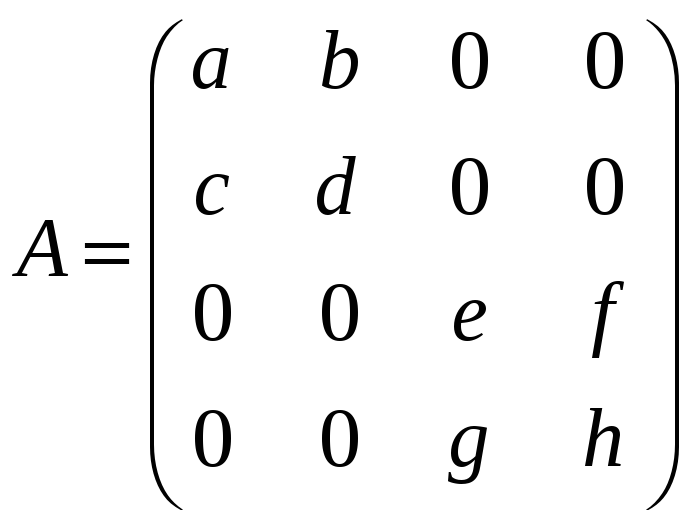 ,
,
причому ad – bc = fg – eh =1.
Задача 3.42. З’ясувати, які з поданих матриць мають обернені і за допомогою елементарних перетворень знайти обернені матриці:
а)
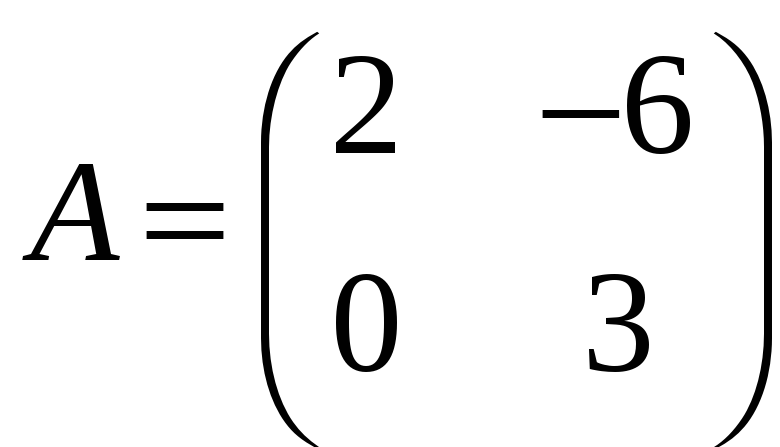 ;
б)
;
б)
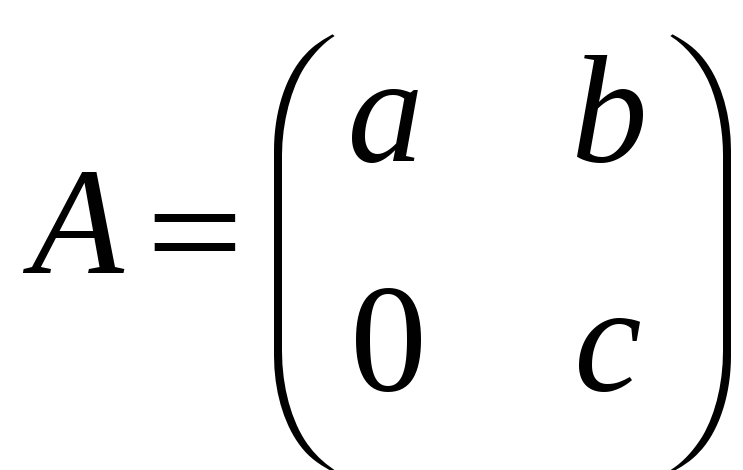 ;
в)
;
в)
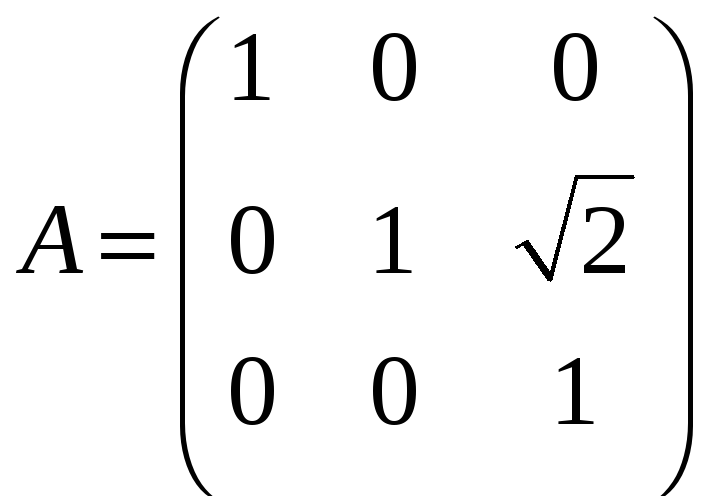 ;
г)
;
г)
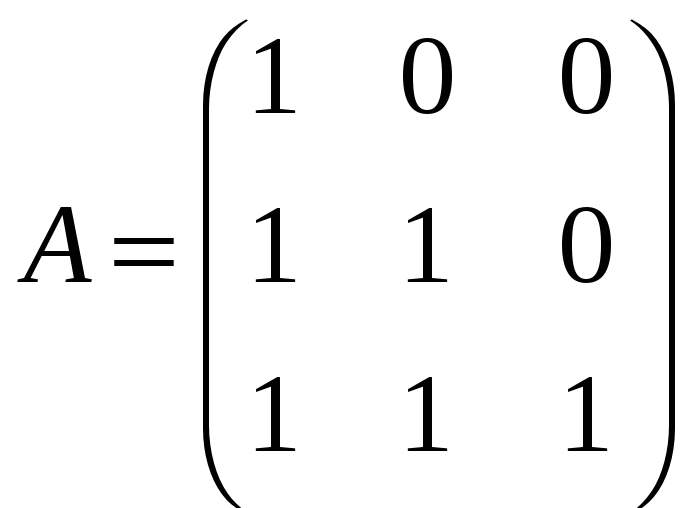 ;
;
д)
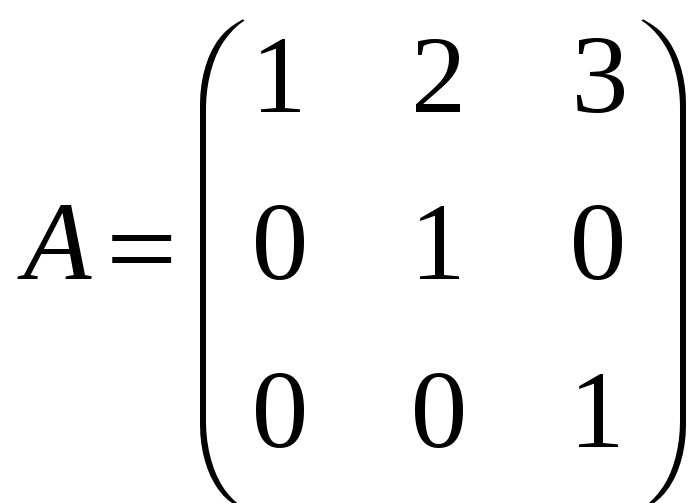 ;
е)
;
е)
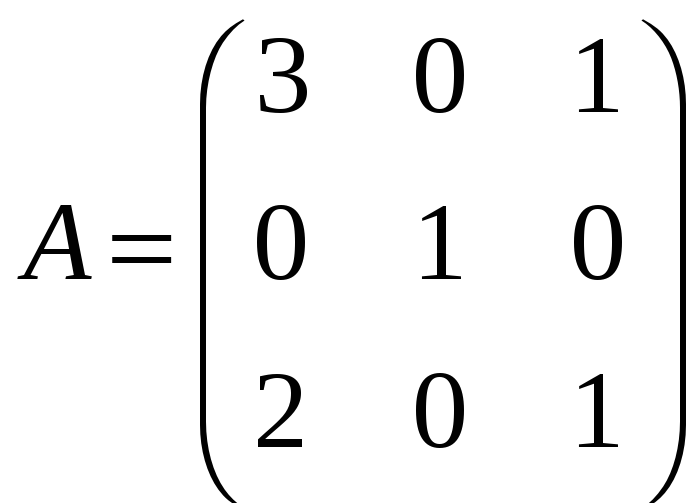 ;
є)
;
є)
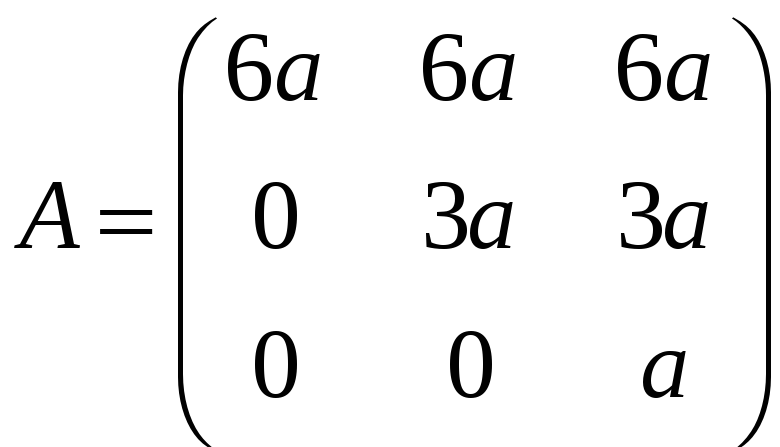 ;
;
ж)
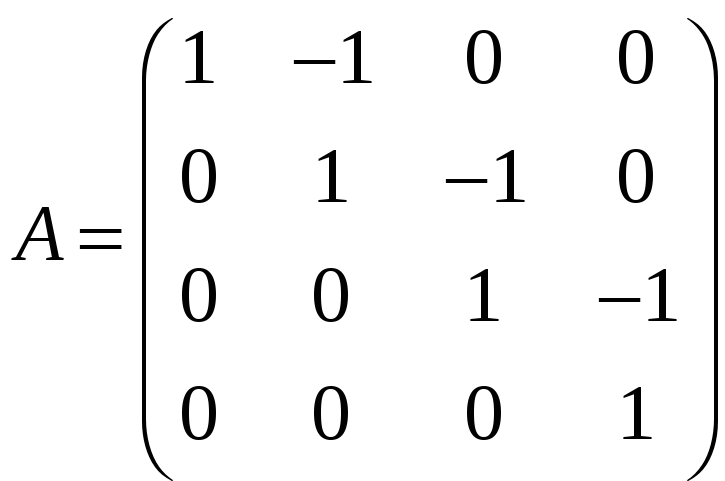 ;
з)
;
з)
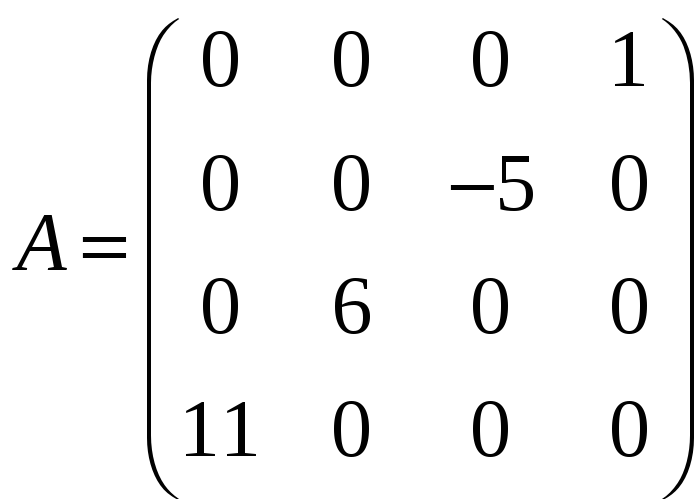 ;
і)
;
і)
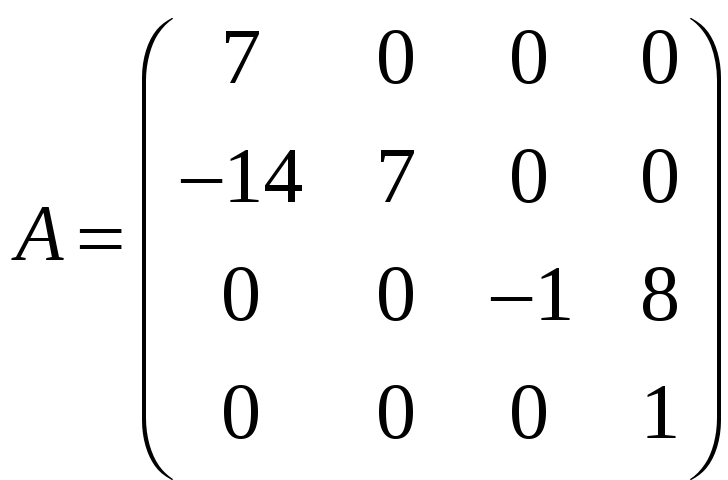 ;
;
к)
 ;
;
Матриці, подані нижче, мають порядок n.
л)
 ;
м)
;
м)
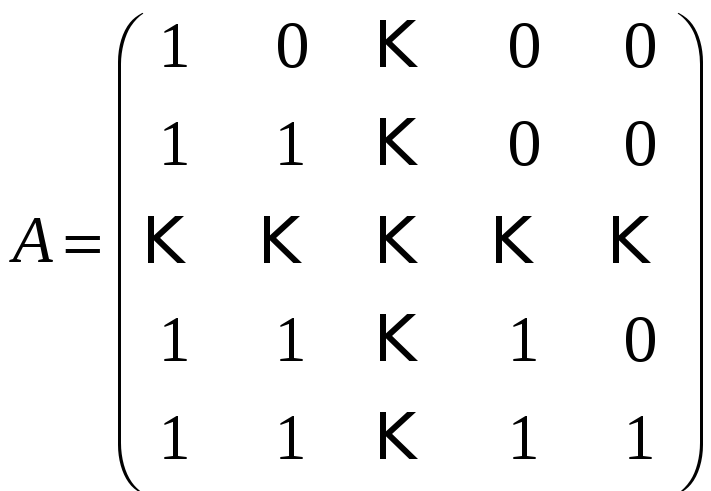 .
.
Задача 3.43. Як зміниться обернена матриця A–1, якщо:
а) у матриці A k-й та m-й стовпці переставити місцями?
б) у матриці A k-й та m-й рядки переставити місцями?
в)
у матриці A
k-й
стовпець помножити на число
![]() ?
?
г)
у матриці A
до k-го
рядка додати m-й
рядок, помножений на число
![]() ?
?
Задача 3.44. Розв’язати матричні рівняння:
а)
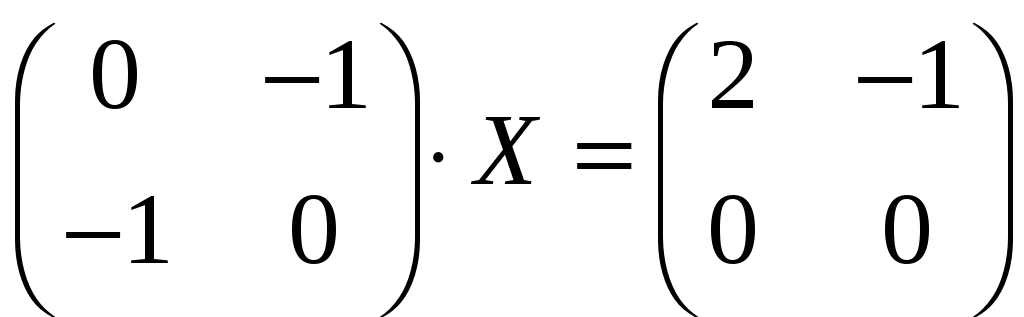 ;
б)
;
б)
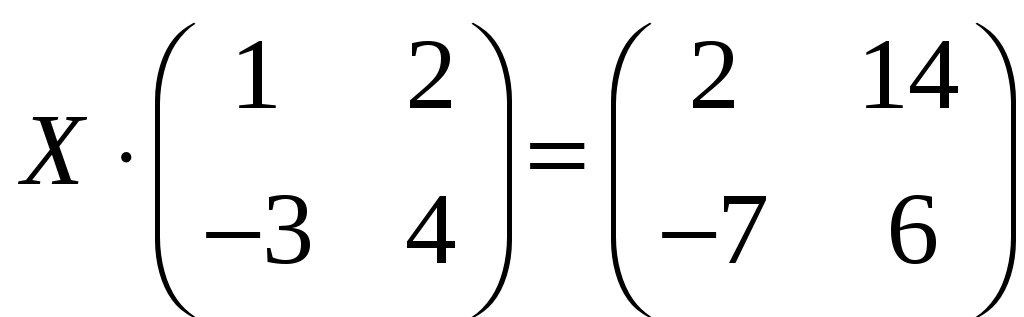 ;
;
в)
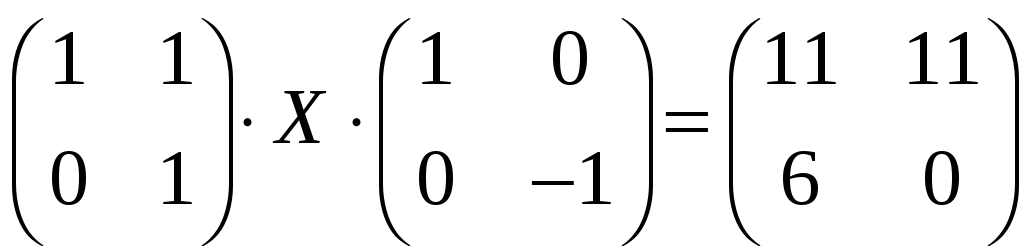 ;
;
г)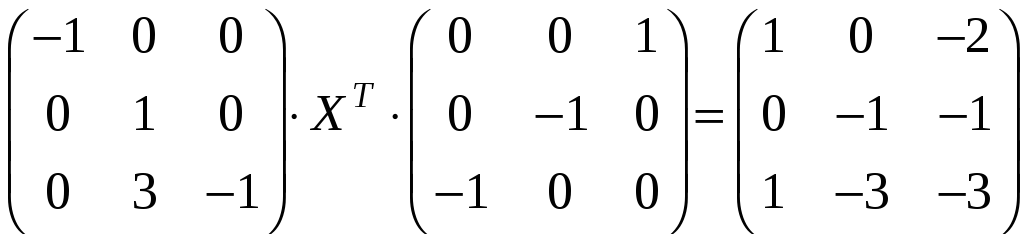 .
.
Відповіді
1.1.
перестановки із
а),
г) –
парні,
із б), в), д) – непарні. 1.2.
перестановки
із
а),
б), в) –
непарні,
із г) – парна. 1.3.
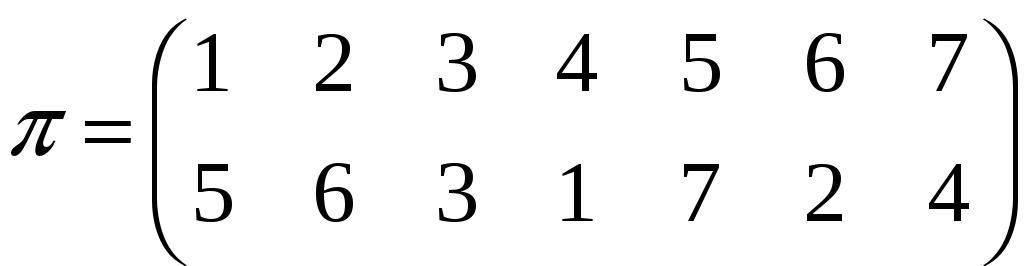 .
.
1.4.
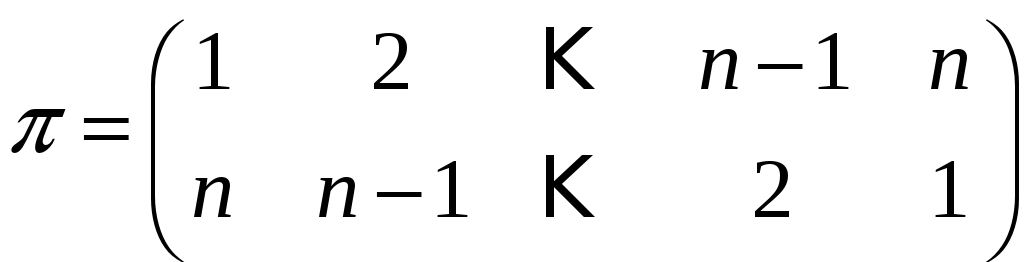 .
1.5.
а)
.
1.5.
а)
 ,
,
 .
1.6.
120.
1.7.
720.
.
1.6.
120.
1.7.
720.
1.8.
(n
–
k)!.
1.9.
б), в), г), є), з). 1.11.
![]() парна,
якщо число n
парне і непарна, якщо n
непарне. 1.12.
а)
парна,
якщо число n
парне і непарна, якщо n
непарне. 1.12.
а)
![]() є
парною, якщо число n
парне і непарною – у протилежному
випадку; б)
є
парною, якщо число n
парне і непарною – у протилежному
випадку; б)
![]() парна.
1.13.
а)
парна.
1.13.
а)
![]() є
парною, якщо n
парне і непарною– якщо n
непарне; б)
є
парною, якщо n
парне і непарною– якщо n
непарне; б)
![]() парна.
парна.
2.1. а) 7; б) 0; в) ab; г) –ab; д) 11; е) 0; є) 0; ж) –1; з) abc; і) –abc; к) –abc; л) 0;
м) ad – bc; н) adf; о) –abc. 2.2. а) не входить; б) входить із знаком «+»; в) входить із знаком «–»; г) входить із знаком «–»; д) не входить; е) входить із знаком «+»; є) входить із знаком «–». 2.3. (–1)n–1. 2.4. i = 3, j = 5. 2.5. i = j = 4, k = 3. 2.6. 0. 2.7. –1, 0 або 1. 2.8. а) 24; б) –30; в) –144; г) 0; д) 1; е) abcd; є) –abcd; ж) 0. 2.9. а) 1;
б)
(–1)n;
в)
n!;
г)
0;
д)
0;
е)
![]() ;
є)
;
є)
![]() ;
;
ж)
![]() ;
з)
0.
2.10.
(–1)n–1·2n.
2.12.
Не зміниться. 2.13.
Змінить знак.
2.14. Помножиться
на
;
з)
0.
2.10.
(–1)n–1·2n.
2.12.
Не зміниться. 2.13.
Змінить знак.
2.14. Помножиться
на
![]() .
2.15.
Помножиться на (–1)n.
2.16.
Змінить знак. 2.17.
Помножиться на 3.
2.18.
а)
.
2.15.
Помножиться на (–1)n.
2.16.
Змінить знак. 2.17.
Помножиться на 3.
2.18.
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() .
2.19.
.
2.19.
![]() .
2.21.
а)
4;
б)
240;
в)
21;
г)
7;
д)
.
2.21.
а)
4;
б)
240;
в)
21;
г)
7;
д)
![]() ;е)
44;
є)
3;
ж)
280;
з)
–
;е)
44;
є)
3;
ж)
280;
з)
–![]() ;
і)
;
і)
![]() .
2.23.
xn
+ (1)n+1yn.
2.25.
а)
52;
б)
6; в)
56;
г)
.
2.23.
xn
+ (1)n+1yn.
2.25.
а)
52;
б)
6; в)
56;
г)
![]() ;
д)
;
д)
![]() ;
;
е)
![]() ;
є)
;
є)
![]() ;ж)
;ж)
![]() ;
з)
n
+ 1;
і)
;
з)
n
+ 1;
і)
![]() .
.
2.26.
1.
2.27.
![]() .
3.1.
а)
.
3.1.
а)
 ;
б)
;
б)
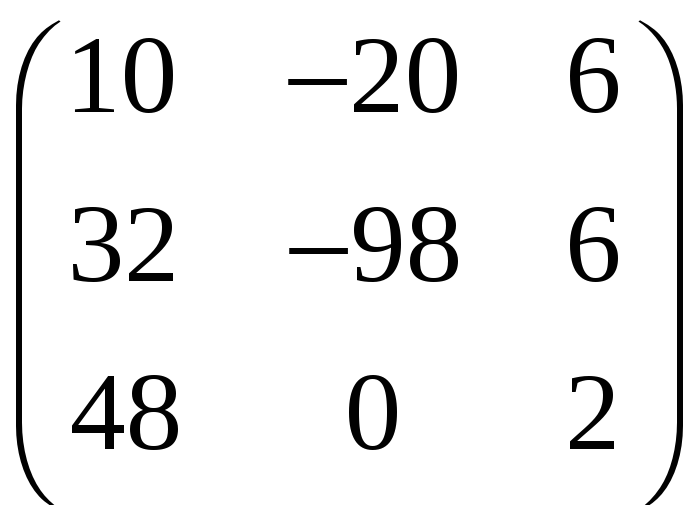 ;
в)
;
в)
 ;
г)
;
г)
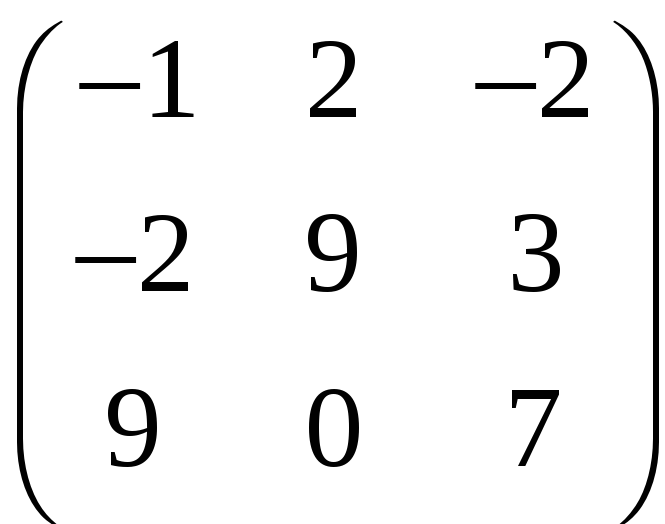 .
3.2.
а)
.
3.2.
а)
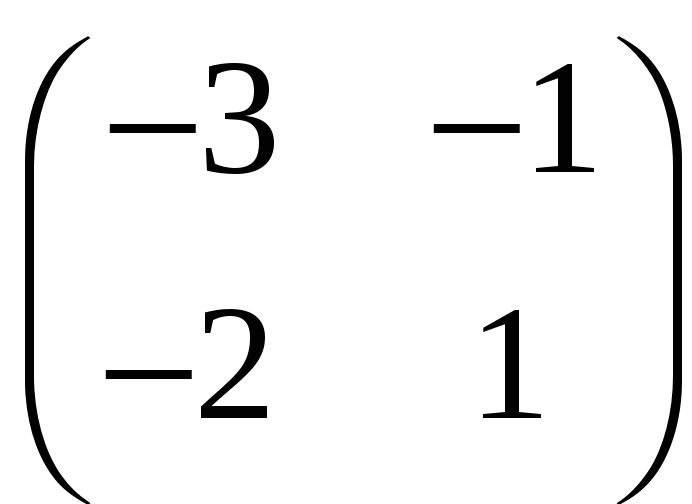 ;
б)
;
б)
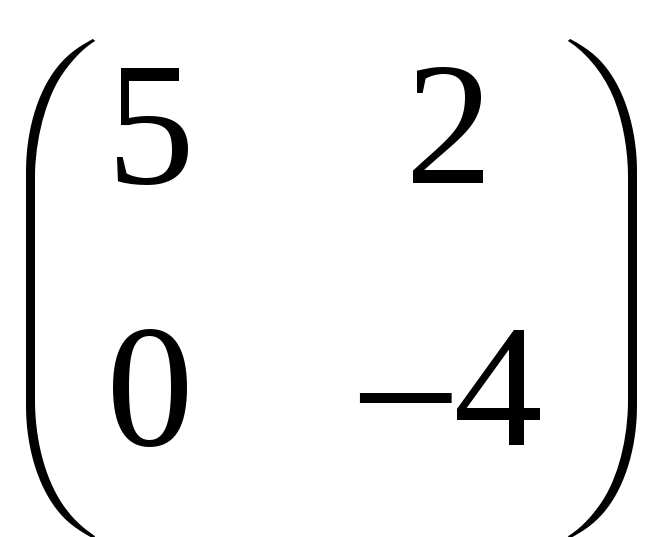 ;
в)
;
в)
![]() ;
г)
;
г)
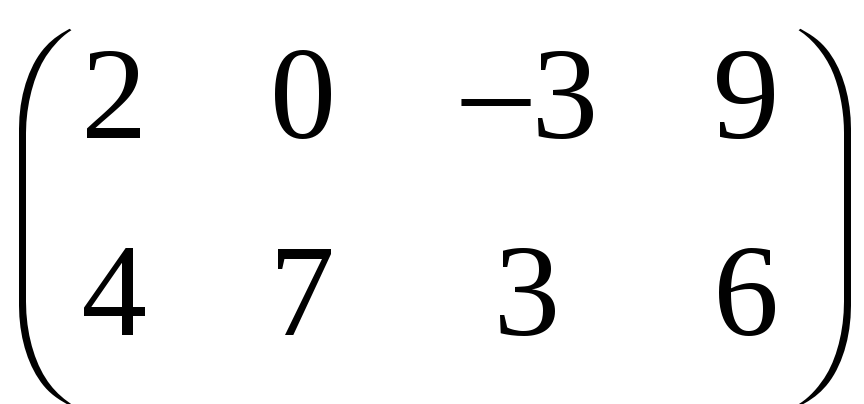 ;
;
д)
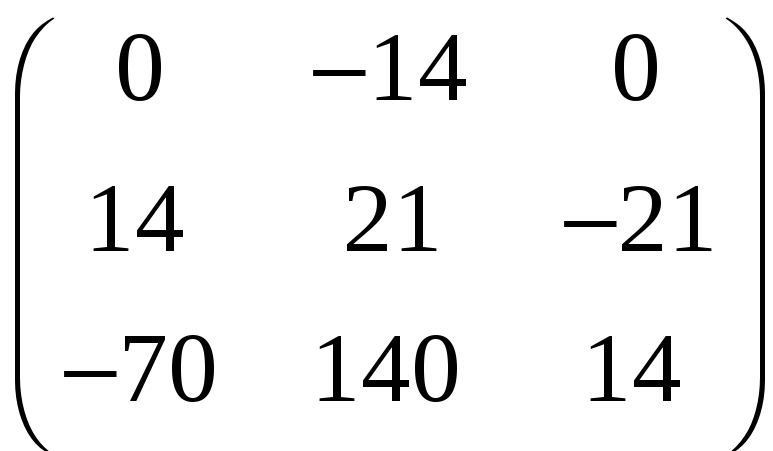 .
3.3.
а)
.
3.3.
а)
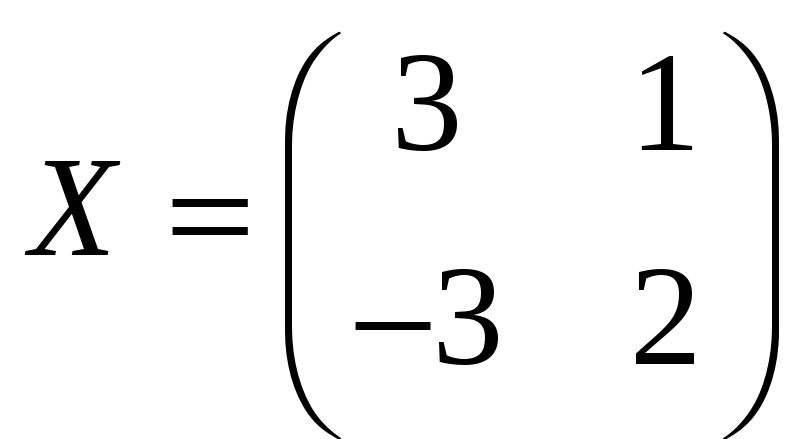 ,
,
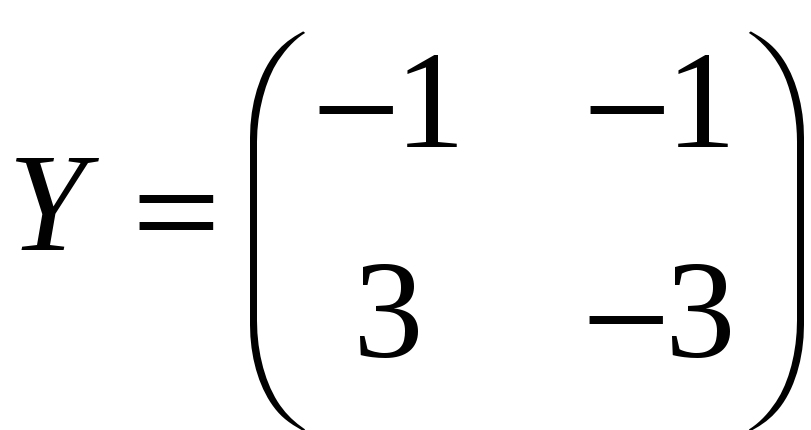 ;
б)
;
б)
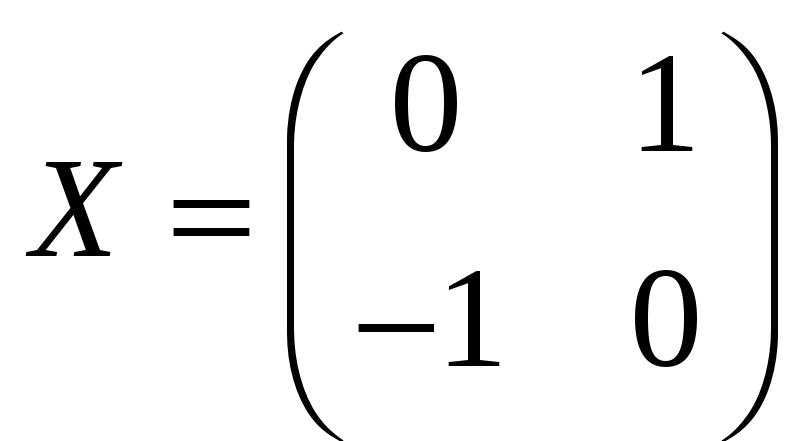 ,
,
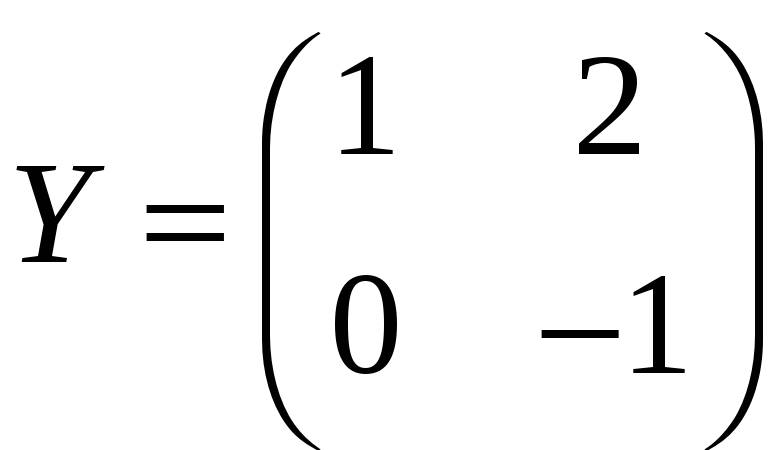 .3.4.
а)
.3.4.
а)
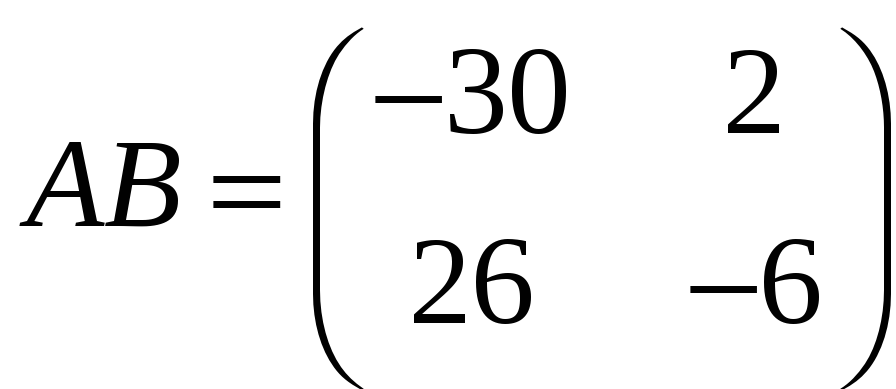 ,
,
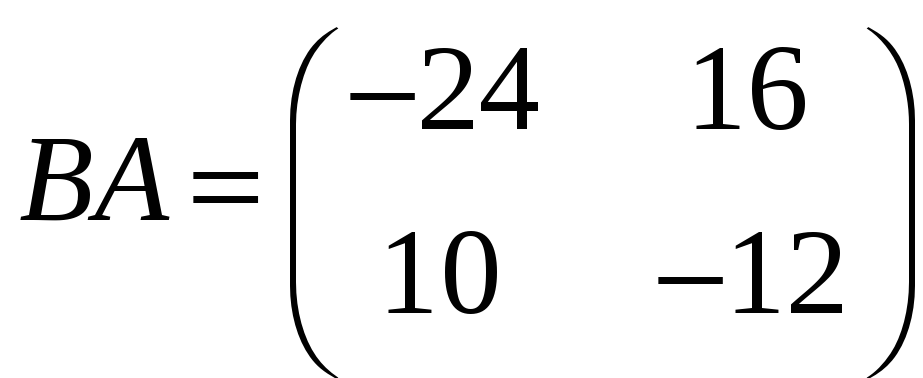 ;
б)
;
б)
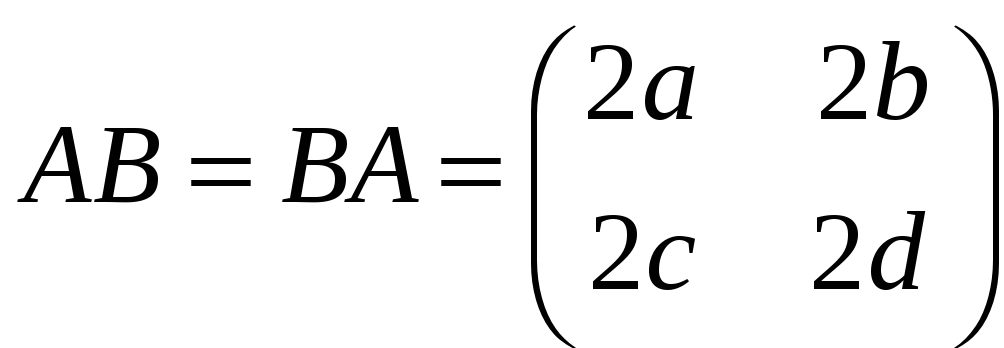 ;
;
в)
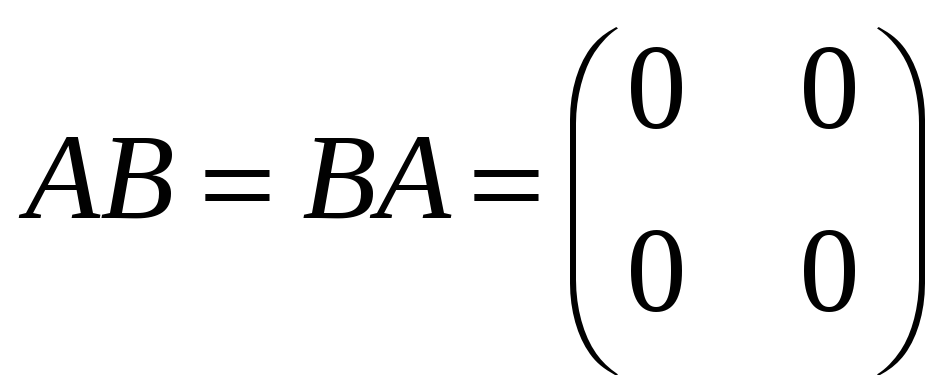 ;
г)
;
г)
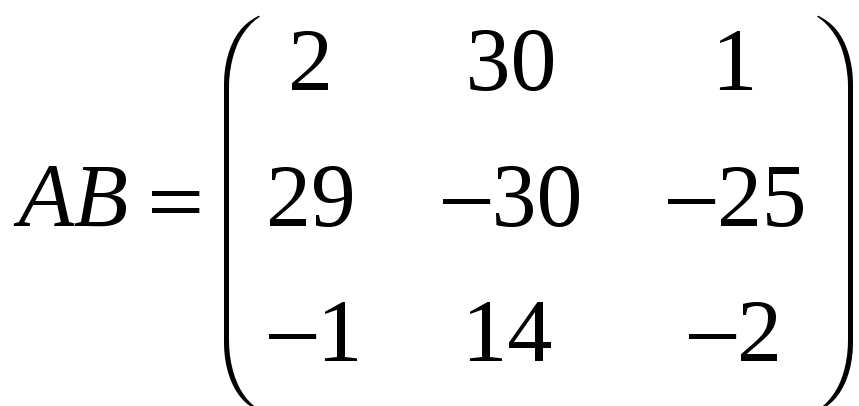 ,
,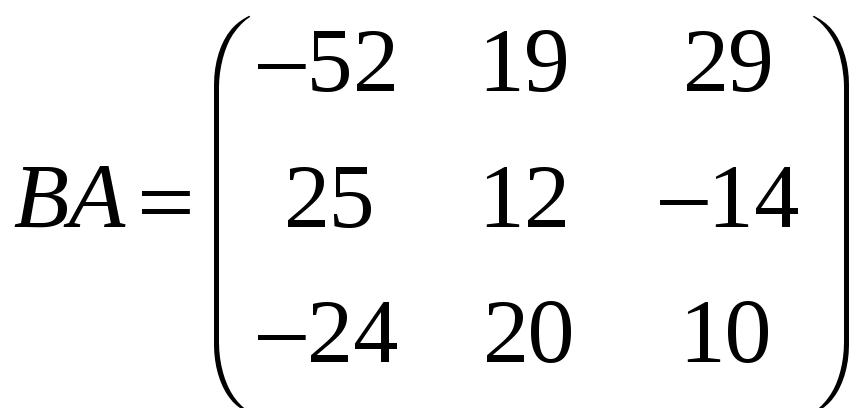 ;
;
д)
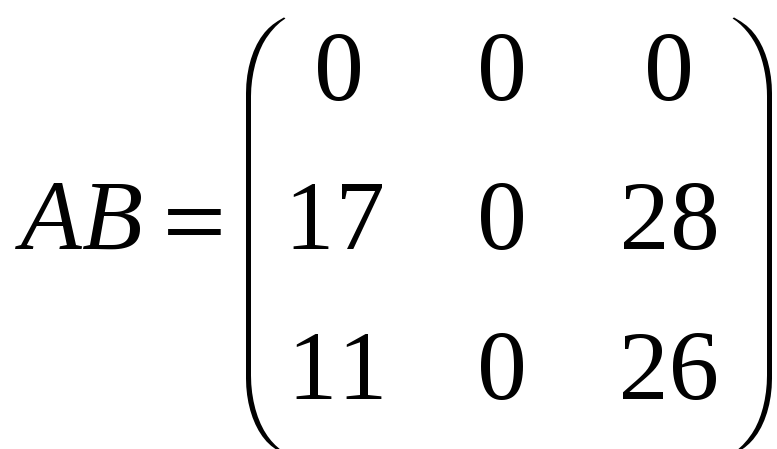 ,
,
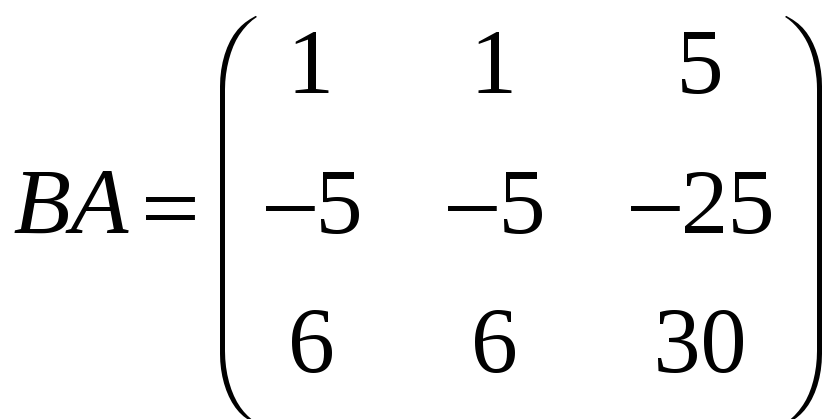 ;
е)
;
е)
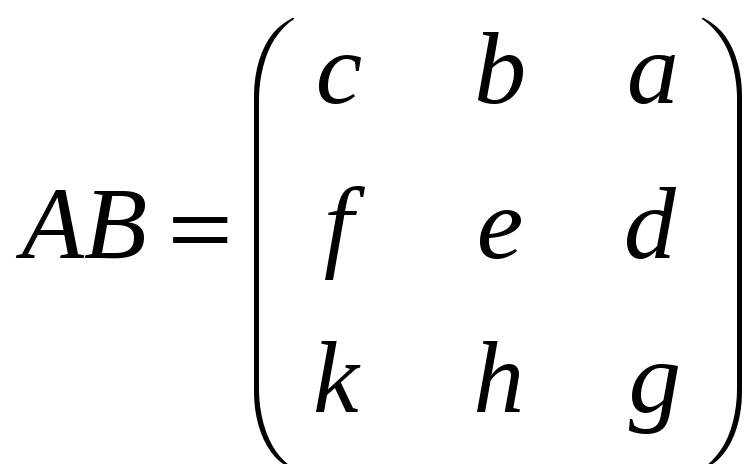 ,
,
 ;
;
є)
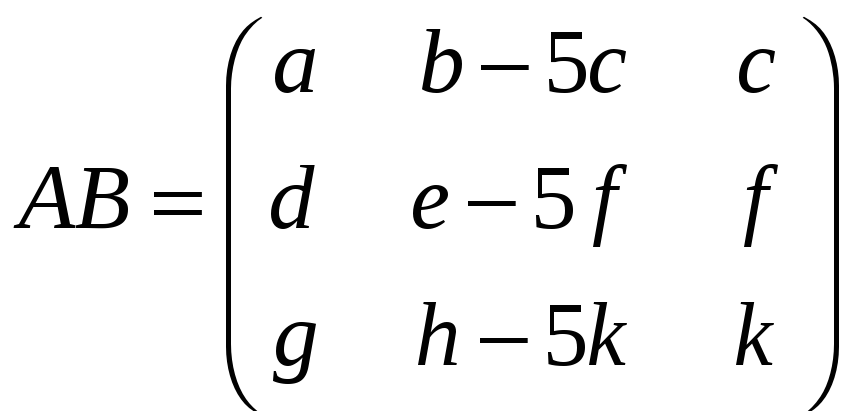 ,
,
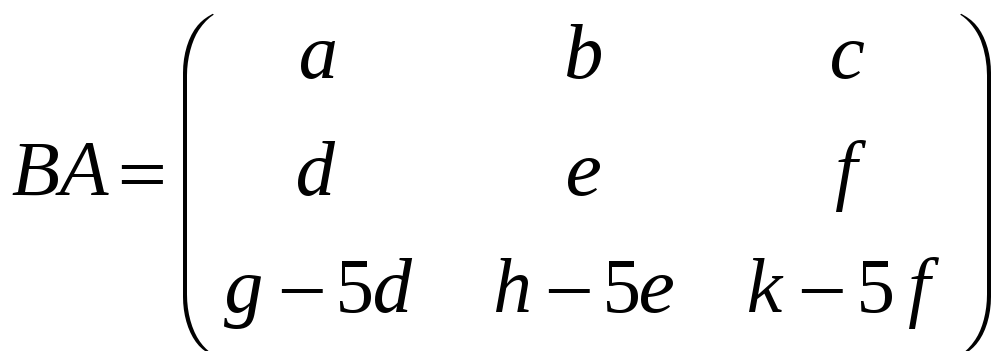 ;
ж)
;
ж)
![]() ;
;
з)
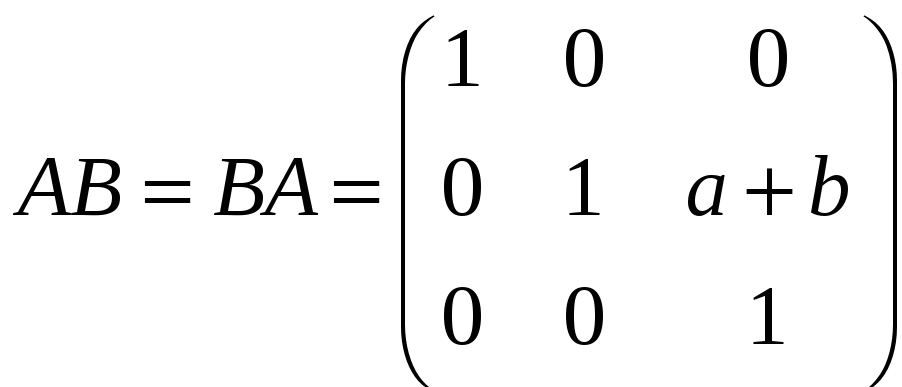 ;
і)
;
і)
 ,
,
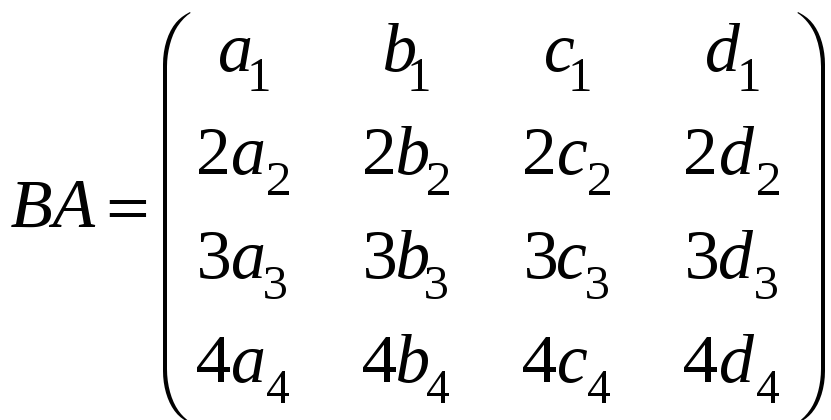 ;
;
к)
 ,
,
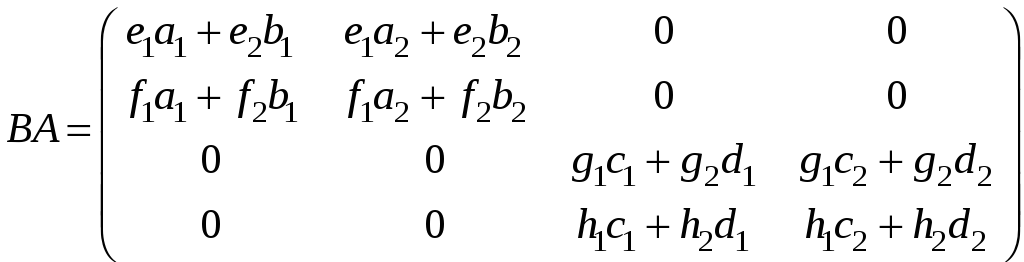 .
3.5.
.
3.5.
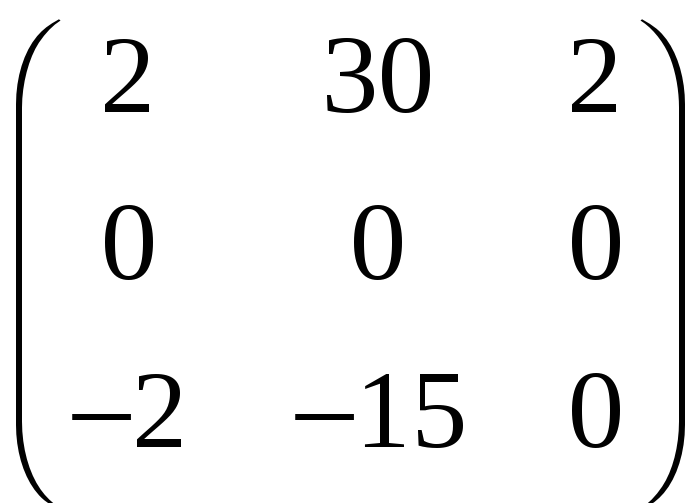 .
.
3.6.
а)
![]() ;
б)
;
б)
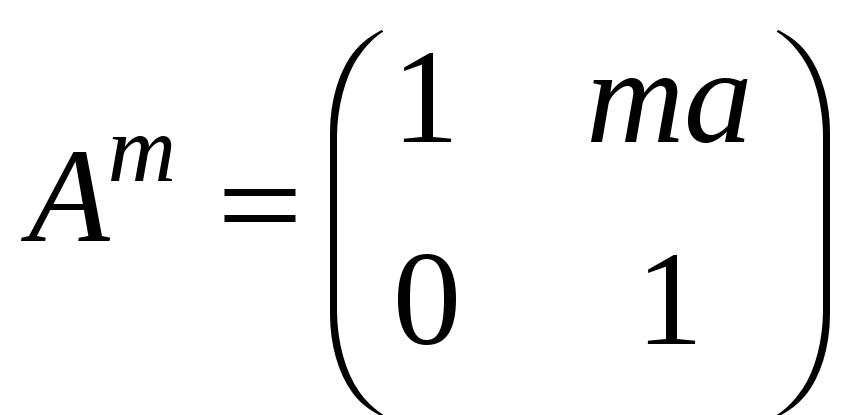 ;
в)
при m
2
;
в)
при m
2
![]() ;
г)
;
г)
![]() ;
;
д)
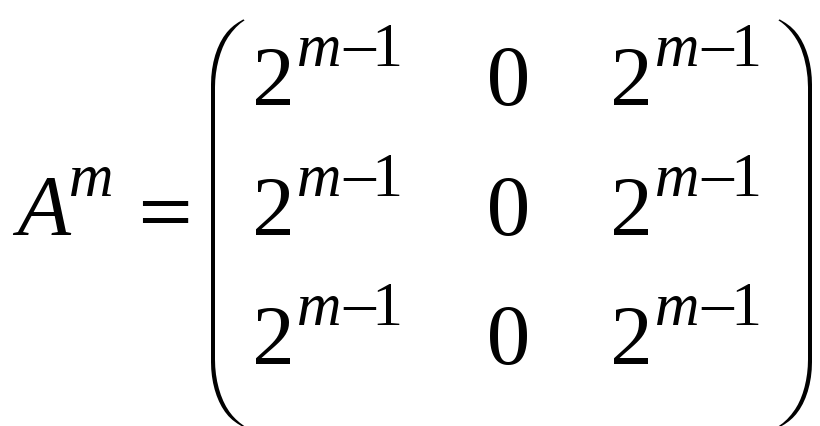 ;
е)
;
е)
![]() ,
якщо m
непарне,
,
якщо m
непарне,
![]() ,
якщо m
парне
;
,
якщо m
парне
;
є)
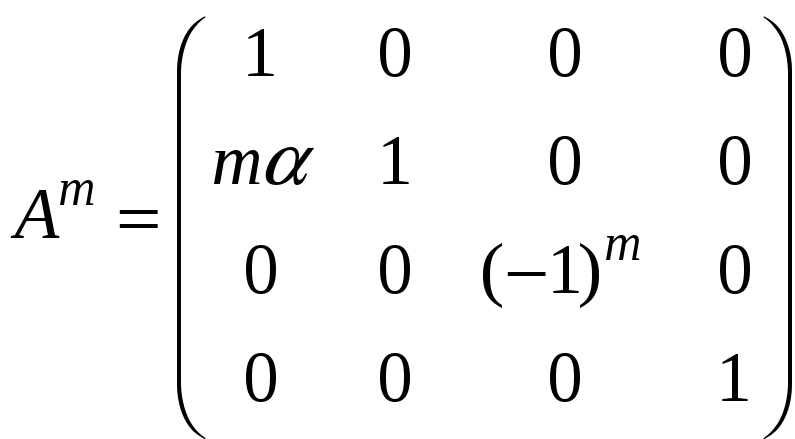 ;
ж)
;
ж)
![]() ;
з)
;
з)
 .
.
3.7.
а)
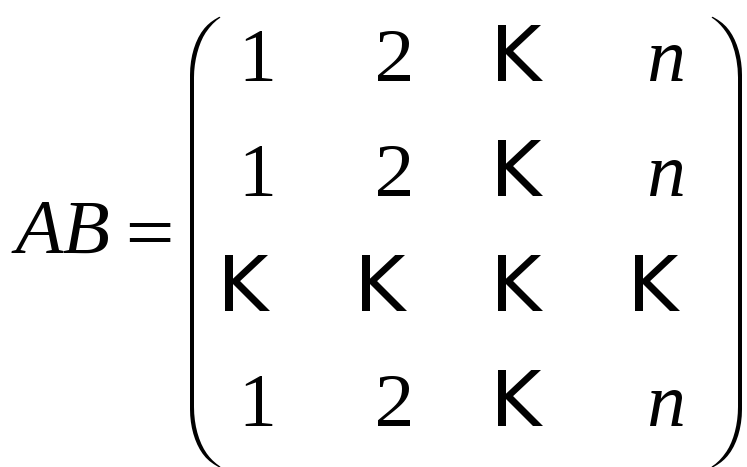 ,
,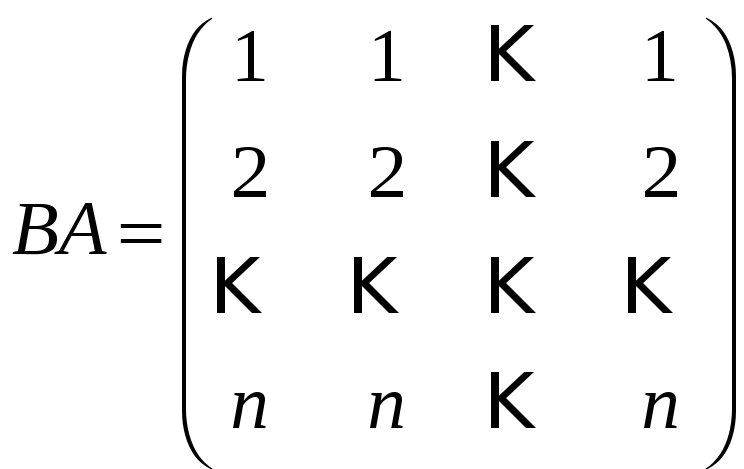 ;
;
б) AB = BA = diag( a1b1, a2b2,, anbn). 3.8. а) E; б) –E. 3.9. а) 34; б) 42; в) 2; г) 4.
3.12.
а)
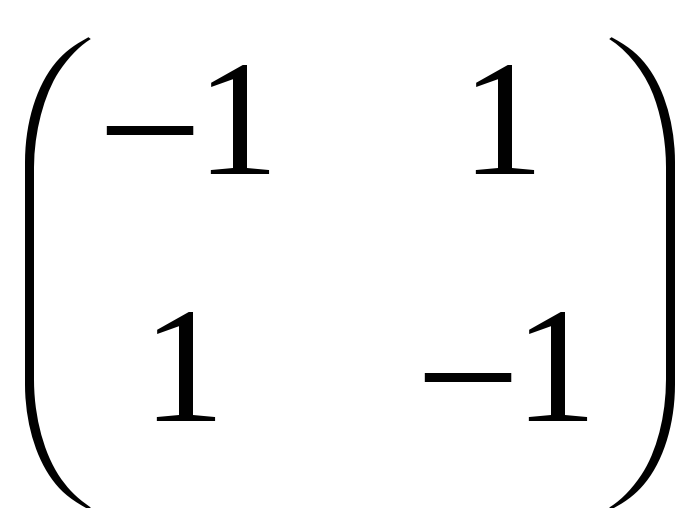 ;
б)
;
б)
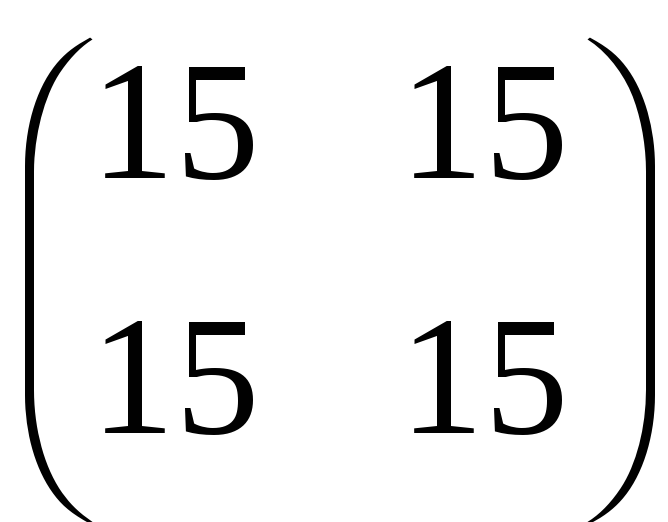 ;
в)
;
в)
 ;
г)
;
г)
 .
.
3.15.
а)
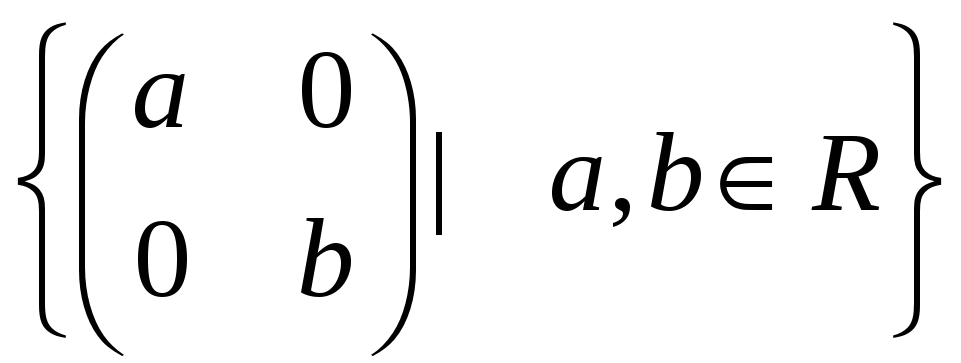 ;
б)
;
б)
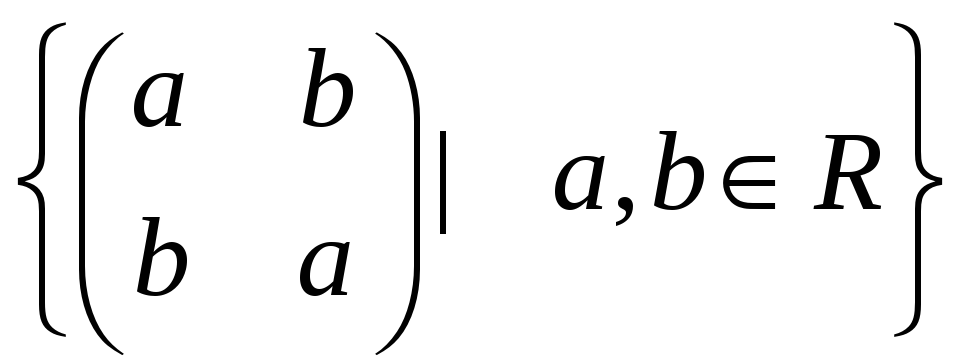 ;
в)
усі квадратні матриці порядку 3; г)
усі діагональні матриці порядку 3; д)
;
в)
усі квадратні матриці порядку 3; г)
усі діагональні матриці порядку 3; д)
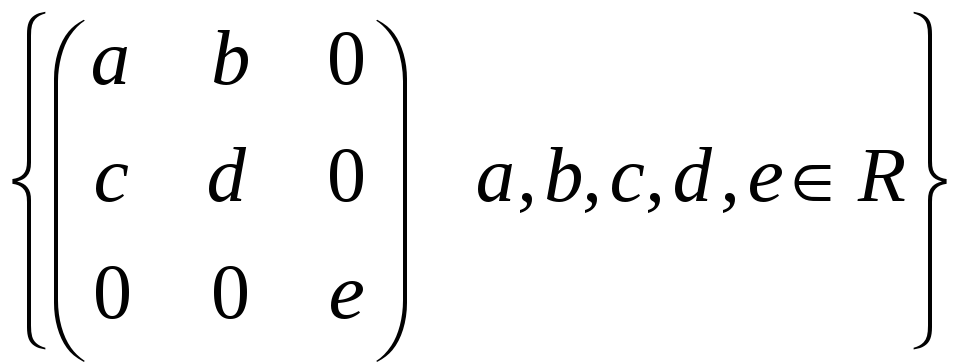 ;
е)
;
е)
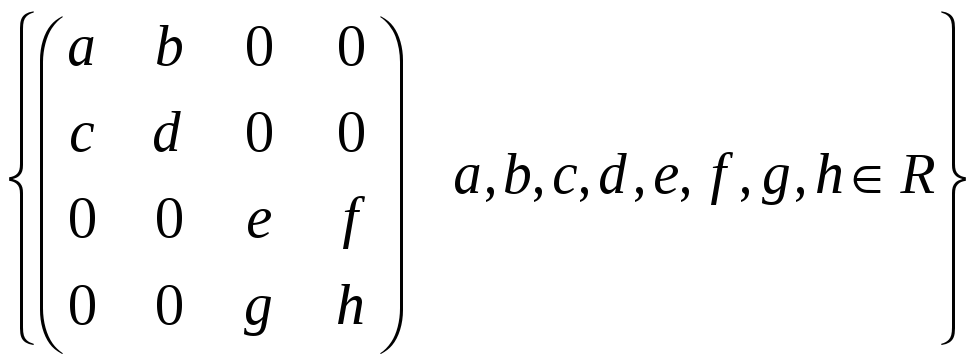 .
3.17.
Усі квадратні матриці порядку n.
.
3.17.
Усі квадратні матриці порядку n.
3.19.
![]() ,
де
,
де

3.20.
![]() ,
де
,
де
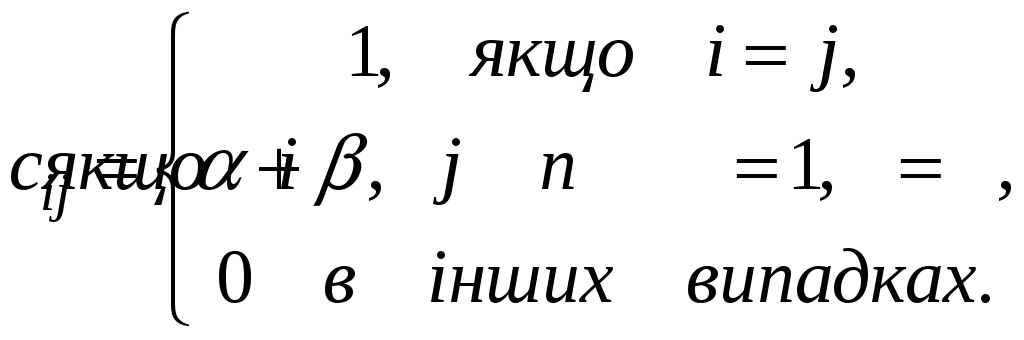 D
= C.
3.21.
n.
D
= C.
3.21.
n.
