Свойства бесконечно больших величин (ббв).

1.Произведение бесконечно большой величины на функцию, предел которой отличен от нуля, есть величина бесконечно большая.

2. Сумма бесконечно большой величины и ограниченной функции есть величина бесконечно большая.

3. Частное от деления бесконечно большой величины на функцию, имеющую предел, есть величина бесконечно большая.

2.6. Бесконечно малые (БМ) функции.

Определение. Функция называетсябесконечно малой при или, если еепредел равен нулю, то есть:

или . (9)

Из определения предела следует, что если ,то это означает, что для любого наперед заданного сколь угодно малого положительного числанайдется положительное число, зависящего от, то есть, такое, что для всехи удовлетворяющих условию

(10)

выполняется неравенство

. (11)

Например. Функция является бесконечно малой при , поскольку

Связь бесконечно малых (бм) с пределами функций.

Теорема. Если функция приилиимеет предел, равный, то ее можно представить в виде суммы этого числаи бесконечно малойприили

(12)

и наоборот,если функция представима в виде соотношения(12),то число есть предел этой функции приили, то есть

. Свойства бесконечно малых (бм) функций.

1.Алгебраическая сумма конечного числа БМ есть функция БМ.

2.Произведение БМ функции на ограниченную функциюприилиесть функция БМ.

3.Если стремится к нулю приилии не обращается в ноль, тостремится к бесконечности.

4.Частное от деления БМ величинына функцию, предел которой отличен от нуля, есть величина БМ.

Сравнение бесконечно малых.

Свойство 4 не рассматривает предел отношения двух бесконечно малых величин и из-за его неопределенности. Этот предел может быть равен нулю, числу, или бесконечности.

Пусть и - БМ при или .

1.Если, где – число, не равное нулю, то говорят, чтои- бесконечно малые одного и того же порядка малости..

В частности, если , тоиназываютсяэквивалентными и пишут~.

2.Если, то это означает, что. То есть,является бесконечно малой более высокого порядка малости, по сравнению с.

3.Еслине существует, то функциииназываютсянесравнимыми.

При вычислении пределов полезно воспользоваться следующим свойством эквивалентных бесконечно малых:

Если отношение двух бесконечно малых имеет предел, то этот предел не изменится при замене каждой из бесконечно малых на эквивалентную ей бесконечно малую, то есть:

.

Приэквивалентны следующие бесконечно малые:

2.7. Основные теоремы о пределах.

1. Если функция имеет предел при, то он единственный.

2. Предел постоянной величины равен самой постоянной:

, где .

3. Предел алгебраической суммы конечного числа функций, имеющих конечные пределы, равен алгебраической сумме пределов этих функций:

.

4. Предел произведения конечного числа функций, имеющих конечные пределы, равен произведению пределов этих функций:

5. Постоянный множитель можно выносить за знак передела:

.

6. Предел частного двух функций равен частному пределов этих двух функций при условии, что эти пределы существуют, и предел делителя отличен от нуля:

7. Предел степени переменной равен той же степени предела основания:

.

8. Если , аи предел, то предел сложной функцииравенА:

.

2.8. Замечательные пределы.

2.8.1. Первый замечательный предел.

Рассмотрим предел .

При вычислении данного предела нельзя воспользоваться теоремой о пределе частного, так как, предел знаменателя равен нулю. Предел числителя также равен нулю, то есть, имеем неопределенность вида. Геометрически доказано, что предел отношения синуса бесконечно малого аргумента к аргументу равен 1:

.

Это соотношение называется первым замечательным пределом.

Отметим, что вместо х в данном соотношении может стоять любая другая бесконечно малая величина.

Например.

1. ,.

2. (прии ).

2.8.2. Второй замечательный предел.

Было установлено, что предел переменной величины при(=1,2,3,… - возрастающая переменная натурального ряда), равен некоторому иррациональному числу, обозначенномуи находящемуся в пределах: . Более точное значение числа

Функция притакже стремится к числу:

.

Это соотношение называется вторым замечательным пределом.

При вычислении этого предела имеем неопределенность вида .

В выражении вместо может стоять и другая бесконечно большая величина. Тогда предел такой функции сводится ко второму замечательному пределу.

Например.

1.

2. .

2.9. Вычисление пределов с помощью свойств бесконечно малых и замечательных пределов.

Непосредственное вычисление пределов.

1. .

2.

По свойству 3 БМ величин: если , то. По свойству 1 ББВ:. Частное от деления ограниченной величины на БМ есть величина бесконечно большая.

3. .

Раскрытие неопределенности вида и.

4. =.

Имеем неопределенность . Выделимкритический множитель, дающий неопределенность. Разложим числитель как разность квадратов, а в знаменателе вынесемх. Критическим множителемявляется, предел которогоравен нулю. На него можно сократить числитель и знаменатель, так как примножитель, оставаясь не равным нулю.

5. . Умножим числитель и знаменатель на выражение, сопряженноечислителю:

.

6. .

Сделаем замену:. Тогда; при.

.

7. 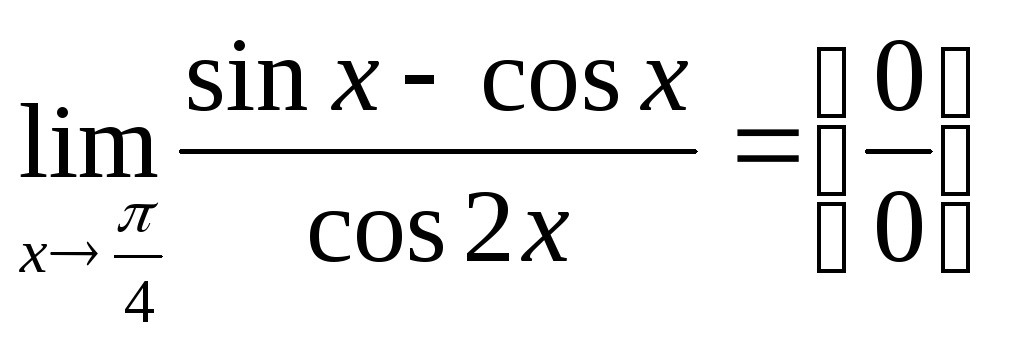.Воспользуемся выражением для косинуса двойного угла.

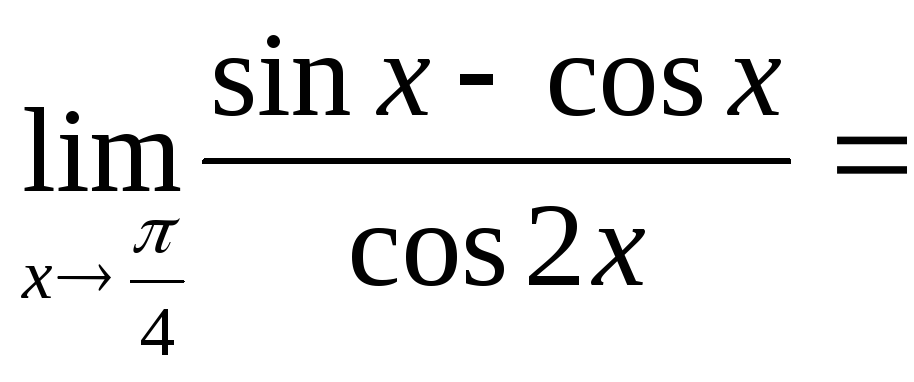
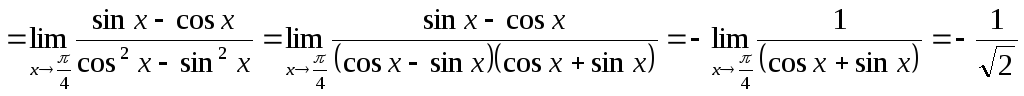
8. .

Разделим числитель и знаменатель на максимальную степеньчислителя и знаменателя:

.

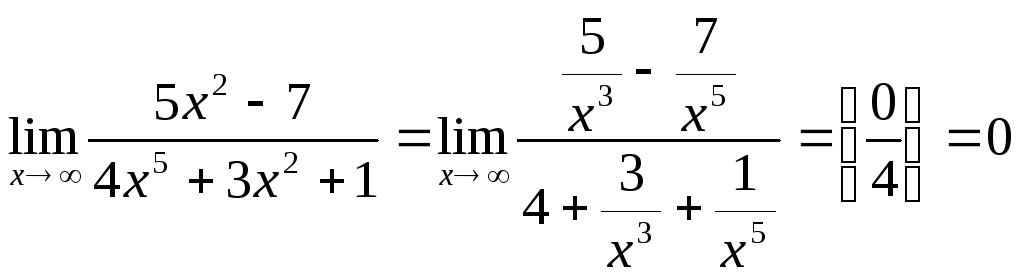То есть, знаменатель – бесконечно большая величина более высокого порядка, чем числитель.

9. .

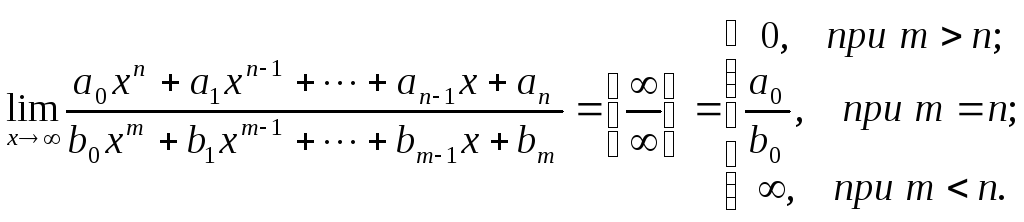Раскрытие неопределенностей вида .

Неопределенности такого вида раскрываются путем преобразования и сведения их к неопределенности вида и .

10. .

Рассмотрим два случая, когда и

а)

Перенесем иррациональность из числителя в знаменатель, умножив на сопряженное выражение.

.

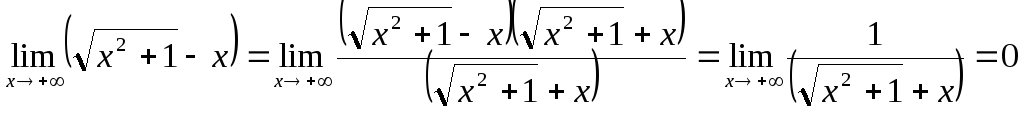б) .

Неопределенности нет. Сумма двух бесконечно больших величин есть величина бесконечно большая.

Использование замечательных пределов.

11. .

Преобразуем числитель, воспользовавшись соотношением между косинусом целого угла и функциями половинного угла:.

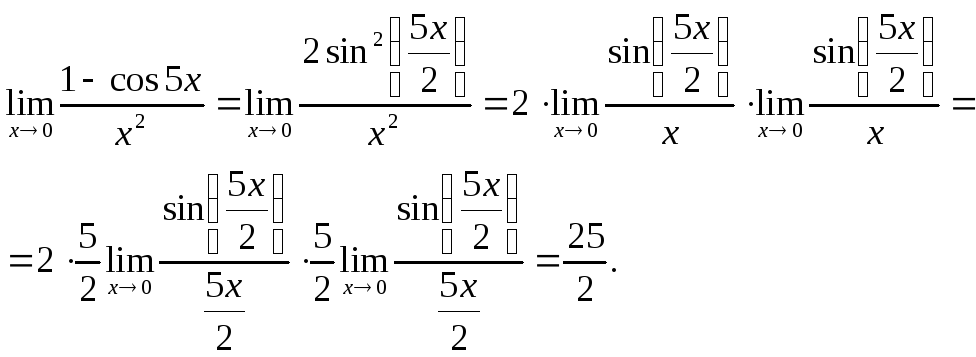
12. .

Заменим эквивалентными бесконечно малыми: при .

13.

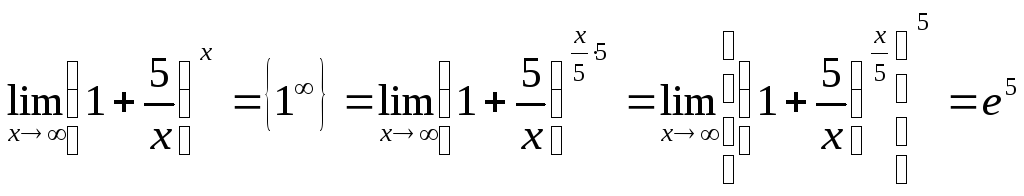
14.