
- •Раздел 1.Введение в математичекий анализ.
- •1. Понятие функции одной переменной
- •Способы задания функций.
- •2. Предел функции.
- •2.1. Предел функции в точке на языке (по Коши).
- •2.2. Односторонние пределы.
- •Классификация точек разрыва.
- •2.5. Бесконечно большие функции.
- •Свойства бесконечно больших величин (ббв).
- •Связь бесконечно малых (бм) с пределами функций.
- •. Свойства бесконечно малых (бм) функций.
- •Сравнение бесконечно малых.
- •2.7. Основные теоремы о пределах.
Раздел 1.Введение в математичекий анализ.
1. Понятие функции одной переменной
Переменной называется величинаx, которая в течение данного процесса принимает различные значения.
Постоянную величину
![]() можно рассматривать как частный
случай переменной, принимающей одно и
то же значение
можно рассматривать как частный
случай переменной, принимающей одно и
то же значение![]() .
.
Совокупность (множество) всех
значений, которые принимает переменная
величина
![]() ,
называетсяобластью изменения
переменной и обозначают
,
называетсяобластью изменения
переменной и обозначают ![]() .
.
Переменная величина
![]() считается заданной, если известно
множество значений
считается заданной, если известно
множество значений![]() ,
которое она принимает.
,
которое она принимает.
Определение. Переменная величина
![]() называетсяфункцией от
переменной
называетсяфункцией от
переменной
![]() если каждому значению переменной
если каждому значению переменной
![]() из области ее изменения
из области ее изменения ![]() ,
то есть,
,
то есть,![]() ,
поставлено в соответствие по
некоторому правилу или закону одно
определенное значение
,
поставлено в соответствие по
некоторому правилу или закону одно
определенное значение
![]() из области изменения
из области изменения![]() ,
то есть,
,
то есть,
![]() (однозначная функция).
(однозначная функция).
Тот факт, что переменная
![]() есть функция от
есть функция от
![]() записывается следующим образом:
записывается следующим образом:![]() .
.
Переменная
![]() называетсянезависимой
переменной или аргументом,
называетсянезависимой
переменной или аргументом,
![]() – зависимая
переменная.
– зависимая
переменная.
Буквами![]() обозначают правило или закон, по которому
аргументу
обозначают правило или закон, по которому
аргументу
![]() ставится в соответствие зависимая
переменная
ставится в соответствие зависимая
переменная
![]() .
.
Область изменения аргумента ![]() называетсяобластью определения
или существования функции,а
множество
называетсяобластью определения
или существования функции,а
множество
![]() –областью изменения функции.
–областью изменения функции.
Геометрически значение переменной изображается точкой на числовой оси - бесконечной прямой, на которой выбрана произвольная точка отсчета0, положительное направление (указывается стрелкой) и масштаб длины.
Область существования
![]() функции
функции![]() может состоять как из отдельных точек
(значений), так и из совокупности точек.
может состоять как из отдельных точек
(значений), так и из совокупности точек.
Если переменная
![]() находится в пределах:
находится в пределах:
1.
![]() - то область
- то область![]() называется отрезокили
замкнутый промежуток
называется отрезокили
замкнутый промежуток![]() .
.
2.
![]() ,
то область
,
то область![]() называется интервал,
открытый промежуток (a,b).
называется интервал,
открытый промежуток (a,b).
3.![]() или
или![]() ,
то область
,
то область![]() называется полуинтервал (a,b],
[a,b)
называется полуинтервал (a,b],
[a,b)
Наряду с этими рассматриваются
бесконечные и полубесконечные интервалы
и полуинтервалы:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
Отрезок, интервал, полуинтервал объединяют общим термином – промежуток.
Если
![]() -
некоторое значение независимой переменной
из области определения функции, то
есть
-
некоторое значение независимой переменной
из области определения функции, то
есть![]() ,
то ему будет соответствовать некоторое
значение
,
то ему будет соответствовать некоторое
значение![]() из
области изменения функции
из
области изменения функции![]() .
Это значение
.
Это значение![]() называютзначением функции в точке
называютзначением функции в точке![]() .
.
Например, если
![]() ,
то
,
то![]() .
.
Способы задания функций.
Существует несколько основных способов задания функций.
1. Табличный способ:
|
х |
|
|
|
|
|
у |
|
|
|
|
2. Графический – изображение графика
функции
![]() .
.
3. Аналитический – когда функция задана одной или несколькими формулами:
![]()
2. Предел функции.
2.1. Предел функции в точке на языке (по Коши).
Пусть функция![]() задана в некоторой окрестности точки
задана в некоторой окрестности точки![]() за
исключением, быть может, самой точки
за
исключением, быть может, самой точки![]() .
Рассмотрим поведение функции при
.
Рассмотрим поведение функции при![]() .
.
Определение. Число А называется
пределом функции ![]() при
при
![]() стремящемся к
стремящемся к![]() (
или в точке
(
или в точке
![]() ),
и пишут
),
и пишут
![]() ,
если для любого сколь угодно малого
положительного числа
,
если для любого сколь угодно малого
положительного числа![]() найдется положительное число
найдется положительное число
![]() ,
зависящего от
,
зависящего от![]() ,
то есть
,
то есть![]() ,
такое, что для всех
,
такое, что для всех![]() и удовлетворяющих условию
и удовлетворяющих условию
![]() (1)
(1)
выполняется неравенство
![]() .
(2)
.
(2)
Геометрический смысл предела функции в точке.
Неравенства (1) и (2) эквивалентны двойным неравенствам:
![]() ,
,
![]() .
.
Интервал (![]() называется
называется
![]() -окрестностью
точки
-окрестностью
точки
![]() ,
а интервал(
,
а интервал(![]() )
-
)
-
![]() -окрестностью
точки А.
-окрестностью
точки А.
Тот факт, что число А является
пределом функции![]() при
при![]() геометрически означает: каков бы ни был
наперед заданный интервал
геометрически означает: каков бы ни был
наперед заданный интервал
![]() ,
лежащий на оси
,
лежащий на оси![]() ,
найдется
,
найдется
![]() -окрестность
точки
-окрестность
точки
![]() (такое
значение числа
(такое
значение числа
![]() ),лежащая на оси
),лежащая на оси![]() ,
такая, что для всех значений аргумента
функциихиз этой окрестности,
исключая, быть может, саму точку
,
такая, что для всех значений аргумента
функциихиз этой окрестности,
исключая, быть может, саму точку
![]() (
(![]() )
,соответствующие значения функции
будут находиться в
)
,соответствующие значения функции
будут находиться в
![]() -окрестности
точкиА. При этом график функции
-окрестности
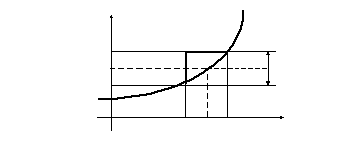
точкиА. При этом график функции![]() будет лежать внутри прямоугольника,
ограниченного прямыми
будет лежать внутри прямоугольника,
ограниченного прямыми![]() (рис.1).
(рис.1).
![]()
![]()

![]()
A
![]()
![]()
О
![]()
![]()
![]()
![]()
Рис.1. Геометрический смысл предела функции в точке
Замечание. Определение
предела не требует, чтобы функция
существовала в самой точке
![]() ,
а только в ее окрестности. То есть,
поведение функции, и предел функции
рассматриваются в окрестности точки и
не связаны со значением функции или
отсутствием значения функции в самой
точке.
,
а только в ее окрестности. То есть,
поведение функции, и предел функции
рассматриваются в окрестности точки и
не связаны со значением функции или
отсутствием значения функции в самой
точке.
Пример. Покажем, что![]() ,
хотя функция
,
хотя функция![]() в точке
в точке
![]() не определена.
не определена.
Пусть задано произвольное число
![]() .По определению, необходимо найти
такое
.По определению, необходимо найти
такое![]() ,
чтобы для всех значений аргументов
функции из
,
чтобы для всех значений аргументов
функции из![]() -окрестности
точки
-окрестности
точки![]() = 3, то есть,
= 3, то есть,![]() , выполнялось неравенство:
, выполнялось неравенство:
![]()
![]() .
.
Разложив в числителе разность квадратов, получим следующие эквивалентные неравенства:
![]() .
.
В самой точке
![]() знаменатель обращается в ноль, однако,
в окрестности точки при
знаменатель обращается в ноль, однако,
в окрестности точки при![]() знаменатель
знаменатель![]() и дробь можно сократить на число, отличное
от нуля.
и дробь можно сократить на число, отличное
от нуля.
![]() .
.
Если взять
![]() ,
то для всех
,
то для всех
![]() ,
из
,
из![]() окрестности
точки
окрестности
точки![]() будет выполняться неравенство
будет выполняться неравенство![]()
![]() .
Значит, предел в точке
.
Значит, предел в точке![]() = 3 равен 6.
= 3 равен 6.
