
Иследование функций с помощью производной
.docxИсследование функций с помощью производных
1. Возрастание и убывание функций
Теорема 1.
Если во всех точках х некоторого
промежутка D производная
функции
 ,
то функция
,
то функция
 постоянна на этом промежутке.
постоянна на этом промежутке.
Доказательство
Функция
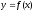 удовлетворяет всем условиям теоремы
Лагранжа, т.е. для любых точек
удовлетворяет всем условиям теоремы
Лагранжа, т.е. для любых точек
 из промежутка D
существует точка
из промежутка D
существует точка
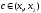 такая, что справедлива формула конечных
приращений Лагранжа:
такая, что справедлива формула конечных
приращений Лагранжа:
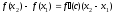 .
По условию теоремы
.
По условию теоремы
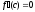 ,
следовательно,
,
следовательно,
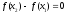 .
Отсюда
.
Отсюда
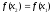 .
Это означает, что функция
.
Это означает, что функция
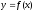 постоянна на этом промежутке, что и
требовалось доказать.
постоянна на этом промежутке, что и
требовалось доказать.
Теорема 2.
Для того чтобы дифференцируемая на
интервале (a, b)
функция
 была возрастающей, необходимо и
достаточно, чтобы выполнялось условие
была возрастающей, необходимо и
достаточно, чтобы выполнялось условие
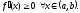 (1)
(1)
Аналогично условие
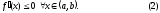
является необходимым и достаточным для
убывания функции
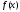 на интервале (a, b).
на интервале (a, b).
Доказательство
Необходимость
Пусть
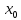 – произвольная точка интервала (a,
b). Из определения
возрастающей функции имеем:
– произвольная точка интервала (a,
b). Из определения
возрастающей функции имеем:
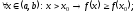

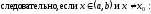
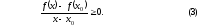

Достаточность
Пусть выполняется условие (1) и
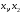 - произвольные точки из промежутка (a,
b), причем
- произвольные точки из промежутка (a,
b), причем
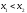 .
Тогда по теореме Лагранжа существует
точка
.
Тогда по теореме Лагранжа существует
точка
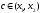 такая, что справедлива формула конечных
приращений Лагранжа:
такая, что справедлива формула конечных
приращений Лагранжа:
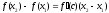 .
.
По условию теоремы
 и
и
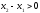 ,
следовательно,
,
следовательно,
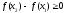 .
Отсюда,
.
Отсюда,
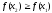 ,
т.е. функция не убывает, что и требовалось
доказать.
,
т.е. функция не убывает, что и требовалось
доказать.
Определение 1. Промежутки возрастания и убывания называются промежутками монотонности.


α
α

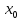
Рис.1 Рис.2
Геометрический смысл: если
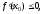 то угол α – тупой (рис.1), если
то угол α – тупой (рис.1), если
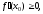 то угол α – острый (рис.2).
то угол α – острый (рис.2).
2. Экстремумы.
пределение 2. Точка, отделяющая промежуток возрастания от промежутка убывания и наоборот, называется точкой экстремума.
Определение 3. Пусть функция
 определена на [a, b].
Точка
определена на [a, b].
Точка
 называется
точкой максимума функции
называется
точкой максимума функции
 ,
если для любого х из некоторой
достаточно малой окрестности точки
,
если для любого х из некоторой
достаточно малой окрестности точки
 выполняется неравенство
выполняется неравенство
 .
Точка
.
Точка
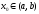 называется
точкой минимума функции
называется
точкой минимума функции
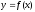 ,
если для любого х из некоторой
достаточно малой окрестности точки
,
если для любого х из некоторой
достаточно малой окрестности точки
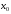 выполняется неравенство
выполняется неравенство
 .
.
Точки максимума и минимума называются точками экстремума.
Теорема 2. (Необходимое условие существования экстремума).
Если функция
 дифференцируема в точке
дифференцируема в точке
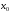 и имеет в этой точке экстремум, то
и имеет в этой точке экстремум, то
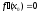 .
.
Точки, в которых производная равна нулю, называются стационарными, а точки, в которых производная равна нулю или терпит разрыв, называются критическими. Все точки экстремума функции находятся среди ее критических точек.
Теорема 3. (Достаточное условие существования экстремума).
Если при переходе через критическую
точку
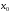 производная меняет знак
производная меняет знак
-
с «+» на «–», то
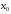 – точка максимума,
– точка максимума, -
с «–» на «+», то
 – точка минимума,
– точка минимума, -
если не меняет знак, то в критической точке экстремума нет.
3. Наибольшее и наименьшее значение функции на отрезке.
1) находят на
 экстремумы;
экстремумы;
2) определяют значения
 на
концах
на
концах
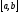 ;
;
3) из всех полученных значений выбирают наибольшее и наименьшее.
Практические задачи: транспортная задача о перевозке груза с минимальными затратами, задача об организации производственного процесса с целью получения максимальной прибыли и другие задачи, связанные с поиском оптимального решения, приводят к развитию и усовершенствованию методов отыскания наибольших и наименьших значений. Решением таких задач занимается особый раздел математики – линейное программирование.
4. Выпуклость и вогнутость.
Пусть функция
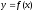 дифференцируема в любой точке интервала
(a, b).
Тогда существует касательная к графику
функции в любой точке графика.
дифференцируема в любой точке интервала
(a, b).
Тогда существует касательная к графику
функции в любой точке графика.
Определение 4. Непрерывная функция
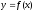 называется выпуклой вниз (т.е.
вогнутой) (рис.3), если все точки кривой
лежат выше любой ее касательной к графику
называется выпуклой вниз (т.е.
вогнутой) (рис.3), если все точки кривой
лежат выше любой ее касательной к графику
 на интервале (a, b).
И называется выпуклой вверх (рис.4),
если все точки кривой лежат ниже этих
касательных.
на интервале (a, b).
И называется выпуклой вверх (рис.4),
если все точки кривой лежат ниже этих
касательных.

Рис.3 Рис.4
Теорема 4.
Если функция
 имеет на интервале (a,
b) конечную вторую
производную
имеет на интервале (a,
b) конечную вторую
производную
 и
и
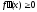 во всех точках х интервала (a,
b), то график данной
функции имеет выпуклость, направленную
вниз (вогнут). Если
во всех точках х интервала (a,
b), то график данной
функции имеет выпуклость, направленную
вниз (вогнут). Если
 во всех точках х интервала (a,
b), то график данной
функции имеет выпуклость, направленную
вверх.
во всех точках х интервала (a,
b), то график данной
функции имеет выпуклость, направленную
вверх.

Определение 5. Точки, при переходе
через которые функция меняет направление
выпуклости, называются точками перегиба
функции
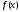 .
.
Определение 6. Точка
 называется точкой перегиба графика
функции
называется точкой перегиба графика
функции
 ,
если существует такая окрестность точки
,
если существует такая окрестность точки
 ,
в пределах которой график функции слева
и справа от точки х0 имеет
разные направления выпуклости.
,
в пределах которой график функции слева
и справа от точки х0 имеет
разные направления выпуклости.
Теорема 5. (необходимое условие существования точки перегиба).
Если функция
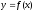 дважды
дифференцируема в точке
дважды
дифференцируема в точке
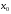 ,
непрерывна в этой точке, и ее график
имеет перегиб в точке
,
непрерывна в этой точке, и ее график
имеет перегиб в точке
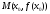 ,
тогда
,
тогда
 .
.
Теорема 6. (достаточное условие существования точки перегиба).
Пусть функция
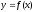 имеет вторую производную
имеет вторую производную
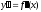 в некоторой окрестности точки
в некоторой окрестности точки
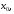 и пусть
и пусть
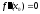 ,
либо
,
либо
 ,
либо
,
либо
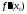 не существует, тогда, если в пределах
указанной окрестности вторая производная
не существует, тогда, если в пределах
указанной окрестности вторая производная
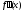 имеет разные знаки слева и справа от
точки х0, то график функции
имеет перегиб в точке
имеет разные знаки слева и справа от
точки х0, то график функции
имеет перегиб в точке
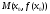 .
.
Замечание. Точка разрыва не является точкой перегиба, хотя при переходе через нее кривая зачастую меняет направление выпуклости.
5. Асимптоты
Определение 7. Прямая
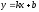 называется асимптотой для кривой
называется асимптотой для кривой
 ,
если расстояние от точки М, лежащей
на кривой, до прямой стремится к нулю
при удалении точки М от начала
координат в бесконечность.
,
если расстояние от точки М, лежащей
на кривой, до прямой стремится к нулю
при удалении точки М от начала
координат в бесконечность.
Существует три вида асимптот: вертикальные, горизонтальные и наклонные.
Определение 8. Прямая
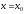 называется вертикальной асимптотой
графика функции
называется вертикальной асимптотой
графика функции
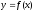 ,
если выполнено хотя бы одно из условий:
,
если выполнено хотя бы одно из условий:


т.е. точка
 является точкой разрыва второго
рода.
является точкой разрыва второго
рода.
Определение 9. Прямая
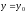 называется горизонтальной асимптотой
графика функции
называется горизонтальной асимптотой
графика функции
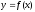 ,
если
,
если
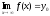 .
.
Определение 10. Прямая
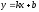 называется наклонной асимптотой
графика функции
называется наклонной асимптотой
графика функции
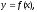 если существуют числа k
и b такие, что
если существуют числа k
и b такие, что
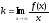 ,
,
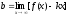 .
.
Замечание. Если оба предела существуют
и конечны (т.е. равны числам), причем
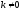 ,
то существует и наклонная асимптота.
Если k = 0, то получим
горизонтальную асимптоту. Если
,
то существует и наклонная асимптота.
Если k = 0, то получим
горизонтальную асимптоту. Если
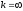 или
или
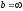 ,
то наклонных асимптот не существует.
,
то наклонных асимптот не существует.
6. План исследования графика функции
-
Найти область определения функции.
-
Найти область непрерывности функции и точки разрыва. Определить характер точек разрыва.
-
Найти нули функции (точки пересечения с координатными осями).
-
Установить, не является ли график функции симметричным относительно какой-нибудь прямой (или координатной оси) или точки, т.е. проверить, является функция четной, или нечетной, или ни той и ни другой.
-
Проверить функцию на периодичность.
-
Найти промежутки монотонности и экстремумы.
-
Найти промежутки выпуклости и точки перегиба.
-
Найти асимптоты.
-
Найти несколько дополнительных значений функции.
-
Построить график.
