Дифференциальные уравнения
.docДифференциальные уравнения
-
Дифференциальные уравнения первого порядка
Дифференциальным уравнением
называется уравнение, связывающее
независимую переменную x,
неизвестную функцию
![]() и ее производные
и ее производные
![]() или дифференциалы.
или дифференциалы.
Замечание: Обязательным в дифференциальном уравнении является только наличие производных или дифференциалов.
Порядком дифференциального уравнения называется порядок высшей производной, в него входящей.
Если дифференциальное уравнение зависит только от одной переменной, то оно называется обыкновенным дифференциальным уравнением.
Обыкновенное дифференциальное уравнение первого порядка имеет вид:
![]() .
(1.1)
.
(1.1)
Если уравнение (1.1) разрешить относительно производной, то его можно записать в виде:
y' (x) = f(x, y(x)). (1.2)
Решением уравнения (1.2) является дифференцируемая функция y(x), которая при подстановке в уравнение (1.2) обращает его в тождество. График решения дифференциального уравнения называется интегральной кривой.
Производную y'(x)
в каждой точке (x,
y) можно геометрически
интерпретировать как тангенс угла![]() наклона
касательной к графику решения, проходящего
через эту точку, т е.
наклона
касательной к графику решения, проходящего
через эту точку, т е.
k = tg![]() = f (x,
y).
= f (x,
y).
Уравнение (1.2) определяет целое семейство решений. Чтобы выделить одно решение, задают начальное условие:
y (![]() )
=
)
=
![]() ,
(1.3)
,
(1.3)
где
![]() –
начальное значение аргумента x,
а
–
начальное значение аргумента x,
а
![]() – начальное значение
функции.
– начальное значение
функции.
Задача Коши заключается
в отыскании функции
![]() ,
удовлетворяющей уравнению (1.2) и начальному
условию (1.3).
,
удовлетворяющей уравнению (1.2) и начальному
условию (1.3).
Общим решением дифференциального
уравнения (1.2) называется решение
![]() этого уравнения, которое:
этого уравнения, которое:
-
зависит от произвольной постоянной с;
-
для всякого начального условия (1.3) можно найти такое значение постоянной
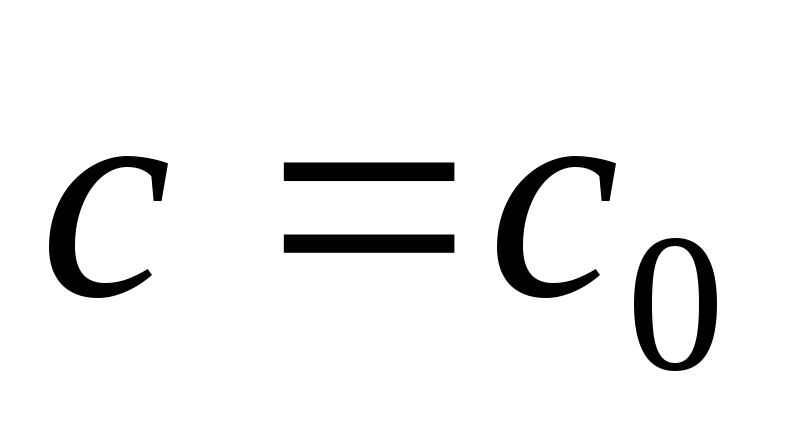 ,
что функция
,
что функция
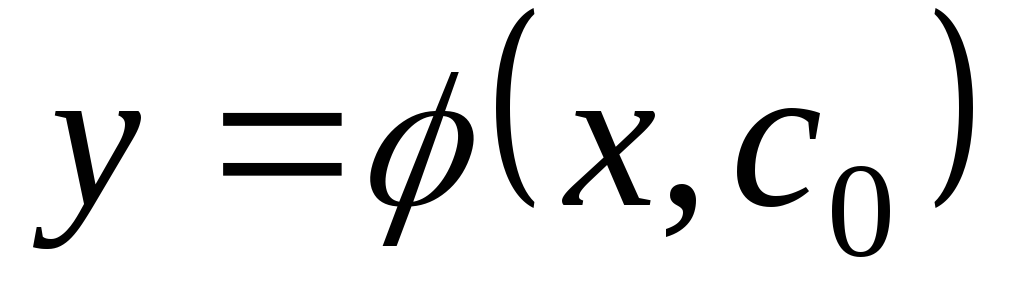 будет удовлетворять данному начальному
условию.
будет удовлетворять данному начальному
условию.
Решение
![]() называется частным решением уравнения
(1.2), соответствующим начальным условиям
(1.3).
называется частным решением уравнения
(1.2), соответствующим начальным условиям
(1.3).
-
Дифференциальные уравнения высших порядков
Дифференциальные уравнения порядка выше первого называются ДУ высших порядков. ДУ второго порядка в общем случае записывается в виде:
![]() (2.1)
(2.1)
или, если это возможно, в виде, разрешенном относительно старшей производной:
![]() .
(2.2)
.
(2.2)
Решением уравнения (2.2) является дифференцируемая функция y(x), которая при подстановке в уравнение (2.2) обращает его в тождество.
Общим решением дифференциального
уравнения (2.2) называется решение
![]() этого уравнения, которое:
этого уравнения, которое:
-
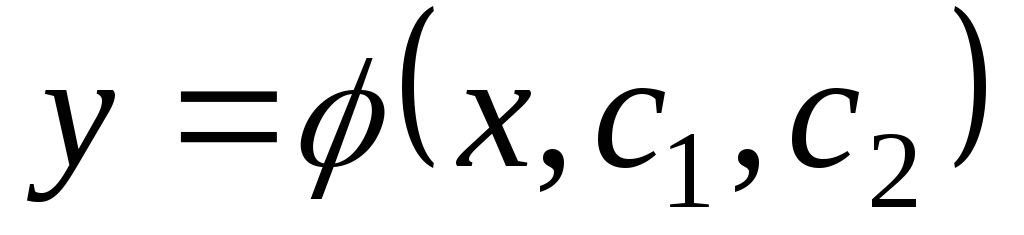 является решением ДУ для фиксированных
значений
является решением ДУ для фиксированных
значений
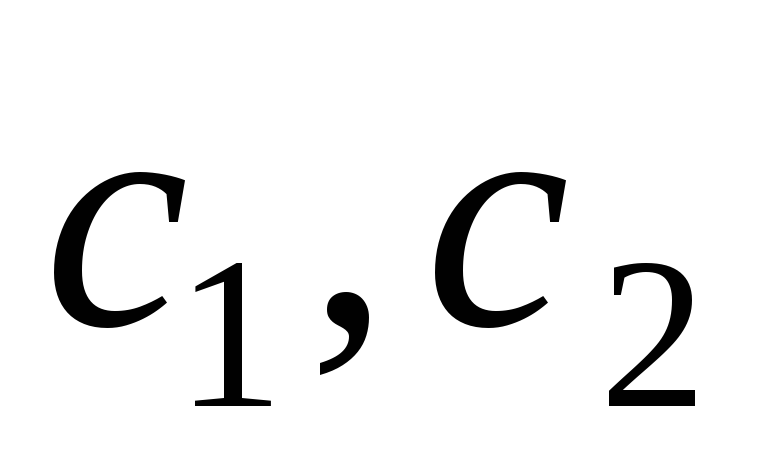 ;
;
-
при заданных начальных условиях
![]() ;
;
![]() (2.3)
(2.3)
можно найти такие значения постоянных
![]() и
и
![]() ,
что функция
,
что функция
![]() будет удовлетворять данным начальном
условиям (2.3).
будет удовлетворять данным начальном
условиям (2.3).
Решение
![]() называется частным решением уравнения
(2.2), соответствующим начальным условиям
(2.3).
называется частным решением уравнения
(2.2), соответствующим начальным условиям
(2.3).
|
Дифференциальные уравнения 1 порядка |
|
|
Вид уравнения |
Решение |
|
Уравнение с разделяющимися переменными
|
|
|
Однородное уравнение
а)
где
б)
в)
где
|
Подстановка:
|
|
Линейное уравнение
где
|
Подстановка:
1)
2)
или:
|
|
Дифференциальные уравнения 2 порядка |
|
|
ЛОДУ с постоянными коэффициентами
|
Характеристическое уравнение:
а)
б)
в)
|