Показники ексцесу.

1. Показник Ліндберга: Е_Х = П – 38,29, де П – це частка варіант, що попадають в інтервал (у відсотках).

2. Показник, заснований на нормованому центральному моменті 4-го порядку: .

Задача № 7. Правило додавання дисперсій

Є наступні дані про робітників однієї із бригад:

Тарифний розряд	Число робітників	Денне виробництво деталей одним робітником, шт.
3 4 5	2 4 5	100, 120 120, 120, 140, 160 140, 160, 170, 180, 200

Визначте за цими даними:

а) внутрішньогрупову дисперсію з виробництва деталей одним робітником, що має даний розряд;

б) середню із внутрішньогрупових дисперсій за трьома групами робітників;

в) міжгрупову дисперсію;

г) загальну дисперсію виробництва деталей робітників цієї бригади.

Методичні рекомендації

Правило додавання дисперсій записується у вигляді рівняння:

, (9)

де – загальна дисперсія; –міжгрупова дисперсія; – середня з групових дисперсій.

Міжгрупова дисперсія характеризує варіацію ознаки у за рахунок фактора х, покладеного в основу групування, і розраховується за формулою:

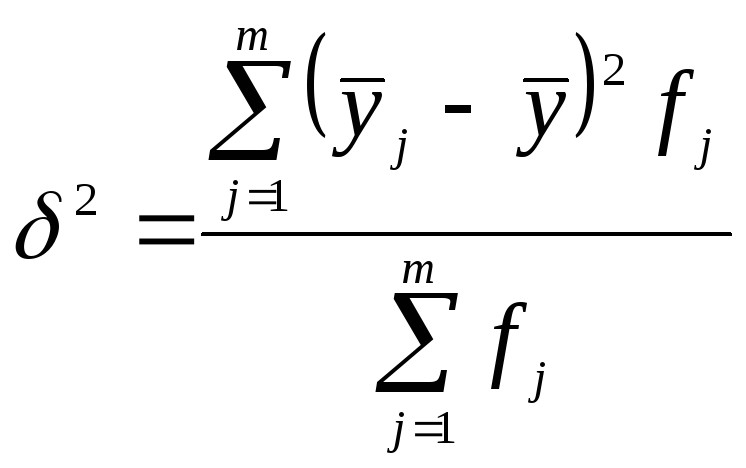, (10)

де , – відповідно середня j-ї групи та загальна середня варіюючої ознаки; f_j – чисельність одиниць (частота) j-ї групи; m – кількість груп.

Внутрішньогрупова дисперсія характеризує варіацію результативної ознаки за рахунок інших факторів, не врахованих у групуванні:

. (11)

Для всіх груп в цілому розраховується середня з групових дисперсій:

. (12)

Задача № 8. Правило додавання дисперсій для частки

Визначте групові дисперсії, середню із групових, міжгрупову й загальну дисперсію частки за даними, що характеризує чисельність студентів всіх форм навчання й питому вагу випускників очної форми навчання, що отримали дипломи з відзнакою за вузами міста.

Вуз	Чисельність студентів всіх форм навчання, чол.	Питома вага випускників очної форми навчання, що одержала дипломи з відзнакою, %
1 2 3 4	1500 3250 2140 1150	13 35 25 12
Разом	8040	–

Методичні рекомендації Правило додавання дисперсій для частки має вигляд:

, (13)

де – загальна дисперсія;– середнє значення частки;– середня із групових дисперсій;– внутрішньогрупові дисперсії;– міжгрупова дисперсія.

Задача № 9. Визначення помилки вибіркової середньої при випадковому безповторному відборі

Нехай є 10 %-на безповторна вибірка виробничих фірм району (табл.1). Необхідно визначити з імовірністю 0,954 середню вартість їхньої товарної продукції.

Таблиця 2 - Вибіркові дані про товарну продукцію фірм

Xi, млн. грн.	fi, фірм
до 3	5
3-5	15
5-10	24
10-30	40
30 і більше	16
Разом	100

Методичні рекомендації

1. Визначимо середню вибіркову вартість товарної продукції:

= X_Іf_i / f_i (14)

2. Визначимо вибіркову дисперсію:

s²=  (Х_І –)²/ f_i (15)

3. Обчислимо середню квадратичну помилку безповторної вибірки (, тому що обсяг вибірки 100>30):

(16)

Задача № 10. Визначення помилки вибіркової частки при випадковому безповторному відборі

За вихідними даними задачі № 9 визначити частку фірм у районі з товарною продукцією до 10 млн. грн.