_02Л_Законы АЛ

Основные законы булевой алгебры

В алгебре логики аналогично обычной математике раскрытие сложных выражений подчиняется определённым законам. Сложные логические выражения выполняются в следующей последовательности:

1)инверсия;

2. конъюнкция;

3. дизъюнкция.

Если необходимо изменить последовательность операций, то используются скобки. Операции в скобках выполняются в первую очередь. Если одни скобки вложены в другие, то вначале выполняются операции во внутренних скобках.

Над логическими выражениями производят тождественные преобразования с использованием законов булевой алгебры.

Две функции являются эквивалентными, если они принимают одинаковые значения на одних и тех же наборах входных переменных.

Две эквивалентные функции, приравненные друг к другу, называются тождеством.

1. Переместительный закон (аналогично обычной алгебре):

—для дизъюнкции

—для конъюнкции

От перемены мест логических слагаемых (сомножителей) их логическая сумма (логическое произведение) не меняется.

2. Сочетательный закон (аналогично обычной алгебре):

—для дизъюнкции

—для конъюнкции

Можно различным образом группировать логические переменные при выполнении операции конъюнкции (дизъюнкции) при этом значение булевой переключательной функции не изменяется.

3. Распределительный закон

Распределительный закон здесь также справедлив, как и в обычной алгебре. Специфика его в булевой алгебре проявляется в некоторых частных случаях. Эти специфичные случаи и формулируются как распределительный закон булевой алгебры:

—для конъюнкции

конъюнкция переменной и дизъюнкции эквивалентна дизъюнкции конъюнкций;

—для дизъюнкции

(a v b)(a v c)=a v bc,

дизъюнкция переменной и конъюнкции равносильна конъюнкции дизъюнкций этой переменной с сомножителями.

Справедливость распределительного закона для дизъюнкции докажем следующими простейшими преобразованиями:

(a v b)(a v c)= (aa v ac v ab v bc)=a v a(b v c) v bc=a(1 v (b v c)) v bc .

В результате получаем

(a v b)(a v c)=a v bc,

так как 1 v (b v c)=1 независимо от выражения в скобках.

4. Закон инверсии. Закон де Моргана.

—для дизъюнкции

отрицание дизъюнкции логических переменных эквивалентно конъюнкции отрицаний этих переменных;

—для конъюнкции

отрицание конъюнкции переменных эквивалентно дизъюнкции отрицаний этих переменных.

Справедливость законов отрицания (де Моргана) докажем с помощью таблиц истинности.

Таблица. Закон отрицания (де Моргана) для дизъюнкции

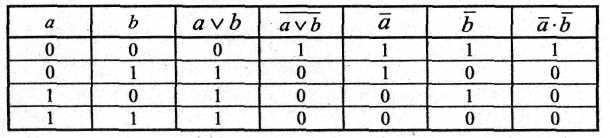
Таблица. Закон отрицания (де Моргана) для конъюнкции

Таблицы 1.5; 1.6 показывают, что на одинаковых наборах переменных значения функций совпадает. Законы де Моргана доказаны.

5. Законы повторения

— для дизъюнкции.

—для конъюнкции

Многократное логическое сложение (логическое умножение) одной переменной равно самой этой переменной.

Законы повторения булевой алгебры существенно отличаются от законов повторения обычной алгебры.

6. Закон двойного отрицания

Двойное отрицание логической переменной равно самой логической перемененной.

7. Соотношения с нулем и единицей

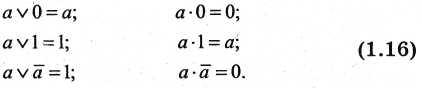
8. Закон склеивания:

Докажем законы склеивания эквивалентными преобразованиями

9. Законы поглощения

Доказательства законов поглощения

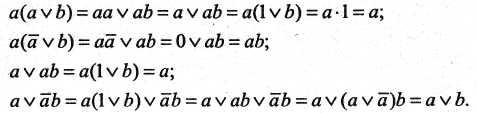
10. Умножение и сложение переменной и функции

Формулы умножения и сложения позволяют существенно упростить техническую реализацию логического устройства, заменить переменную некоторой константой: логической 1 либо логическим 0.

Пример.

Правила алгебры логики позволяют преобразовать логическую функцию к виду, удобному для реализации в виде логического устройства.

Например, задана функция

Для реализации функции в данном виде требуется два инвертора НЕ, три трехвходовых элемента ЗИ, один трехвходовый элемент ЗИЛИ (рис. 3).

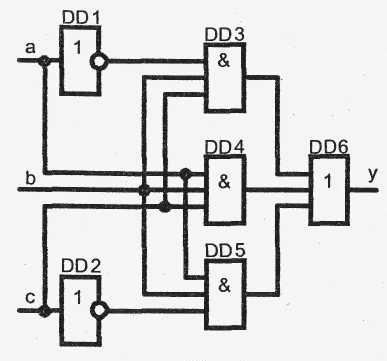
Проведем эквивалентные преобразования с использованием закона поглощения

Очевидно, что после преобразования функция значительно упростилась. Для реализации теперь достаточно иметь один двухвходовый элемент 2И, один двухвходовый элемент 2ИЛИ (рис.3). Обе схемы позволяют реализовать одну и ту же функцию.