46. Прием с перестройкой рабочей частоты(ппрч)

При реализации демодулятора сложного сигнала возникает проблема разработки УПЧ с широким рабочим диапазоном частот. К тому же если каналов много, то создание такого демодулятора весьма сложно. Поэтому делают так, чтобы частота канала менялась во времени, т. е. Передатчик и приемник меняли свои рабочие частоты.

МОД – модулятор

У – усилитель

СМ – смеситель

Атт – аттенюатор

УУ – управляющее устройство

При передачи каждого элементарного сигнала устанавливается соответствующая частота несущей передатчика и частота гетеродина приемника. Полученная последовательность радиоимпульсов попадает на управляемый аттенюатор. Для каждого элементарного импульса анализируется С/Ш и если оно плохое, то посылка «давится» аттенюатором. Полоса пропускания УПЧ определяется полосой частот элементарного сигнала. Вышеописанный ППРЧ не имеет обратной связи с передатчиком её называется ППРЧ с быстрой перестройкой.

Если , то такой ППРЧ называется с медленной перестройкой, у него имеется обратная связь с передатчиком по специальному служебному каналу для синхронизации выбора рабочей частоты.

Пропускная способность канала связи

Чем шире полоса пропускания, тем быстрее могут идти посылки. Если С/Ш большой, то можно повысить скорость канала за счет многоуровневой модуляции. Вероятность ошибки тем больше, чем ниже С/Ш и тем ниже, чем больше расстояние между точками сигнального созвездия, т.е. При увеличении количества уровней (точек сигн. созв-я), тем вероятность ошибки больше. Шеннон вывел формулу, которая определяет максимально возможную пропускную способность канала для данной полосы пропускания:

• ф-ла Шеннона для непрерывного канала.

Для дискретного канала ф-ла Шеннона имеет вид:

V– скорость следования имп-ов;

P– вероятность ошибки.

ЕСЛИ Р=0.5, тоС=0 !!!!!!

Формулы Шеннона не говорят о виде модуляции, они лишь определяют максимальную пропускную способность, которой нельзя достичь к ней можно только стремиться.

47. Подавление замираний с помощью пространственно-разнесенного приема

Е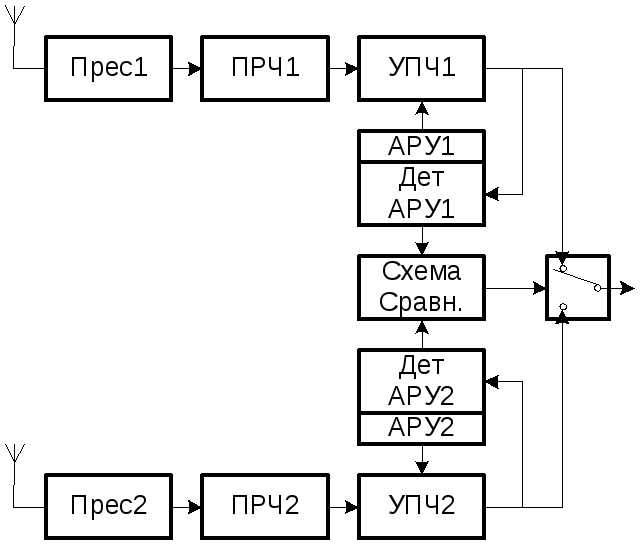сли антенн поставить несколько и разнести их в пространстве, то замирание сигнала происходит не одновременно, если принятые сигналы комбинировать, то можно компенсировать замирания, к тому же можно повысить С/Ш. С/Ш будет максимальным, если каждый сигнал с антенны взвешивать с к-том передачи в данном канале связи. Т.к. С/Ш определить сложно, то используют субоптимальные системы. Самая простая – схемаавтовыбора:

Эта схема не обеспечивает увеличения С/Ш, в отличие от оптимальной схемы. Значительно лучшесхема линейного сложения:

Как видно сигнал с первой антенны с помощью ФАПЧ фазируется с сигналом второй антенны, а за тем сигналы складываются. Чем больше антенн, тем качественней система подавления замираний, тем выше С/Ш, но и тем сложнее система. Обычно антенн до 16 шт. Существуют еще частотное и поляризационное разнесение.

48.Адаптивная компенсация помех.

Если амплитудно-фазовое соотношение по помеховому компоненту на выходах различных антенн различаются от аналогичных соотношений по сигнальному компоненту, то складывая с определенными весами выходные сигналы антенн можно обеспечить подавление помехового компонента.

Рассмотрим простейшую ситуацию когда одна из антенн направлена точно на источник помехи, а другая на источник сигнала, однако по боковым лепесткам принимает помеху.

n₀(jω)= n_ип(jω)k₀(jω)

n₁(jω)= n_ип(jω)k₁(jω)

n₀(jω)-y(jω)=0

y(jω)=k_ф(jω)·n₁(jω)

Характеристики k₀(jω) и k₁(jω) описывают частотные характеристики трактов распространения помехи от источника помехи до А₀ и от источника помехи до А₁. Определим частотную характеристику адаптивного фильтра при которой на выходе вычитающего устройства происходит полное взаимное компенсация помех.

n_ип(jω)k₀(jω)-n_ип(jω) k₁(jω) k_ф(jω)=0

k_ф(jω)=

Эта система может подавлять любую помеху.(внеполосные и внутренние помехи)

Из полученного положения следует, что компенсация происходит независимо от формы помехи. Т.к. заранее характеристики k₀ и k₁ неизвестны и меняются во времени, то фильтр компенсатора помех должен быть адаптивным, и при его разработке решается задача выбора работы фильтра. Если фильтрацию обеспечивать по критерию минимума дисперсии выхода сигнала, то при этом обеспечивается наиболее глубокое подавление помехи.

Обозначим вых. Сигнал через Σ Σ=S +-y

Дисперсия(усреднение по времени) D_Σ=²=²+²+=²+

=0 за счет некоррелированности процессов S-сигнала и n-помехи;

Из этого следует, что минимум D_Σ достигается лишь при обеспечении min 2-ого слагаемого, что означает максимальную взаимную компенсацию процессов n₀ и y.

Рассмотрим простейшую реализацию адаптивного фильтра, когда он представляет собой звено с переменным коэффициентом передачи. Определим оптимальное значение коэффициента передачи, который обеспечивает минимум дисперсии сигнала на выходе.

Σ=S +-ωn ω - коэффициент передачи фильтра;

D_Σ=²=²+²

=0 =ω_опт² ω_опт==**

=ρ

Оптимальные значения коэффициента передачи фильтра определяется степенью коррелированности процесса n₀ n_1, а также отношением их среднеквадратических значений. Определим степень подавления помехи при использовании данного адаптивного фильтра.

D_Σ=(S+-ω_опт)²=-²-2ω_опт+ω_опт² =+²-2+=

=+²-=+²(1-)

D_Σ= +²(1-g)

Если процессы ижестко коррелированны, то ρ=0, при этом обеспечивается полное подавление помехи. Если же эти процессы некоррелированы, то подавление помехи отсутствует.