Лекция 5

многомерное распределение дискретных

и непрерывных случайных величин

5.1. Параметры многомерных распределений [6]

5.2. Двумерное нормальное распределение

Плотность распределения задается выражением [4]:

р_XY(x,y)={1/(2πσ_Xσ_Y√(1-ρ_XY²)}e^-1/2*Q(x,y), (1)

где Q(x,y) =1/(1-ρ_XY²){(x-m_X)²/σ_X²+ (y-m_Y)²/σ_Y²-2 ρ_XY(x-m_X)/ σ_X(y-m_Y)/ σ_Y}

здесь m_x и m_y – центры распределения случайных величин X и Y,

σ_х и σ_у- стандартные отклонения случайных величин X и Y.

Выражение (1) является плотностью двумерного распределения двух линейно коррелированных величин X и Y, каждая из которых в отдельности нормально распределена с соответствующими значениями центра и дисперсии.

Если величины X и Y независимы и нормально распределены с плотностями соответственно N(x, m_x, σ_x) и N(y, m_y, σ_y), то плотность их совместного распределения получается из (1) при ρ_XY=0 как произведение плотностей N(x, m_x, σ_x) и N(y, m_y, σ_y) их одномерных распределений:

Ψ_XY(x,y)={1/(2πσ_Xσ_Y}exp{-1/2*[(x-m_X)²/σ_X²+ (y-m_Y)²/σ_Y² ]}

(2)

Из этого следует, если нормально распределенные величины не 60еаллированны, то они вместе с тем и независимы. Этот вывод не подходит для произвольного закона распределения, а только для нормального.

Рассмотрим условное нормальное распределение, его плотность равна:

р(y/x)={1/(2πσ_Y√(1-ρ_XY²)}exp{-1/2[((y-m_Y)- ρ_XY (σ_Y/σ_X)

(x-m_X))/( σ_Y√(1-ρ_XY²))]²} (3)

Плотность условного распределения Y при данном значении х является нормальным распределением с центром:

M(Y/x)=m_Y/x=m_Y+ ρ_XY (σ_Y/σ_X)(x-m_X), (4)

который является математическим ожиданием Y при данном х

M(Y/x)=m_Y/x . (5)

Точно также условное стандартное отклонение будет:

σ_Y/x=σ_Y√(1-ρ_XY²) (6)

Уравнение (4) представляет вместе с тем уравнение линии нормальной регрессии Y по X, которая является прямой линией.

Аналогично регрессия Х по Y будет также линией, а условная дисперсия равна:

σ_X/y=σ_X²((1-ρ_XY²) (7)

Величина (6) представляет теоретическое среднее квадратическое отклонение погрешностей оценки ожидаемого значения Y по х. Отсюда следует, что оценка Y по х с помощью линии регрессии одинакова при всех значениях х.

Функция плотности вероятности двумерного распределния может быть наглядно отображена в трехмерной плоскости.

y- m_Y= ρ_XY(x-m_X)

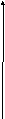
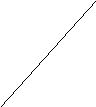
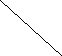
m_Y

m_X

Рисунок 1. Сечение плотности двумерного нормального распределения.

Рассекая поверхность нормального распределения плоскостью, параллельной поверхности х-у, в сечении получаем эллипс, за исключением вырожденного случая ρ_XY=±1. Сечения в разных плоскостях будут давать эллипсы различных размеров с одинаковой ориентацией их главных осей, составляющих некоторый угол с осями координат. Главные оси не могут быть параллельными линии регрессии.

Если значения X, Y не коррелированны, ρ_XY=0, то в сечении будем иметь эллипс с центром m_X, m_y и с главными осями, параллельными осям координат х и у.

Таким образом, с уменьшением силы корреляционной связи между величинами X и Y происходит все больший поворот главных осей эллипсов относительно координатных осей.