2.3. Биномиальное распределение (распределение Бернулли)

Возникает в тех случаях, когда ставится вопрос: сколько раз происходит некоторое событие в серии из определенного числа независимых наблюдений (опытов), выполняемых в одинаковых условиях. Биномиальное распределение названо по имени создателя, швейцарского математика Якоба Бернулли (1654-1705), и является одним из важнейших в математической статистике.

Для удобства и наглядности будем полагать, что нам известна величина p – вероятность того, что событие произошло (наступило) и (1– p) = q – вероятность того, что событие не произошло (не наступило). При этом распределении разброс вариант (произошло или нет событие) является следствием влияния ряда независимых и случайных факторов.

Если X – случайная величина из общего числа n независимых опытов (испытаний), то вероятность того, что среди n исходов оказалось k благоприятных событию равна

, где k=0,1,…n (1)

Формулу (1) называют формулой Бернулли. При большом числе испытаний биномиальное распределение стремиться к нормальному.

2.4. Распределение Пуассона

Играет важную роль в ряде вопросов физики, теории связи, теории надежности, теории массового обслуживания, всюду, где в течение определенного времени может происходить случайное число каких-то событий (радиоактивных распадов, телефонных вызовов, отказов оборудования, несчастных случаев и т.п.).

Рассмотрим наиболее типичную ситуацию, в которой возникает распределение Пуассона. Пусть некоторые события могут происходить в случайные моменты времени. Определим число появлений таких событий в промежутке времени от 0 до Т.

Случайное число событий (Z), происшедших за время от 0 до Т, распределено по закону Пуассона с параметром =аТ, где а>0 – параметр задачи, отражающий среднюю частоту событий. Вероятность k появления искомых событий в течение определенного интервала времени составит

(2)

2.5. Нормальное распределение (распределение Гаусса)

Нормальный закон распределения (закон Гаусса) лежит в основе психолого-педагогических измерений, разработки тестовых шкал и методов проверки исследовательских гипотез. Нормальное (гауссовское) распределение занимает центральное место в теории и практике вероятностно-статистических исследований. В качестве непрерывной аппроксимации к биномиальному распределению его впервые рассматривал А.Муавр в 1733 г. Через некоторое время нор­мальное распределение снова открыли и изучили К.Гаусс (1809 г.) и П.Лаплас, которые пришли к нормальной функции в связи с ра­ботой по теории ошибок наблюдений.

Непрерывная случайная величина Х называется распределенной по нормальному закону, если ее плотность распределения равна

(3)

где  - математическое ожидание величины Х,

 - стандартное отклонение величины Х.

График функции нормального распределения, как видно из рисунка 1, имеет вид куполо­образной кривой.

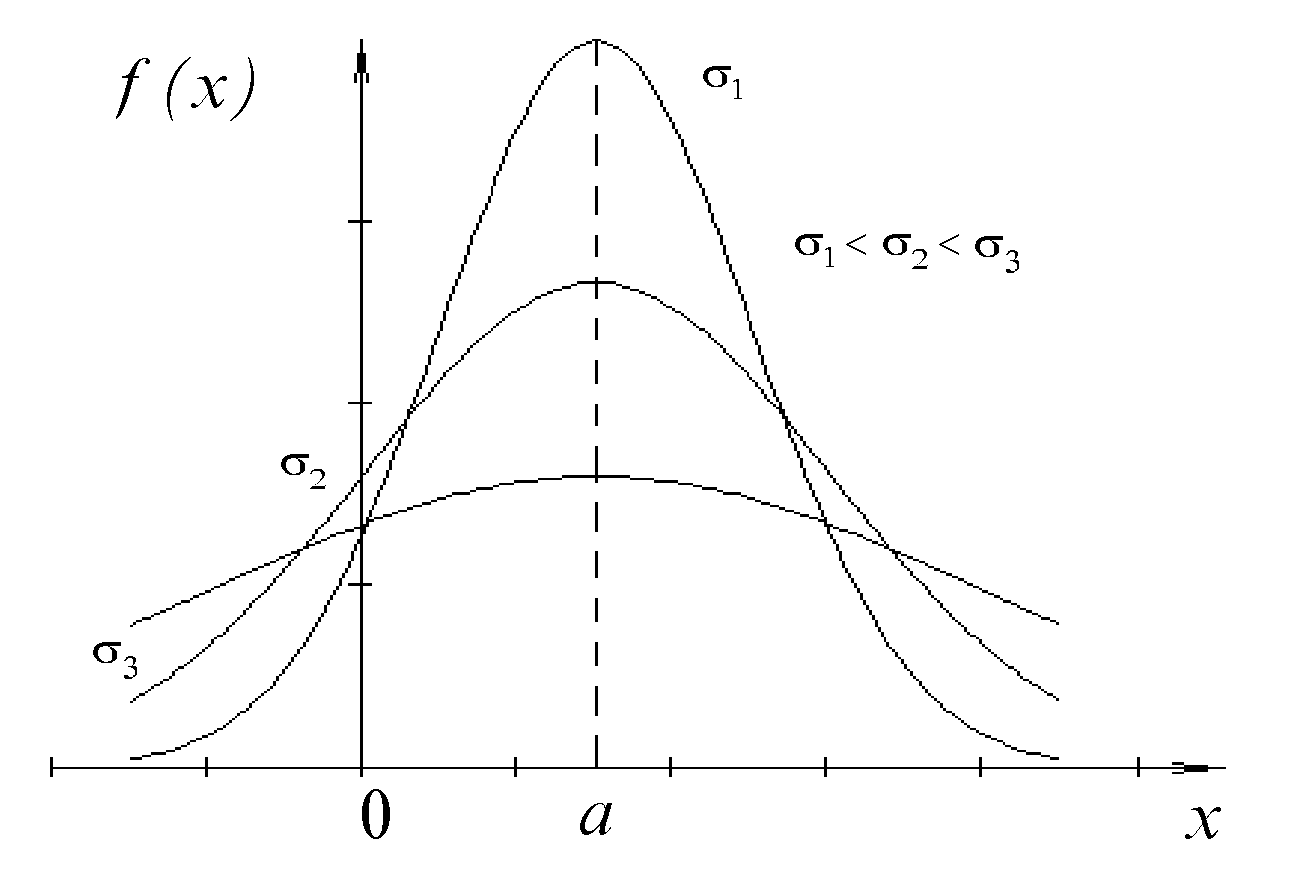
Рис.1. Распределение Гаусса (нормальное распределение).

Точка максимума имеет координаты (а; ). Ордината убывает с возрастанием значения (кривая «сжимается» к оси ОХ) и возрастает с убыванием значения  (кривая «растягивается» в положительном направлении оси ОУ). Изменение значений параметра  (при неизменном значении ) не влияет на форму кривой, а лишь перемещает кривую вдоль оси Ох.

Нормальный закон распределения изобрели для решения задач теории вероятности, но оказалось на практике, что он отлично аппроксимирует распределение частот при большом числе наблюдений для множества переменных. Опыт применения закона нормального распределения в социальных и биологических науках начинается с работы бельгийского ученого А. Кетле «Опыт социальной физики» (1835 г.). В ней он доказывал, что такие явления, как продолжительность жизни, возраст вступления в брак и появление первого ребенка подчиняются строгой закономерности. Она проявляется в том, что чаще всего встречаются средние значения соответствующих показателей, и чем больше отклонение от этой средней величины, тем реже встречаемость таких отклонений. В исследованиях А. Кетле было доказано, что распределение частот встречаемости любого демографического или антропометрического показателя, измеренного на большой выборке, имеет одну и ту же «колокообразную» форму (см. рис. 2) [1, с. 98].

Рис. 2. График распределения частот для роста 8585 взрослых людей,

родившихся в Англии в 19 в.

«Нормальным» такое распределение было названо потому, что оно наиболее часто встречалось в естественнонаучных исследованиях и казалось «нормой» распределения СВ.

Закон нормального распределения имеет целый ряд очень важных следствий, к которым мы не раз еще будем обращаться. Сейчас же отметим, что при изучении свойств выборки видится целесообразным всегда осуществлять ее проверку на нормальность. При нормальном распределении исходных данных в ходе статистического анализа применяются параметрические методы математической статистики.