Свободные гармонические колебания

Колебания, которые совершает система около положения равновесия после того, как она была выведена из состояния равновесия, носят название собственных или свободных колебаний. Свободные колебания возникают в результате достаточно быстрого изменения действующей на тело силы, т.е. воздействия, имеющего характер толчка.

Рассмотрим цилиндрическую пружины, один конец которой закреплён, а к другому подвешено тело (например, металлический шарик) массой m. Будем считать, что на тело действуют сила тяжести и сила упругости(силу сопротивления, действующую на тело при движении в реальной среде, считаем пренебрежимо малой величиной). Запишем теорему о движении центра масс тела в случае простой упругой деформации пружины – продольного растяжения (сжатия):

.

Рассмотрим задачу, в которой сила тяжести и сила упругостинаправлены вдоль одной прямой, совпадающей с осью пружины. Направив ось0Х вдоль оси пружины, получаем одномерную задачу. Теорема о движении центра масс, записанная в проекции на ось 0Х, имеет вид:

. (1)

В положении равновесия и сумма сил, действующих на шарик равна нулю. Отсюда, обозначив координату центра масс груза в положении равновесия, имеем:

; . (2)

Подставляя (2) в (1):

, но .

Следовательно:

, где или (3)

Величина Х определяет смещение груза из положения равновесия. Само положение равновесия смещается под действием силы тяжести, но это не затрагивает математическую сторону колебательного процесса.

, где , – циклическая частота и период колебаний. Период колебаний не зависит от амплитудыА (это свойство называется изохронностью колебаний).

Затухающие колебания материальной точки

Ранее мы рассматривали случаи колебаний, при которых на движущееся тело не действуют силы сопротивления. Во всякой реальной колебательной системе силы сопротивления имеются. На преодоление сопротивления затрачивается энергия колебательного движения и, в конечном счёте, колебания затухают.

Рассмотрим один из наиболее часто встречающихся на практике случаев, когда сила сопротивления пропорциональна скорости материальной точки:

.

В одномерном случае

, (4)

где r – коэффициент сопротивления. Тогда уравнение, описывающее затухающие колебания при наличии действующих на материальную точку силы упругости и силы сопротивления, будет иметь вид:

.

Введя обозначения ,, получаем следующее уравнение:

. (5)

В случае гармонического осциллятора размах колебаний, определяемый амплитудой А, остаётся постоянным. Наличие сопротивления среды приводит к тому, что размах колебаний уменьшается. Поэтому будем искать решение уравнения (5) в виде:

, (6)

где А(t) – некоторая функция времени. Продифференцировав (6) по времени, находим:

.

После подстановки этих выражений в (5) получаем:

.

Отсюда:

; ; (7)

Запишем первое уравнение в виде:

.

Проинтегрировав полученное уравнение, получим: . В результате потенцирования имеем:. Легко видеть, что:

; .

Подставим данные соотношения в (7):

.

Величина . Отсюда:

.

При условии, что , величинабудет вещественной, и решение уравнения (5) может быть представлено в виде:

З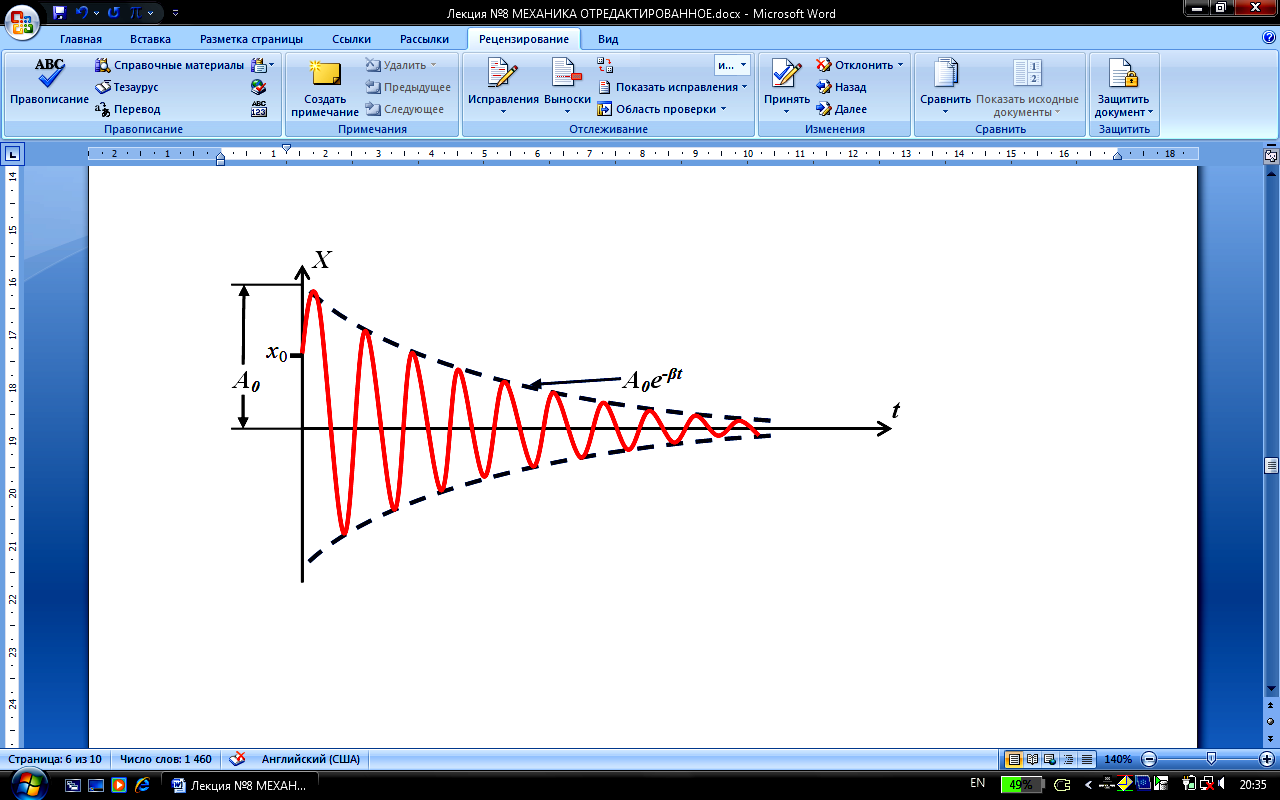десь– начальная амплитуда,– начальная фаза колебаний.

Период колебаний:

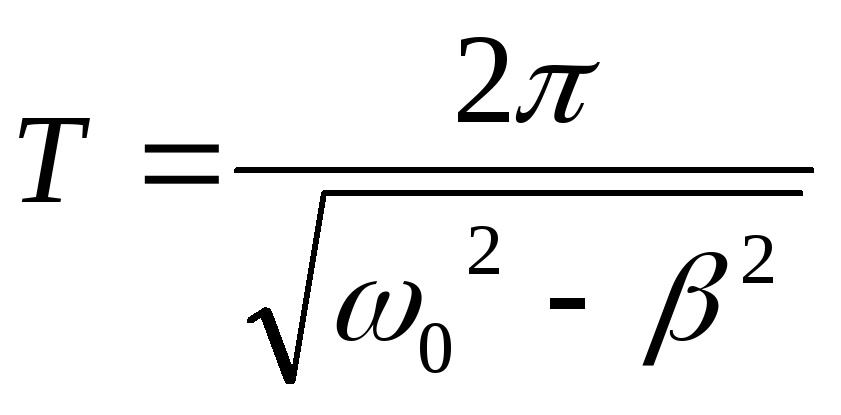. (8)

Амплитуда колебаний уменьшается по закону: (– коэффициент затухания).

При процесс перестаёт быть периодическим.

В результате затухания колебаний состояние системы () переходит в равновесие. Процесс, в результате которого параметры, характеризующие физическую систему, переходят к своим равновесным значениям, называютпроцессом релаксации. Время, в течение которого отклонения системы от равновесия уменьшается в е раз, называют временем релаксации. Найдём время релаксации :

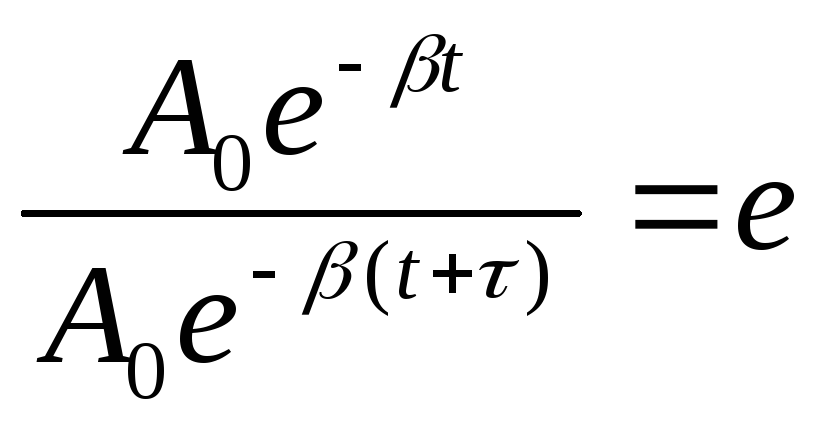или ,и.

Таким образом, коэффициент затухания есть величина обратная промежутку времени, за который амплитуда колебаний уменьшается в е раз.

Отношение двух произвольных последовательных амплитуд при затухающих колебаниях есть величина постоянная:

.

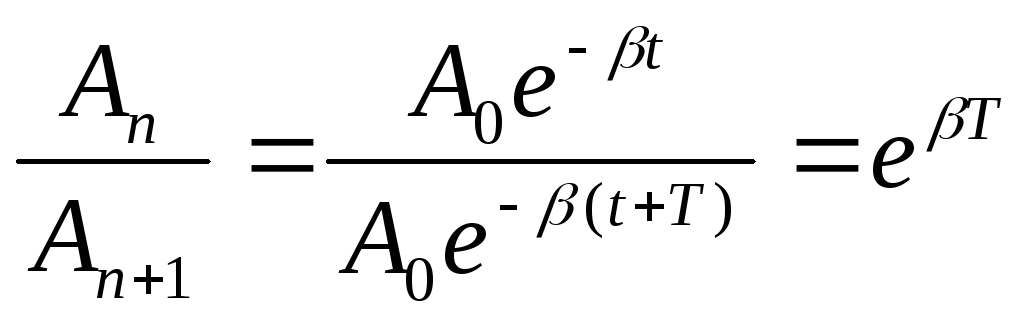Это отношение называют декрементом затухания, а логарифм этого отношения – логарифмическим декрементом затухания:

. (9)

Логарифмический декремент затухания является естественной характеристикой затухания, которая показывает, как амплитуда колебаний изменяется за один период. Тогда как коэффициент затухания определяет время, в течение которого амплитуда уменьшается ве раз.

Часто колебательные системы характеризуют также добротностью. Добротностью называют отношение энергии в системе в данный момент времени и убыли энергии за период, умноженный на .

. (10)

Поскольку энергия E(t) пропорциональна квадрату амплитуды колебаний:

.

Учитывая (9):

.

Разлагая в ряд и ограничиваясь первыми двумя членами разложения, получим:

.

Добротность системы обратно пропорциональна логарифмическому декременту затухания.