
Сумматор по модулю 2
Дискретные устройства, выполняющие операцию сложения над числами, представленными в двоичной системе счисления, называются двоичными сумматорами. Сумматор, который выполняет операцию сложения в одном разряде, называют одноразрядным.
Один из простейших логических устройств, выполняющих сложение одноразрядных чисел без переноса результата сложения в старший разряд, называется сумматором по модулю 2 или логическим элементом «Исключающее ИЛИ». На его выходе 1 появляется, когда в наборе входных сигналов содержится нечетное число 1. Графическое обозначение двухвходового сумматора по модулю 2 дано на рисунке 1.
Работу двухвходового сумматора по модулю 2 отражает таблица 1, в которой A, B — значения слагаемых. S — значение суммы.
Таблица 1
-
В
А
S
0
0
0
0
1
1
1
0
1
1
1
0
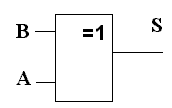
Рис. 1
Полусумматор
Полусумматор, в отличие от сумматора по модулю 2, имеет два входа А и В и два выхода: S (сумма) и P (перенос в старший разряд). Графическое обозначение полусумматора дано на рисунке 2.
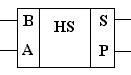
Рис. 2
Таблицей значений Р и S полусумматора является таблица 2. Перейдем к схеме полусумматора на логических элементах «Исключающее ИЛИ » и « И » (рис. 3).
Таблица 2
-
В
А
P
S
0
0
0
0
0
1
0
1
1
0
0
1
1
1
1
0

Рис. 3
Двоичный одноразрядный сумматор
Двоичный одноразрядный сумматор представляет собой дискретное устройство с тремя входами (А, В, Pn–1) и двумя выходами (S, Pn ) (рис. 4).

Рис. 4
Переменные A и В — это разряды соответственно первого и второго слагаемых; Pn–1 — значение переноса из, предыдущего разряда; S — значение разряда суммы; Pn — значение переноса в следующий разряд. Согласно правилам сложения для чисел, заданных в двоичной системе счисления, составим таблицу 3 значений Pn и S. Например, для A =1, В =0, Pn–1 имеет 1+0+1=10, следовательно, S = 0, Pn = 1; для A = B = Pn–1 =1 будет 1 +1 +1 =11, т. е. S=1 и Р = 1.
В таблице 3 А, В, Рn–1 являются аргументами, а S и Pn–1 — функциями.
Таблица 3
-
Pn–1
В
А
Pn
S
0
0
0
0
0
0
0
1
0
1
0
1
0
0
1
0
1
1
1
0
1
0
0
0
1
1
0
1
1
0
1
1
0
1
0
1
1
1
1
1
Двоичный одноразрядный сумматор может быть построен на базе двух полусумматоров и одного двухвходового логического элемента ИЛИ, соединенных между собой по схеме на рисунке 5.
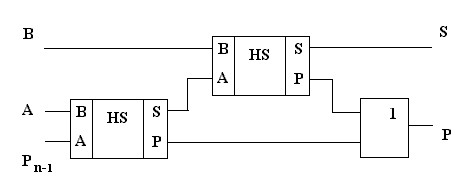
Рис. 5
Для сложения двух многоразрядных чисел объединяют соответствующее количество одноразрядных сумматоров. Схема многоразрядного сумматора приведена на рисунке 6.
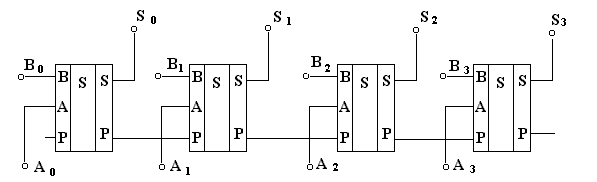
Рис. 6
В таком сумматоре В0А0, В1А1, …, Вn–1An–1 представляют входы для подачи значений соответствующих разрядов слагаемых чисел, а S0, S1 ..., Sn–1, Sn — результат сложения. Например, производится сложение двух чисел A = 1011 (11) или B =1101 (13). Тогда на вход A0 подается 1, A1 – 1, A2 – 0, A3 – 1, В0 – 1, В1—0, В2 – 1, В3 – 1. Получаем на выходах S0 – 0, S1 – 0, S2 – 0, S3 – 1, S4 – 1. Результат сложения — число 11000 (24).
