Вопросы к экзаменам / Решение уравнений средствами Excel

Решение уравнений средствами Excel

2

1. Графический способ решения нелинейных уравнений

Возьмем в качестве примера квадратное уравнение х2-5х+6=0. Для нахождения корней уравнения выполним следующие действия:

1.В ячейках А2:А22 введём значение аргумента x в диапазоне от 1,5

до 3,5 с шагом 0,1, то есть A2=1.5, A3=A2+0.1 и т. д. A22=A21+0.1, а

значение функции в ячейках B2:B10 – B2=A2^2-5*A2+6 и т. д.

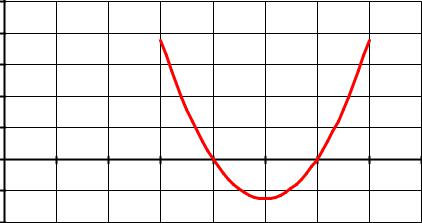
2.Используя Мастер диаграмм, тип диаграммы – точечная построим кривую функции y(x)=х2-5х+6, точки пересечения графика функции с осью абсцисс будет решением уравнения: x1=2, x2=3 (Рис.1).

Рис. 1

3

2. Подбор параметра

Когда желаемый результат вычислений по формуле известен, но неизвестны значения, необходимые для получения этого результата, можно воспользоваться средством Подбор параметра, выбрав команду Подбор параметра в меню Сервис. При подборе параметра Excel изменяет значение в одной конкретной ячейке до тех пор, пока вычисления по формуле, ссылающейся на эту ячейку, не дадут нужного результата.

Возьмем в качестве примера все то же квадратное уравнение х2-5х+6=0. Для нахождения корней уравнения выполним следующие действия:

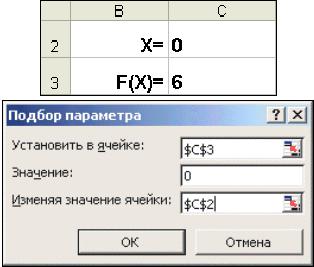
Рис. 2. Окно диалога Подбор параметра

∙В ячейку С3 (рис. 2) введем формулу для вычисления значения функции, стоящей в уравнении слева от знака равенства. В качестве аргумента используем ссылку на ячейку С2, т.е. =С2^2-5*C2+6.

∙В окне диалога Подбор параметра (рис. 2) в поле Установить в ячейке

введем ссылку на ячейку с формулой, в поле Значение - ожидаемый результат, в поле Изменяя значения ячейки - ссылку на ячейку, в

которой будет храниться значение подбираемого параметра (содержимое этой ячейки не может быть формулой).

∙После нажатия на кнопку Ok Excel выведет окно диалога Результат подбора параметра. Если подобранное значение необходимо сохранить, то нажмите на Оk, и результат будет сохранен в ячейке, заданной ранее в поле Изменяя значения ячейки. Для восстановления значения, которое было в ячейке С2 до использования команды Подбор параметра, нажмите кнопку Отмена.

4

3. Поиск решения

Команда Подбор параметра является удобной для решения задач поиска определенного целевого значения, зависящего от одного неизвестного параметра. Для более сложных задач следует использовать команду Поиск решения (Решатель), доступ к которой реализован через пункт меню

Сервис/Поиск решения.

Рассмотрим, как воспользоваться Поиском решения на примере того же квадратного уравнения.

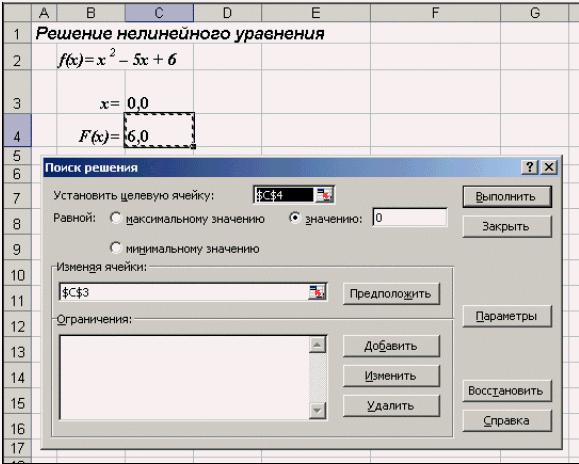
Рис. 3. Окно диалога Поиск решения

После открытия диалога Поиск решения (рис. 3) необходимо выполнить следующие действия:

1)в поле Установить целевую ячейку ввести адрес ячейки, содержащей формулу для вычисления значений оптимизируемой функции, в нашем

примере целевая ячейка - это С4, а формула в ней имеет вид: = C3^2 - 5*C3 + 6;

2)для ввода значения целевой ячейки, установить переключатель значению в положение 0;

3)в поле Изменяя ячейки ввести адреса изменяемых ячеек, т.е. аргументов целевой функции ($С$3) (или щелкая мышью при нажатой клавише Сtrl на соответствующих ячейках), для автоматического

поиска всех влияющих на решение ячеек используется кнопка

Предположить;

5

4)в поле Ограничения с помощью кнопки Добавить ввести все ограничения, которым должен отвечать результат поиска: для нашего примера ограничений задавать не нужно;

5)для запуска процесса поиска решения нажать кнопку Выполнить.

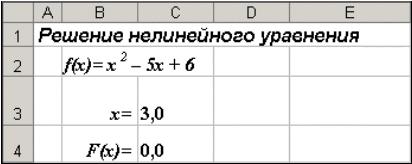
Рис. 4. Результаты поиска

Для сохранения полученного решения необходимо использовать переключатель Сохранить найденное решение в открывшемся окне диалога Результаты поиска решения. После чего рабочий лист примет вид, представленный на рис. 4. Полученное решение зависит от выбора начального приближения, которое задается в ячейке С4 (аргумент функции). Если в качестве начального приближения в ячейку С4 ввести значение, равное 1,0, то с помощью Поиска решения найдем второй корень, равный 2,0.

6

4. Решение систем линейных уравнений методом Крамера

Решение систем линейных уравнений рассмотрим на примере системы трёх линейных уравнений

Решения системы уравнений будет определяться следующими соотношениями:

x = x = 2,5 ; y = y = -7 ; z = z = 4,5 .

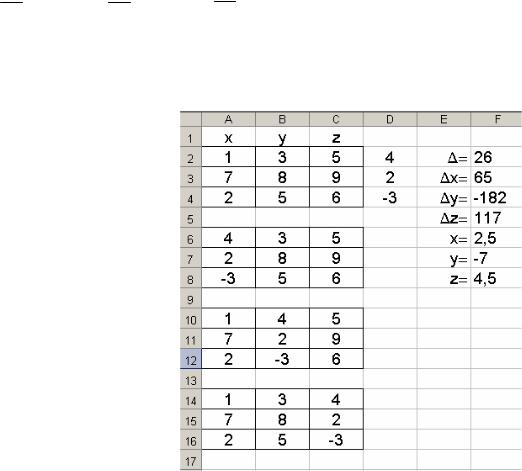
Для решения системы линейных уравнений в табличном процессоре MS Excel запишем главный определитель в ячейки A2:C4, дополнительные

– x в ячейки A6:C8, y – A10:C12, z – A14:C16. Тогда определители можно найти с помощью функции МОПРЕД:

F2 =МОПРЕД(A2:C4);

F3=МОПРЕД(A6:C8);

F4=МОПРЕД(A10:C12)

F5=МОПРЕД(A14:C12)

Решение системы уравнений будет равно:

x=F3/F2;

y=F4/F2;

z=F5/F2.

7

5. Решение систем линейных матричным способом

Воспользуемся предыдущей системой линейных уравнений:

ì x + 3y + 5z = 4 ïí 7 x + 8 y + 9z = 2

ïî2x + 5 y + 6 z = -3

Данную систему линейных уравнений можно записать в матричной форме:

Решение будем искать из уравнения вида:

X = A−1 × B , где A−1 – обратная матрица матрице A.

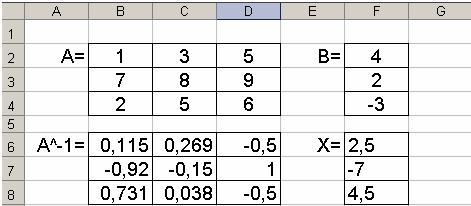
Для системы в Excel запишем коэффициентов при неизвестных в ячейках B2:D4, матрицу столбец – F2:F4 (рис. 5).

Рис. 5

Тогда с помощью функции =МОБР(B2:D4) можно найти обратную матрицу A−1 , для чего:

1.В ячейке B6 введите функцию МОБР(B2:D4).

2.Выделите диапазон ячеек B6:D8.

3.Нажмите клавишу F2.

4.Нажмите комбинацию клавиш Shift+Ctrl+Enter.

Для нахождения решения системы уравнений надо перемножить матрицу A−1 на матрицу-столбец B . Для этого:

1.В ячейке F6 введите функцию =МУМНОЖ(B6:D8;F2:F4).

2.Выделите диапазон ячеек F6:F8.

3.Нажмите клавишу F2.

4.Нажмите комбинацию клавиш Shift+Ctrl+Enter.

8

6. Варианты заданий

ì x1 + x2 + 2x3 = −1

23.ïí2x1 - x2 + 2x3 = -4 ïî4x1 + x2 + 4x3 = -2