
28-04-2013_17-44-42(1) / 1
.doc
|
16.Средняя гармоническая величина. Средняя гармоническая – это величина, обратная средней арифметической. В зависимости от формы представления исходных данных средняя гармоническая может быть рассчитана как простая и как взвешенная. При работе со сгруппированными данными используется средняя гармоническая взвешенная. Когда статистическая информация не содержит частот по отдельным вариантам совокупности, а представлена как их произведение, применяется формула средней гармонической взвешенной. Средняя гармоническая взвешенная используется в тех случаях, когда известен числитель исходного соотношения средней, но не известен знаменатель. Если известен ряд вариант (х) и ряд произведений вариант на частоту (xf = M), а сама частота (f) неизвестна, расчет средней производится по средней гармонической взвешенной:
Если исходные данные несгруппированны, то применяется средняя гармоническая простая. Средняя гармоническая простая используется при М = const:
Среднюю гармоническую простую называют еще средней из обратных значений признаков. С помощью гармонической средней в статистике определяется средний % выполнения плана (по данным фактического выполнения плана), средние затраты времени на выполнение операций (по данным о средних затратах времени на одну операцию и общее время работы по отдельным работникам) и т.д.
|
17.Структурные средние (мода и медиана). Мода — это количественное значение,(кол-я характеристика) статистической единицы, которая наиболее часто встречается в данной совокупности. Для того чтобы рассчитать моду надо сгруппировать ед. статистические, наблюдаемые. Найти наибольшую частоту и соответствующей этой частоте значение признака и будет модой. Если группировка представлена в виде интервала, то мода рассчитывается по формуле:
где:
Медиана — это значение признака, у той стат-ой ед., которая находится в середине ряда. Для того чтобы найти медиану надо разделить сумму частот на 2 и определить порядковый № той стат-й ед., которая находится в середине При вычислении медианы для интервального вариационного ряда сначала определяют медианный интервал, в пределах которого находится медиана, а затем — значение медианы по формуле:
где:
|
18.Показатели вариации и методики их расчеты.
Вариация признака
– различие индивидуальных значений
признака внутри изучаемой совокупности.
Она возникает в результате того, что
его индивидуальные значения складываются
под совокупным влиянием разнообразных
факторов (условий), которые по-разному
сочетаются в каждом отдельном случае.
Колебания отдельных значений
характеризуют показатели вариации.
К абсолютным
показателям
относятся: • размах
вариации (R)
– показатель, показывающий насколько
велико различие между единицами
совокупности, имеющими наибольшее и
наименьшее значение признака: R
= xmax
- xmin;
• среднее
линейное отклонение (
• дисперсия
– средний квадрат отклонений
индивидуальных значений признака от
их средней величины:
• среднее
квадратическое отклонение
– это корень квадратный из дисперсии
К относительным показателям относятся:
• коэффициент
осцилляции
показывает относительную колеблемость
крайних значений признака вокруг
средней:
• относительное
линейное отклонение
характеризует долю усредненного
значения абсолютных отклонений от
средней величины:
• коэффициент
вариации
– показатель колеблемости для оценки
типичности средней величины, если <
40%, то совокупность однородная,
колеблемость признаков умеренная:
|
19.Дисперсия, её свойства и методы расчеты Дисперсия – средний квадрат отклонений, определяемый как средняя из отклонений, возведенных в квадрат.
Для
несгруппированных данных :
Дисперсия обладает
рядом свойств, которые позволяют
упростить ее расчеты. 1. Если из всех
значений вариант отнять какое-то
постоянное число А, то средний квадрат
отклонений от этого не изменится:
2. Если все значения вариант разделить на какое-то постоянное число А, то средний квадрат отклонений уменьшится от этого в А² раз, а среднее квадратическое отклонение – в А раз:
3. Дисперсия,
рассчитанная от постоянной величины,
больше дисперсии, рассчитанной от
средней, на квадрат разности между
средней величиной и постоянной, т.е.
на
4. Дисперсия от средней имеет свойство минимальности, т.е. она всегда меньше дисперсий, исчисленных от любых других величин. В этом случае, когда А = 0 формула принимает вид:
|
20.Понятие о выборочном наблюдении.
Выборочное
наблюдение
основывается
на применении выборочного метода
статистического исследования. Сущность
выборочного наблюдения состоит в том,
что обследованию подвергается только
часть совокупности, отобранная по
особым правилам: должен действовать
принцип случайного непредвзятого
отбора; в выборочную совокупность
должны попасть представители всех
групп, имеющихся в генеральной
совокупности; выборочная совокупность
должна полно воспроизводить
закономерности, присущие всей
генеральной совокупности.Генеральная
совокупность – вся совокупность, из
которой проводится отбор; отобранные
данные из генеральной являются
выборочной совокупностью или выборкой.
Необходимая численность выборки
рассчитывается по соответствующим
математическим формулам. Виды выборочных
работ: • демографическое обследование;
• социологическое обследование,
опросы; • проверка качества готовой
продукции; • определение потерь
рабочего времени путем фотографии
рабочего дня и др. Значение
выборочного метода:
при минимальной численности исследуемых
единиц проведение статистического
исследования будет происходить в
более короткие промежутки времени и
с наименьшими затратами средств и
труда.В выборочном наблюдении используют
следующие условные обозначения: 1.
Генеральная совокупность: а)средняя
величина - Различают 2 вида выборочного наблюдения: повторный и бесповторный. При бесповторном отборе отобранная единица не возвращается в совокупность, при повторном – возвращается и снова может быть выбранной.
|
|
30.Агрегатные индексы.
Общие индексы
(I)
характеризуют изменение совокупности
в целом. Основной формой общих индексов
являются агрегатные
индексы.
Агрегатным он называется потому, что
числитель и знаменатель его представляют
набор разнородных элементов. Агрегатный
индекс рассчитывается как отношение
суммы произведений индексируемых
величин сравниваемых периодов на веса
(величины, с помощью которых суммируются
разнородные элементы). К агрегатным
индексам относятся индексы:
физического
объема продукции
|
29.Общее понятие об индексах. Индивид индексы. Индекс – это относит.показатель сравнения сложных общественных явлений во времени, с планом или в пространстве, элементы которого не поддаются суммированию. Индекс получает название по названию индексируемой величины. Каждая индексируемая величина имеет свое обозначение: p – цена, z – с/с, q – физический объем, T – численность работающих (затраты времени), w – выработка, t – трудоемкость.
Для определения
индекса надо произвести сопоставление
не менее 2 величин, отражающих изменения
индексируемого показателя. Уровни
базисного периода обозначаются 0,
отчетного – 1. Индексы выражаются в
коэффициентах (базовый уровень принят
за 1) или в % (когда он принят за 100).
Сферы
применения индексного метода:
•
сравнительная характеристика сложных
совокупностей; •
анализ динамики средних показателей,
зависящих от изменения структуры
совокупности; •
изучение связей и оценка доли отдельных
факторов в изменении сложного явления.
Классификация
индексов:
• по степени
охвата явления:
индивидуальные, общие, групповые; •
по виду весов;
• по базе
сравнения:
базисные,
цепные, территориальные, плановые; •
по форме и
методам построения:
агрегатные, средние, средних величин;
• по объекту
исследования:
цен, производительности труда,
себестоимости, физического объема
продукции. Индивидуальные
индексы (i)
характеризуют изменение более или
менее однородных объектов, входящих
в состав сложного явления: цен
|
28.Изучение сезонных колебаний.
Сезонные
колебания
– периодические
колебания, возникающие под влиянием
смены времени года и
других причин природного или
социально-культурного
порядка. Для анализа рядов динамики
используются специальные методы,
позволяющие установить и описать
особенности изменения уровней ряда.
Изменения сезонных колебаний
производится с помощью индексов
сезонности Is:
1. Способ
переменной средней
– для рядов с ярко выраженной тенденцией
развития:
3. Методом
скользящей средней:
1 этап. Определение основной тенденции развития по квартальным данным методом скользящей средней для исключения ее из динамического ряда. 2 этап. Расчет сезонных колебаний. 3 этап. Расчет средних сезонных колебаний для исключения их из динамического ряда.
|
40.Понятие и состав национального богатства Национальное богатство представляет собой совокупность материальных благ созданных обществом за весь период его существования. Сюда же включены вовлечённые в хозяйственный оборот природные ресурсы. Национальное богатство выступает важнейшим фактором и необходимым условием процесса воспроизводства. Этим и обусловлено место данного показателя в системе экономических показателей. В соответствии с принятой в отечественной статистике классификацией в состав национального богатства включают: • основные фонды; • материальные оборотные средства; • домашнее имущество населения; • вовлекаемые в народнохозяйственный оборот природные ресурсы. В соответствии с международной классификацией в состав НБ включают: • землю; • человеческий фактор; • финансовые активы. Отличительная черта национального богатства – в составе национального богатства запасы и резервы учитываются отдельно по месту их определения и продолжительности сохранения. В статистике расчет показателя национального богатства обычно осуществляется по состоянию на начало и конец года. В изучении национального богатства значительное место отведено стоимостным группировкам. Статистика производит группировку национального богатства по следующим признакам: 1) натурально-вещественному составу; 2) отраслям экономики; 3) секторам экономики; 4) формам собственности; 5) административно-территориальному признаку. Статистические данные национального богатства дают экономическую оценку стране в целом, ее имущественному положению, а также показывают, насколько экономический потенциал страны соответствует международным стандартам. Они передают уровень развития страны в международных масштабах. Рост национального богатства является одним из главных факторов экономического роста страны.
|
29.Общее понятие об индексах. Индивидуальные индексы. Индекс – это относит.показатель сравнения сложных общественных явлений во времени, с планом или в пространстве, элементы которого не поддаются суммированию. Индекс получает название по названию индексируемой величины. Каждая индексируемая величина имеет свое обозначение: p – цена, z – с/с, q – физический объем, T – численность работающих (затраты времени), w – выработка, t – трудоемкость.
Для определения
индекса надо произвести сопоставление
не менее 2 величин, отражающих изменения
индексируемого показателя. Уровни
базисного периода обозначаются 0,
отчетного – 1. Индексы выражаются в
коэффициентах (базовый уровень принят
за 1) или в % (когда он принят за 100).
Сферы
применения индексного метода:
•
сравнительная характеристика сложных
совокупностей; •
анализ динамики средних показателей,
зависящих от изменения структуры
совокупности; •
изучение связей и оценка доли отдельных
факторов в изменении сложного явления.
Классификация
индексов:
• по степени
охвата явления:
индивидуальные, общие, групповые; •
по виду весов;
• по базе
сравнения:
базисные,
цепные, территориальные, плановые; •
по форме и
методам построения:
агрегатные, средние, средних величин;
• по объекту
исследования:
цен, производительности труда,
себестоимости, физического объема
продукции. Индивидуальные
индексы (i)
характеризуют изменение более или
менее однородных объектов, входящих
в состав сложного явления: цен
|
|
21.Ошибки выборочного наблюдения.
Неточности,
неправильности в статистических
данных, полученных при наблюдении,
принято называть ошибками наблюдения.
Эти ошибки подразделяются на два вида:
ошибки регистрации и ошибки
репрезентативности (представительности
наблюдения). Ошибки регистрации –
это расхождения между сведениями,
записанными в формуляры наблюдения
и фактическим положением в исследуемой
совокупности. Ошибки репрезентативности
(представительности) – это расхождение
между характеристиками выборки и
генеральной совокупности. Ошибка
рассчитывается по формуле:
Рассчитывают 2 вида ошибок: среднюю (µ) и предельную (∆). Повторный для средней:
Бесповторный для средней
С заданной
вероятностью P(t)
находится предельная ошибка выборки:
где t – коэффициент доверия, определяется исходя из вероятности исследования; ∆x – предельная ошибка выборки. На практике пользуются готовыми таблицами значений.
Доверительные
пределы, в которых следует ожидать
генеральную среднюю:
|
22. Понятие о динамических рядах, их виды и правила построения. Ряд динамики – ряд расположенных в хронологической последовательности признаков каких-то значений. Ряды динамики показывают изменение процесса или явления во времени. Любой ряд динамики имеет 2 основных элемента: 1) t – показатель времени; 2) Yt – соответствующие им уровни ряда (уровни развития изучаемого явления). Уровни рядов динамики должны быть сопоставимы между собой. Для несопоставимых величин нельзя вести расчеты показателей рядов динамики. Ряды динамики различаются по видам: в зависимости от формы выражения уровней (Yt): • абсолютные; • относительные; • средние.• в зависимости от формы выражения показателя времени в статике: • моментные; • интервальные. Задачи, решаемые с помощью рядов динамики: 1) характеристика уровней показателей, изучаемых явлений во времени; 2) анализ динамики изучаемых явлений; 3) выявление основных тенденций развития (тренда); 4) изучение периодических колебаний; 5) интерполяция (определение недостающих данных) и экстраполяция (прогнозирование). Ряды динамики представляют в виде таблицы или графически. При графическом изображении ряда динамики (динамического ряда) на оси абсцисс строится шкала времени, а на оси ординат – шкала уравнений ряда (арифметическая или иногда логарифмическая).
|
23.Средние показатели рядов динамики. Для получения обобщающих показателей динамики социально-экономических явлений определяются средние величины ряда динамики: 1. При расчете среднего уровня ряда динамики исходят из вида ряда динамики:
• в интервальных
рядах – по средней арифметической
простой:
• в моментном
динамическом ряду с равными
промежутками времени между датами –
по средней хронологической:
• в моментном
ряду с неравными
промежутками времени между датами –
по средней арифметической взвешенной
• когда известны
уровни на начало и конец периода –
средний уровень равен половине их
сумм. 2. Средний
абсолютный прирост
– обобщающий показатель скорости
абсолютного изменения уровней
динамического ряда:
3. Средний
темп роста
– обобщающая характеристика
индивидуальных темпов роста ряда
динамики:
4. Средний
темп прироста
определяется на основе взаимосвязи
между темпами роста и прироста по
формуле:
|
24.Аналитические показатели рядов динамики. Для изучения интенсивности изменения уровней ряда во времени исчисляются аналитические показатели динамики. Эти показатели исчисляют 2 методами: • цепным – каждый последующий уровень сравнивается с предыдущим; • базисным – сравнивается с одним и тем же уровнем, принятым за базу сравнения. Большой проблемой является выбор базы сравнения. База сравнения – это наиболее характерный период в развитии изучаемого социально-экономического явления. 1.Абсолютный прирост: - базисный ∆Yб = Yi –Y0 цепной∆Yц = Yi –Yi-1
2.Темп роста: баз-й
Tб
3.Темп прироста: базисный Т∆б = Тб – 1 цепной Т∆ц = Тц – 1.
4. Абсолютное
значение 1% прироста К1%
Между базисными и цепными показателями динамики существует взаимосвязь: сумма цепных абсолютных приростов равна соответствующему базисному приросту: ∑∆Yцi = ∑∆Yбi • произведение цепных темпов роста равно соответствующему базисному: Тц1 × Тц2 × … × Тцi = Тбi
|
|

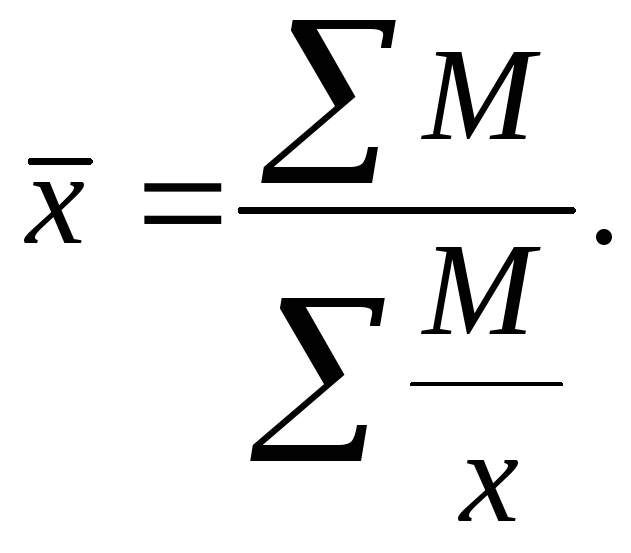
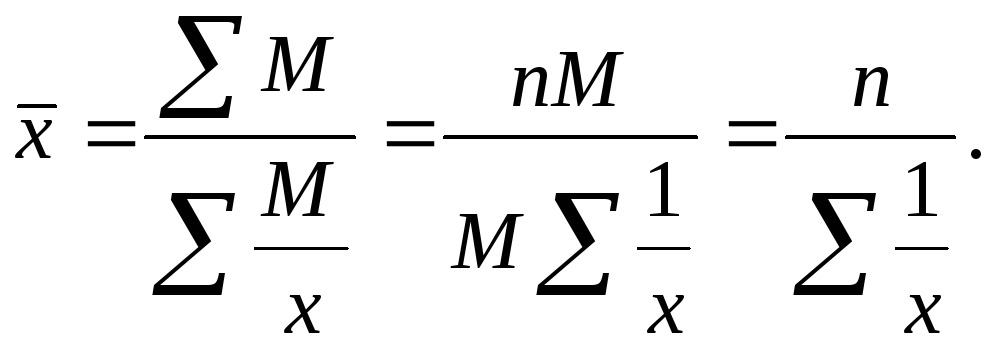
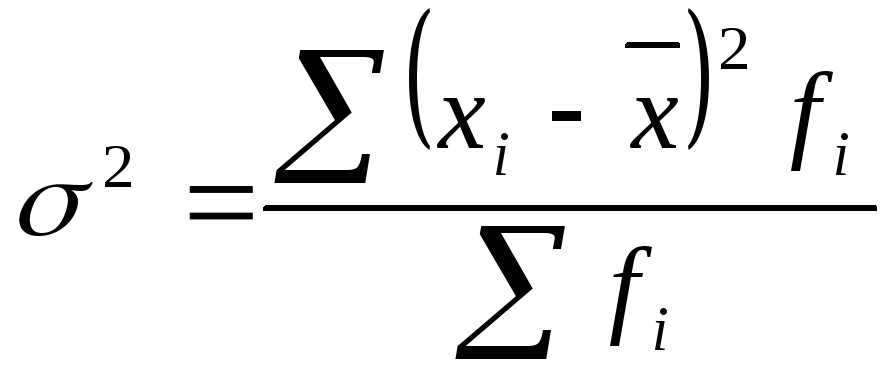 –
для сгруппированных;
–
для сгруппированных;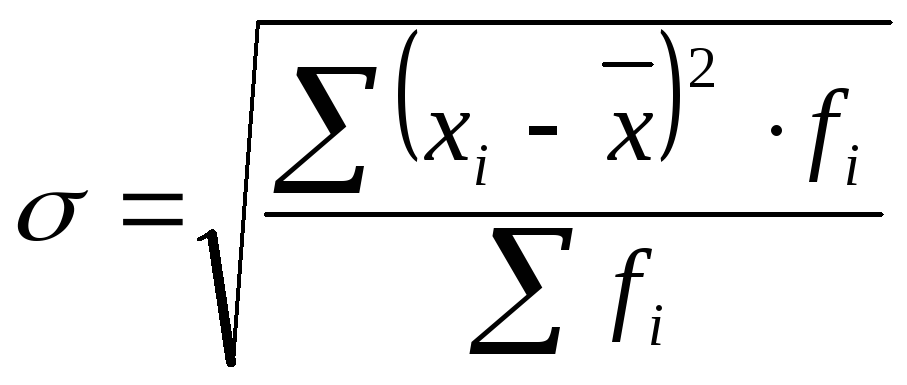 .
.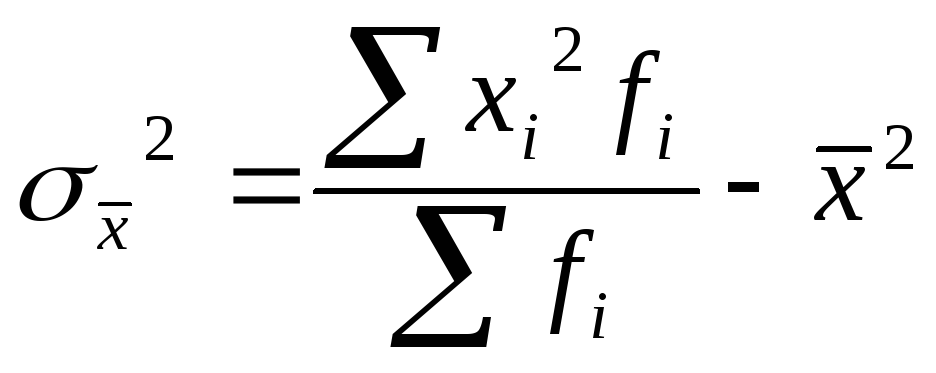 или
или 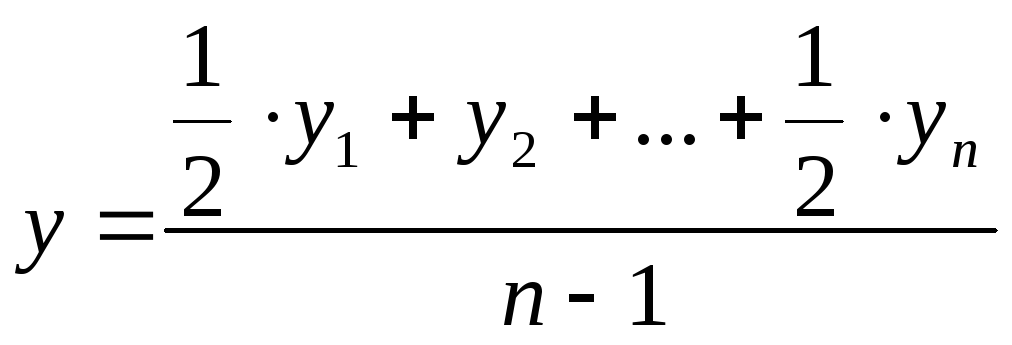 ,
где n
– число уровней;
,
где n
– число уровней;