
ПиРЭЭ_Kурс—Лекции
.pdf
Для сталеалюминиевых проводов õ0 определяется по справочным таблицам в зависимости от сечения, для стальных - в зависимости от сечения и тока.
Активная проводимость линии соответствует двум видам потерь активной мощности: от тока утечки через изоляторы и на корону.
Токи утечки через изоляторы малы, и потерями мощности в изоляторах можно пренебречь. В воздушных линиях напряжением 110 кВ и выше при определенных условиях напряженность электрического поля на поверхности провода возрастает и становится больше критической. Воздух вокруг провода интенсивно ионизируется, образуя свечение - корону. Короне соответствуют
потери активной мощности. Наиболее радикальным средством снижения потерь мощности на
корону является увеличение диаметра провода. В связи |
этим задаются |
наименьшие |
допустимые сечения по короне: на 110 кВ-70 ìì 2 , 150 кВ-120 ìì |
2 , 220кВ-240 ìì |
2 . |
При расчете установившихся режимов сетей до 220 кВ активная проводимость практически не учитывается. В сетях с U íîì ≥ 330 кВ при определении потерь мощности, при расчете оптимальных режимов необходимо учитывать потери на корону. Обычно при этом учитываются различные виды зависимости потерь на корону от напряжения.
Емкостная проводимость линии bë обусловлена емкостями между проводами разных фаз и
емкостью провод - земля и определяется следующим образом: |
|
bë = b0 l , |
(5.1.6) |
где b0 - удельная емкостная проводимость, См/км, которая может быть определена по
справочным таблицам или по следующей формуле: |
|
||
b = |
7.58 |
10 −6 . |
(5.1.7) |
|
|||
0 |
Dñð |
|
|
|
|
|
|
lg rïð
Для большинства расчетов в сетях 110-220 кВ линия электропередачи обычно представляется более простой схемой замещения (рис. 5.1.3, 6). В этой схеме вместо емкостной проводимости (рис.5.1.3, а) учитывается реактивная мощность, генерируемая емкостью линий. Половина емкостной мощности линии, МВАр, равна
|
Q |
|
= 3I U |
= 3U 2 |
1 |
b |
l = |
1 |
U 2 b |
|
, |
(5.1.8) |
|
|
|
|
|
||||||||
|
|
ñ |
ñ ô |
ô |
2 0 |
2 |
|
ë |
|
|
||
где U ô |
и U -фазное и междуфазное |
напряжение, кВ; |
Iñ |
- емкостный ток на землю, |
||||||||
I c = U ô bë |
/ 2 . |
|
|
|
|
|
|
|
|
|
|
|
Из (5.1.8) следует, что мощность Qc , генерируемая линией, сильно зависит от напряжения. Чем выше напряжение, тем больше емкостная мощность.
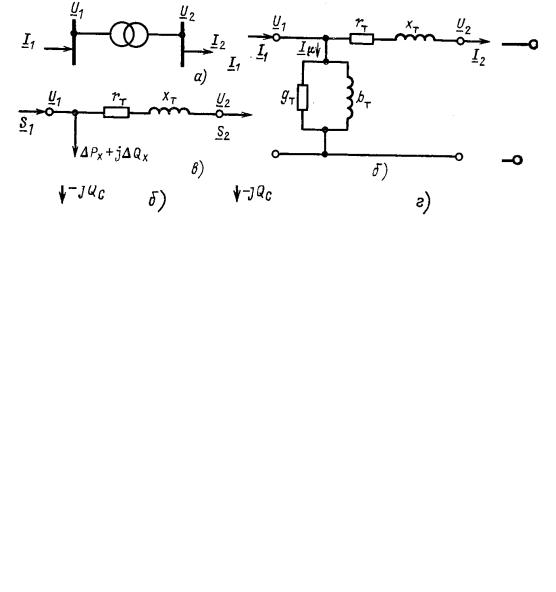
Рис. 5.1.3. Схемы замещения линий электропередачи:
а ,б - воздушная линия 110-330 кВ с емкостной проводимостью и с реактивной мощностью, генерируемой емкостью линий; в - воздушная линия Uíîì ≤ 35 кВ; г - кабельная
линия U |
íîì |
≤ 10 кВ |
|
|
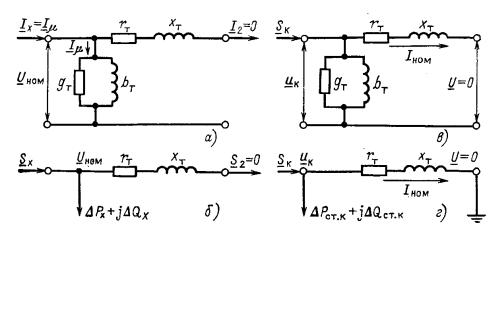
Рис. 5.2.1. Двухобмоточный трансформатор а - условное обозначение; б - Г-образная схема замещения; в - упрощенная схема замещения
Для воздушных линий напряжением 35 кВ и ниже емкостную мощность можно не учитывать (рис. 5.1.3, б). Для линий U íîì ≥ 330 кВ при длине более 300-400 км для определения параметров П-образной схемы замещения учитывают равномерное распределение сопротивлений и проводимостей вдоль линии.
Кабельные линии электропередачи представляют такой же П-образной схемой замещения, что и воздушные линии (рис.5.1.1). Удельные активные и реактивные сопротивления r0 , õ0
определяют по справочным таблицам, так же как и для воздушных линий. Из (5.1.3), (5.1.7) видно, что õ0
уменьшается, а b0 растет при сближении фазных проводов. Для кабельных линий расстояния между проводами значительно меньше, чем для воздушных, и õ0 очень мало. При расчетах режимов для кабельных сетей напряжением 10 кВ и ниже можно учитывать только активное сопротивление (рис. 5.1.3,г). Емкостный ток и Qc в кабельных линиях больше, чем в воздушных. В кабельных линиях высокого напряжения учитывают Qc (рис. 5.1.3,6), причем удельную емкостную мощность Qc0 , квар/км, можно определить по таблицам. Активную
проводимость g ë учитывают для кабелей 110 кВ и выше. Удельные параметры схемы замещения кабеля r0 , õ0 , а также Qc0 , приведенные в справочных таблицах, ориентировочны, более точно их можно определить по заводским характеристикам кабеля.
5.2. Схемы замещения трансформаторов и автотрансформаторов
Двухобмоточный трансформатор (рис. 5.2.1, а) можно представить в виде Г-образной схемы замещения (рис.2.4, б). Продольная часть схемы замещения содержит rÒ и õÒ - активное и реактивное сопротивления трансформатора. Эти сопротивления равны сумме соответственно активных и реактивных сопротивлений первичной и приведенной к ней вторичной обмоток. В такой схеме замещения отсутствует трансформация, т. е. отсутствует идеальный трансформатор, но сопротивление вторичной обмотки приводится к первичной. При этом приведении сопротивление вторичной обмотки умножается на квадрат коэффициента трансформации. Если сети, связанные трансформатором, рассматриваются совместно, причем параметры сетей не приводятся к одному базисному напряжению, то в схеме замещения трансформатора учитывается идеальный трансформатор.
Поперечная ветвь схемы (ветвь намагничивания) состоит из активной и реактивной проводимостей gÒ и bÒ . Активная проводимость соответствует потерям активной мощности в стали трансформатора от тока намагничивания I (рис. 5.2.1, б). Реактивная проводимость
определяется магнитным потоком взаимоиндукции в обмотках трансформатора.
В расчетах электрических сетей двухобмоточные трансформаторы при U â.íîì ≤ 220 кВ представляют упрощенной схемой замещения (рис. 5.2.1, в). В этой схеме вместо ветви намагничивания учитываются в виде дополнительной нагрузки потери мощности в стали
трансформатора или потери холостого хода |
Px + j Qx . |
|
Для каждого трансформатора известны следующие параметры (каталожные данные): Síîì |
- |
|
номинальная мощность, МВ·А; U â.íîì ,U í .íîì |
-номинальные напряжения обмоток высшего |
и |
низшего напряжений, кВ; Põ - активные потери холостого хода, кВт; I õ % -ток холостого хода,
% I íîì ; |
Pê -потери короткого замыкания, кВт; U ê |
% -напряжение короткого замыкания, % |
U íîì . |
По |
этим |
данным можно определить все параметры схемы замещения трансформатора (сопротивления и проводимости), а также потери мощности в нем.
Проводимости ветви намагничивания определяются результатами опыта холостого хода (XX). В этом опыте размыкается вторичная обмотка, а к первичной подводится номинальное напряжение. Ток в продольной части схемы замещения равен нулю, а к поперечной приложено U íîì (рис. 5.2.2, а). Трансформатор потребляет в этом режиме только мощность, равную потерям холостого хода, т. е. (рис. 5.2.2, б)
S õ = |
|
Põ |
+ j |
Qõ . |
|
|
|
Проводимости, См, определяются следующими выражениями: |
|
||||||
g |
Ò |
= |
P / U 2 |
, |
(5.2.1) |
||
|
|
x |
íîì |
|
|
||
b |
|
= |
Q |
x |
/ U 2 |
, |
(5.2.2) |
Ò |
|
|
íîì |
|
|
||
где напряжения выражены в киловольтах, а мощности в мегаваттах и мегаварах.
Потери активной мощности в стали определяются в основном напряжением и приближенно предполагаются независящими от тока и мощности нагрузки ( I 2 и S2 ). В схеме на рис. 5.2.1, б
Px постоянна и равна каталожному значению. Ток намагничивания в трансформаторе имеет очень маленькую активную составляющую:
I = I x ≈ I ′x′ ,
где I ′′ - реактивная составляющая I |
x |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Поэтому |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q |
|
= 3I ′′U |
|
|
3I |
U |
|
|
|
I |
x |
0 |
I |
íîì |
U |
|
|
I |
x |
0 |
S |
íîì |
|
|
|
|
|
≈ |
|
|
= 3 |
|
0 |
|
|
= |
|
0 |
|
(5.2.3) |
||||||||||
|
x |
íîì .ô |
íîì |
.ô |
|
|
|
|
|
íîì .ô |
|
|
|
|
|
||||||||||
|
|
x |
|
|
x |
|
|
|
|
100 |
|
|
|
|
100 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Отметим, что |
Px намного меньше, чем |
|
Qx , и полная мощность трансформатора в режиме |
||||||||||||||||||||||
холостого хода Sx |
приближенно равна намагничивающей мощности |
Qx . |
|
||||||||||||||||||||||
Рис. 5.2.2. Схемы опытов холостого хода и короткого замыкания: а, б - опыт холостого хода: в, г - опыт короткого замыкания
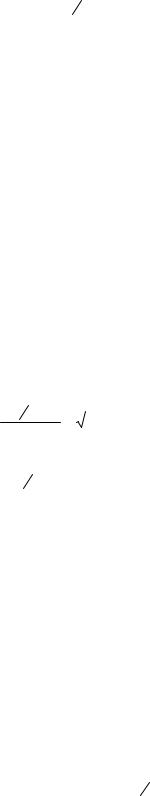
С учетом (5.2.3) проводимость bÒ определяется так:
bÒ = |
I x |
0 0 |
Síîì |
(5.2.2а) |
|
100U íîì2 |
|||||
|
|
||||
Сопротивления трансформатора rÒ и õÒ определяются по результатам опыта короткого замыкания (КЗ). В этом опыте замыкается накоротко вторичная обмотка, а к первичной обмотке подводится такое напряжение, при котором в обеих обмотках трансформатора токи равны номинальному. Это напряжение и называется напряжением короткого замыкания uk
(рис. 5.2.2,6 и г). Потери в стали в опыте короткого замыкания |
PÑÒ.ê очень малы, так как uk |
|||||||
намного меньше U íîì |
. Поэтому приближенно считают, что все потери мощности в опыте КЗ |
|||||||
Pê |
идут |
|
|
|
|
|
на |
нагрев |
обмоток трансформатора, т. е. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S 2 |
|
|
|
P |
= 3I 2 |
r = |
íîì |
r , |
(5.2.4) |
||
|
|
|||||||
|
ê |
|
íîì |
Ò |
|
U íîì2 |
Ò |
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
P U 2 |
|
|
|
|
|
|
rÒ |
= |
ê |
íîì |
. |
|
|
(5.2.5) |
|
S íîì2 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
В современных мощных трансформаторах rÒ « õÒ
uk = uk 0 0 U íîì
100
и u |
k |
≈ u′′ . Из опыта КЗ (рис.5.2.3, в) |
|||
|
|
|
k |
||
|
|
|
|
||
≈ 3I íîì |
õÒ . |
||||
Умножая последнее выражение на U íîì |
, после преобразований получим |
|
|
õÒ = |
uk 0 0 U íîì2 |
(5.2.6) |
|
|
. |
||
|
|||
|
100Síîì |
|
|
В (5.2.5), (5.2.6) сопротивления получаются в омах при подстановке напряжений в киловольтах, а мощностей - в мегавольт-амперах и в мегаваттах.
Потери активной мощности в rÒ зависят от тока и мощности нагрузки I 2 и S2 . Эти потери равны
P |
= 3I 2r = |
S 2 |
r . |
|
2 |
||||
U 2 |
||||
|
2 |
|
||
|
|
2 |
|
Если подставить в последнее выражение r из (5.2.5) и учесть, что U 2 |
≈ U 2 |
||
Ò |
2 |
íîì |
|
|
P S 2 |
|
|
P = |
k 2 |
. |
|
|
|
||
Ò |
S íîì2 |
|
|
|
|
||
Потери реактивной мощности в õÒ аналогично (5.2.6) определяются так:
, то получим
(5.2.6)
|
|
|
|
S 2 |
|
|
|
|
|
|
u |
k |
0 |
S |
2 |
|
|
|
Q = 3I 2 |
õ = |
2 |
|
õ |
|
= |
|
|
0 |
|
|
2 |
|
(5.2.7) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Ò |
2 |
Ò |
U 2 |
Ò |
|
|
100S |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
íîì |
|
|
|
|||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
Для трансформатора, через который проходят ток |
нагрузки |
|
I2 и мощность |
S2 , потери |
||||||||||||||
мощности с учетом (5.2.3), (5.2.6) и (5.2.7) равны |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
P S 2 |
|
|
|
||||
P = |
P + |
P = |
P |
+ |
|
|
|
k |
2 |
|
, |
|
(5.2.8) |
|||||
|
|
|
|
|
|
|
||||||||||||
|
x |
Ò |
|
|
|
x |
|
|
|
|
Síîì2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||

|
|
|
I |
x |
0 |
S |
íîì |
|
|
u |
0 |
0 |
S 2 |
|
|
|
|
||
Q = Q |
|
+ Q = |
|
0 |
|
|
+ |
|
k |
|
2 |
. |
(5.2.9) |
|
|||||
x |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
Ò |
|
|
100 |
|
|
100S íîì |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Если на подстанции с суммарной |
нагрузкой |
S2 |
|
работают |
параллельно k одинаковых |
||||||||||||||
трансформаторов, то их эквивалентные сопротивления в k раз меньше и равны |
rÒ |
, |
õÒ |
,а |
|||||||||||||||
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
k |
||
проводимости в k раз больше, т.е. равны kgÒ , kbÒ . Если учесть это в выражениях (5.2.1), (5.2.3), (5.2.6), (5.2.7), то получим следующие выражения для потерь мощности:
|
|
|
|
|
|
|
1 |
|
|
P S 2 |
|
|
|
|
|||||
P = k P |
|
+ |
|
|
|
|
|
k |
2 |
, |
|
|
(5.2.10) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
x |
|
|
k |
Síîì2 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
kI |
x |
0 |
S |
íîì |
|
|
|
|
1 u |
k |
0 |
S 2 |
|
|||||
Q = |
|
0 |
|
|
+ |
|
|
|
|
0 |
2 |
, |
(5.2.11) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
100 |
|
|
|
|
|
|
|
k 100Síîì |
|
|||||||
Эти же выражения можно получить и другим способом. Если подставить в (5.2.8), (5.2.9) вместо S2 поток мощности, текущей через каждый трансформатор и равной
S2 / k , то получим потери мощности в одном трансформаторе. Умножим их на k и получим выражения (5.2.10), (5.2.11) для потерь мощности в k параллельно работающих трансформаторах.
Трехобмоточные трансформаторы и автотрансформаторы. Во многих случаях на подстанции нужны три номинальных напряжения - высшее U â , среднее U c и низшее U í . Для этого можно было бы использовать два двухобмоточных трансформатора (рис. 5.2.3, а). Более экономично, чем два двухобмоточных, применять один трехобмоточный трансформатор (рис. 5.2.3, б), все три обмотки которого имеют магнитную связь (рис. 5.2.4, а). Еще более экономично применение трехобмоточных автотрансформаторов, условное обозначение которых в схемах электрических сетей приведено на рис. 5.2.3, в. Схема соединения обмоток автотрансформатора показана на рис. 5.2.4, б. Обмотка низшего напряжения магнитно связана с двумя другими. Обмотки же последовательная и общая (П и О на рис. 5.2.4, б) непосредственно электрически соединены друг с другом и, кроме того, имеют магнитную связь. По последовательной обмотке течет ток Iâ , а по общей - ( I â − I ñ ). Номинальной мощностью
автотрансформатора называют мощность, которую автотрансформатор может принять из сети высшего напряжения или передать в эту сеть при номинальных условиях работы:
|
|
|
|
Síîì = 3U â.íîì I â.íîì |
(5.2.12) |
||
Рис. 5.2.3. Схемы подстанций с тремя номинальными напряжениями:
а - два двухобмоточных трансформатора; б-трехобмоточный трансформатор; в- автотрансформатор
Эта мощность также называется проходной. Она равна предельной мощности, которую

автотрансформатор может передать из сети высшего напряжения в сеть среднего напряжения
инаоборот при отсутствии нагрузки на обмотке низшего напряжения. Последовательная обмотка П рассчитывается на типовую мощность (рис. 5.2.4,б)
|
|
|
|
= |
|
U âíîì I âíîì (1 − |
U ñíîì |
|
|
|
|
Sòèï = |
3(U â.íîì |
− U c.íîì )Iâ.íîì |
3 |
) = αSíîì |
. |
(5.2.13) |
|
||||
|
|
||||||||||
|
|
|
|
|
|
U âíîì |
|
|
|
|
|
где α = 1 − U ñ.íîì |
/ U â.íîì |
- коэффициент выгодности, показывающий, во сколько раз |
Sòèï |
||||||||
меньше Síîì . |
|
|
|
|
|
|
|
|
|
|
|
Напряжение общей обмотки меньше U â.íîì , ток в ней |
равен |
I â.íîì |
− I ñ.íîì , поэтому ее |
||||||||
мощность меньше Síîì |
. Можно показать, что мощность |
общей |
обмотки равна типовой. |
||||||||
Обмотка низшего напряжения также рассчитывается на Sòèï |
или на мощность меньше Sòèï |
. Ее |
|||||||||
номинальная мощность выражается через номинальную мощность автотрансформатора так:
Sí .íîì = α í .í Síîì , |
(5.2.13а) |
где для U â.íîì ≤ 330 кВ α í .í = 0,25; 0,4; 0,5.
Втрехобмоточном трансформаторе все три обмотки имеют мощность Síîì . В
автотрансформаторе общая и последовательная обмотки рассчитаны на типовую мощность < Síîì , а обмотки низшего напряжения - на < Síîì . Таким образом, через понижающий автотрансформатор можно передать мощность, большую той, на которую выполняются его обмотки. Чем меньше коэффициент выгодности α = Sòèï / Síîì , тем более
экономичен автотрансформатор по сравнению с трехобмоточным трансформатором. Чем ближе
номинальные напряжения на средней и высшей сторонах автотрансформатора, тем меньше
α и тем выгоднее использовать автотрансформатор. При U ñ = U âα = 0 .
Схема замещения трехобмоточного трансформатора и автотрансформатора с U íîì >220кВ приведена на рис. 5.2.4,в, а с U â.íîì ≤ 220 кВ-на рис. 5.2.4, г. Как и для двухобмоточкого трансформатора, в такой схеме замещения отсутствуют трансформации, т.е. идеальные трансформаторы, но сопротивления обмоток низшего и среднего напряжений приводят к высшему напряжению. Такое приведение соответствует умножению на квадрат коэффициента трансформации.
Потери холостого хода Px и Qx определяются так же, как и для двухобмоточного трансформатора. Потери Px - известная каталожная величина, а Qx определяются из выражения (5.2.3) по каталожному значению I x , %. Для трехобмоточных трансформаторов и автотрансформаторов задаются три значения потерь короткого замыкания по парам обмоток
|
Pê (â.í ) , Pê (â.ñ) , |
|
Pê (ñ.í ) |
и три напряжения короткого замыкания по парам обмоток uê (â.í ) %, |
|||||||||
u |
ê (â.ñ) |
0 |
, u |
|
0 |
0 |
. Каждое из каталожных значений |
P |
и u |
0 |
0 |
относится к одному из трех |
|
|
0 |
|
ê (ñ.í ) |
|
|
ê |
|
ê |
|
||||
возможных |
опытов |
короткого замыкания. Значения |
|
Pê (â.í ) |
и uê (â.í ) %, определяются при |
||||||||
замыкании накоротко обмотки низшего напряжения при разомкнутой обмотке среднего напряжения и подведении к обмотке высшего напряжения такого напряжения u ( . ) , чтобы ток в обмотке низшего напряжения трансформатора был равен номинальному. Схема этого опыта КЗ приведена на рис.5.2.4, д. Ненагруженная обмотка среднего напряжения изображена штрихами, чтобы подчеркнуть, что ток в ней равен нулю. Аналогично опыту КЗ для двухобмоточного трансформатора [см. рис. 5.2.2, г и выражение (5.2.5)] из данного опыта КЗ можно определить сумму сопротивлений обмоток высшего и низшего напряжений:
r |
+ r |
= P |
U 2 |
/ S 2 . |
(5.2.14) |
Ò. |
Ò.Í |
ê (â.í ) |
íîì |
íîì |
|
Соответственно для опытов КЗ по другим обмоткам справедливы аналогичные выражения:
r |
+ r |
= |
P |
U 2 |
|
/ S 2 |
, |
(5.2.15) |
|
Ò. |
Ò.Ñ |
|
ê ( |
â.ñ) |
íîì |
|
íîì |
|
|
r |
+ r |
= |
P |
|
U |
2 |
S 2 . |
(5.2.16) |
|
Ò.Ñ |
Ò.Í |
|
ê (ñ.í ) |
|
íîì |
íîì |
|
|
|
В уравнениях (5.2.14)-( 5.2.16) три неизвестных - активные сопротивления обмоток трансформатора rÒ. , rÒ.Ñ , rÒ.Í . Решив эти три уравнения с тремя неизвестными, получим выражения, аналогичные (5.2.5):
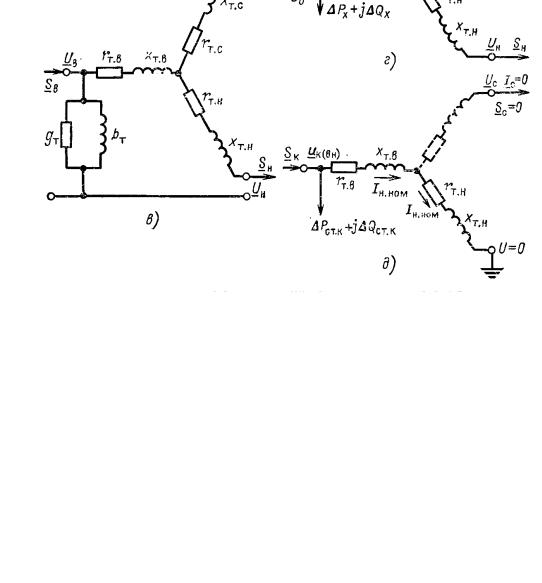
Рис. 5.2.4. Трехобмоточный трансформатор и автотрансформатор а, б - схемы соединения обмоток; в, г - Г-образная и упрощенная схемы замещения; д - схема
опыта КЗ (ВН)
|
|
|
|
P U 2 |
|
|
|
|
|||
r |
= |
|
ê.â |
|
íîì |
|
, |
|
(5.2.17) |
||
|
|
|
|
|
|
||||||
Ò. |
|
|
|
Síîì2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
P U 2 |
|
|
|
|
|||
r |
= |
|
ê.ñ |
|
íîì |
|
, |
|
(5.2.18) |
||
|
|
|
|
|
|
|
|||||
Ò.Ñ |
|
|
|
Síîì2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
U 2 |
|
|
|
|
||
r |
= |
ê.í |
|
íîì |
. |
|
(5.2.19) |
||||
|
|
|
|
|
|||||||
Ò.Í |
|
|
|
Síîì2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
В (5.2.17) - (5.2.19) величины Pê.â , |
|
Pê.ñ , |
|
Pê.í , соответствующие лучам схемы замещения, |
|||||||
определяются по каталожным значениям потерь КЗ для пар обмоток: |
|
||||||||||
Pê.â = 0,5( |
Pê (â.í ) + |
Pê (â.ñ) − |
Pê (ñ.í ) ) , |
(5.2.20) |
|||||||
Pê.ñ = 0,5( |
Pê (â.ñ) + |
|
Pê (ñ.í ) − |
Pê (â.í ) ) , |
(5.2.21) |
||||||
Pê.í = 0,5( |
Pê (â.í ) + |
|
Pê (ñ.í ) − |
Pê (â.ñ) ) . |
(5.2.22) |
||||||
Аналогично этому |
по каталожным значениям напряжении КЗ |
для пар обмоток |
uê (â.í ) %, uê (â.ñ) %, uê (ñ.í ) % |
определяются напряжения КЗ для лучей |
схемы замещения |
uê.â %, uê.ñ %, uê.í % : |
|
|
|
uê.â % = 0,5[uê (â.í ) % + uê (â.ñ) % − uê (ñ.í ) %], |
(5.2.23) |
|
uê.ñ % = 0,5[uê (â.ñ) % + uê (ñ.í ) % − uê (â.í ) %], |
(5.2.24) |
|
uê.í % = 0,5[uê (â.í ) % + uê (ñ.í ) % − uê (â.ñ) %]. |
(5.2.25) |
По найденным значениям uê.â %, uê.ñ %, uê.í % определяются реактивные сопротивления обмоток õÒ. , õÒ.Ñ , õÒ.Í по выражениям, аналогичным (5.2.6) для двухобмоточного трансформатора. Реактивное сопротивление одного из лучей схемы замещения трехобмоточного трансформатора (обычно среднего напряжения) близко к нулю.
Все современные трехобмоточные трансформаторы выпускаются с одинаковыми номинальными мощностями обмоток. Для ранее выпускавшихся трансформаторов, имеющих различные мощности отдельных обмоток, каталожные значения uê % , Pê для пар обмоток должны быть приведены к одной мощности (обычно к мощности обмотки высшего напряжения). Приведение uê % производится пропорционально отношению мощностей обмоток, а приведение
Pê - пропорционально квадрату этого отношения.
Для автотрансформаторов дополнительно указывается номинальная мощность обмотки низшего напряжения в долях номинальной мощности автотрансформатора, т. е. α í .í
(5.2.13а). Значения uê % для пар обмоток приведены к напряжению обмотки ВН и отнесены к
S |
íîì |
. Значения P |
отнесены к номинальной мощности автотрансформатора S |
íîì |
, а |
P í |
|||
|
|
ê (â.ñ) |
|
|
|
|
ê ( â.í ) |
||
и |
|
P í |
к номинальной мощности обмотки низшего напряжения, т. е. к α |
í .í |
S |
íîì |
. Эта осо- |
||
|
|
ê (ñ.í ) |
|
|
|
|
|
||
бенность записи параметров определяется условиями опыта КЗ автотрансформаторов. Например, при КЗ (ВН) напряжение на обмотке ВН поднимается до такого значения, при котором в закороченной обмотке низшего напряжения, рассчитанной на S í .íîì [см. (5.2.13а)], ток будет соответствовать не Síîì , а S í .íîì . При КЗ (ВС) ток в последовательной обмотке (рис.5.2.4,6) поднимается до
