
- •Программа, методические указания,
- •Предисловие
- •Программа курса «математика»
- •I. Введение
- •II. Математический анализ
- •III. Теория вероятностей и математическая статистика
- •Контрольные задания Задание 1.
- •Задание 2.
- •Задание 3.
- •Задание 4.
- •Задание 5.
- •Задание 6.
- •Задание 7.
- •Задание 8.
- •Задание 9.
- •Задание 10.
- •Задание 11.
- •Задание 12.
- •Задание 13.
- •Образец выполнения контрольной работы
- •Задание 4.
- •Задание 7.
- •Решение.
- •Задача 8.
- •Задача 9.
- •Задача 10.
- •Задача 11.
- •Задача 12.
- •0,17547
- •Тесты по математике
- •Список вопросов для сессионного контроля
- •Рекомендуемая литература
- •Содержание
- •Программа,
Задание 5.
Вычислить определенные интегралы:
В1а)
![]() б)
б)
В2
а)
![]() б)
б)![]()
В3
a)
![]() б)
б)
В4
a)
 б)
б)![]()
В5
а)
![]() б)
б)![]()
В6
а)
 б)
б)![]()
В7а) б)
б)![]()
В8а)![]() б)
б)![]()
В9
а)
![]() б)
б)
В10
а)
 ;
б)
;
б)![]()
В11
а)
![]() б)
б)![]()
В12
а)
![]() б)
б)
В13
а)
![]() б)
б)![]()
В14
а)
![]() б)
б)![]()
В15
а)
 б)
б)![]()
В16
а)
 б)
б)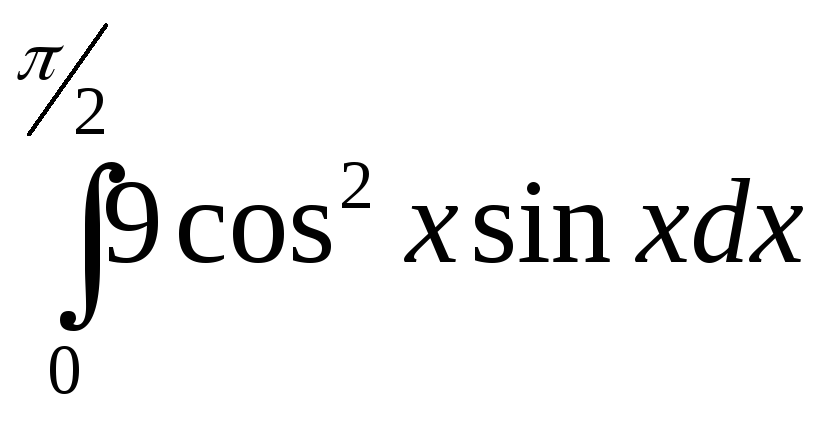
В17
а)![]() б)
б)
В18
а)
![]() б)
б)![]()
В19
а)
![]() б)
б)![]()
В20
а)
 б)
б)![]()
В21
а)
![]() б)
б)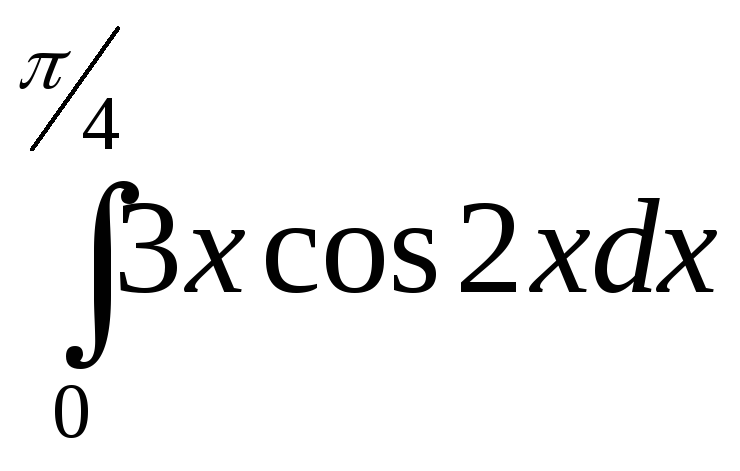
В22
а)
![]() б)
б)![]()
В23
a)
![]() б)
б)
В24
a)
 б)
б)![]()
В25
а)
![]() б)
б)![]()
В26
а)
 б)
б)![]()
В27
а)
 б)
б)![]()
В28
а)
![]() б)
б)![]()
В29
а)
![]() б)
б)
В30
а)
 ;
б)
;
б)![]()
В31
а)
![]() б)
б)![]()
В32
а)
![]() б)
б)
В33
а)
![]() б)
б)![]()
В34
а)
![]() б)
б)![]()
В35
а)
 б)
б)![]()
В36
а)
 б)
б)
В37
а)![]() б)
б)
В38
а)
![]() б)
б)![]()
В39
а)
![]() б)
б)![]()
В
40 а)
 б)
б)![]()
Задание 6.
а) Вычислить площадь фигуры, ограниченной линиями:
В
1![]() ;
;![]() .В
2.
.В
2.![]() ;
;![]() .
.
В
3.![]() ;
;![]() .В4.
.В4.![]() ;
;![]() .
.
В
5.![]() ;
;![]() .В
6.
.В
6.![]() ;
;![]() .
.
В
7.![]() ;
;![]() .В
8.
.В
8.![]() ;
;![]() .
.
В
9.![]() ;
;![]() .В10.
.В10.![]() ;
;![]() .
.
В
11.![]() ;
;![]() .В
12
.В
12![]() ;
;![]() .
.
В
13.![]() ;
;![]() .В14
.В14![]() ;
;![]() .
.
В
15.![]() ;
;![]() .В
16.
.В
16.![]() ;
;![]() .
.
В17![]() ;
;![]() .В18
.В18![]() ;
;![]() .
.
В
19![]() ;
;![]() .В 20.
.В 20.![]() ;
;![]() .
.
В
21.![]() ;
;![]() .В22
.В22![]() ;
;![]() .
.
В
23.![]() ;
;![]() .В24
.В24![]() ;
;![]() .
.
В
25.![]() ;
;![]() .В
26.
.В
26.![]() ;
;![]() .
.
В27![]() ;
;![]() .В28
.В28![]() ;
;![]() .
.
В29.![]() ;
;![]() .В
30.
.В
30.![]() ;
;![]() .
.
В
31.![]() ;
;![]() .В32.
.В32.![]() ;
;![]() .
.
В
33.![]() ;
;![]() .В 34.
.В 34.![]() ;
;![]() .
.
В
35.![]() ;
;![]() .В36
.В36 ![]() ;
;![]() .
.
В
37![]() ;
;![]() .
В 38.
.
В 38.![]() ;
;![]() .
.
В
39![]() ;
;![]() .В40
.В40![]() ;
;![]() .
.
б) Вычислить объем тела, образованного:
вращением вокруг
оси
![]() фигуры, ограниченной линиями:
фигуры, ограниченной линиями:
В
1![]() ;
;![]() .
.
В
2![]() ;
;![]() .
.
В
3.![]() ;
;![]() .
.
В
4.![]() (одна полуволна),
(одна полуволна),![]() .
.
В
5.![]() ;
;![]() ;
;![]() ;
;![]() .
.
В
6.![]() ;
;![]() .
.
В
7.![]() ;
;![]() ;
;![]() .
.
В
8.![]() ;
;![]() .
.
В
9.![]() (одна полуволна);
(одна полуволна);![]() .
.
В
10.![]() ;
;![]() ;
;![]() ;
;![]() .
.
вращением вокруг
оси
![]() фигуры, ограниченной линиями:
фигуры, ограниченной линиями:
В
11.![]() ;
;![]() .
.
В
12.![]() ;
;![]() ;
;![]() .
.
В
13.![]() ;
;![]() .
.
В
14.![]() ;
;![]() .
.
В
15.![]() ;
;![]() ;
;![]() ;
;![]() .
.
В
16![]() ;
;![]() .
.
В
17.![]() ;
;![]() ;
;![]() .
.
В
18.![]() ;
;![]() .
.
В
19.![]() ;
;![]() ;
;![]() ;
;![]() .
.
В
20.![]() ;
;![]() ;
;![]() ;
;![]() .
.
вращением вокруг
оси
![]() фигуры, ограниченной линиями:
фигуры, ограниченной линиями:
В
21.![]() ;
;![]() ;
;![]() ;
;![]() .
.
В
22.![]() (одна полуволна);
(одна полуволна);![]() .
.
В
23.![]() .
.
В
24.![]() ;
;![]() .
.
В
25.![]() ;
;![]() .
.
В
26.![]() (одна полуволна);
(одна полуволна);![]() .
.
В
27.![]() ;
;![]() .
.
В
28.![]() ;
;![]() .
.
В
29.![]() ;
;![]() .
.
В
30.![]() ;
;![]() ;
;![]() ;
;![]() .
.
вращением вокруг
оси
![]() фигуры, ограниченной линиями:
фигуры, ограниченной линиями:
В
31.![]() ;
;![]() ;
;![]() ;
;![]() .
.
В
32.![]() ;
;![]() .
.
В
33.![]() ;
;![]() .
.
В
34.![]() ;
;![]() ;
;![]() ;
;![]() .
.
В
35.![]() ;
;![]() .
.
В
36.![]() ;
;![]() .
.
В
37.![]() ;
;![]() .
.
В
38.![]() ;
;![]() .
.
В
39.![]() ;
;![]() ;
;![]() ;
;![]() .
.
В
40.![]() ;
;![]() .
.
Задание 7.
Найти общее в частное решение дифференциальных уравнений первого порядка.
В1.
2yу'
= 3х3
![]() ,
у(0)=0
,
у(0)=0
В2. 2хyy=3х5y2, у(1)=-1
В3.ysinx=ycosx,y(![]() )=0
)=0
В4. xy' = -x2y2, y(1)=1
В5.
у
=ycosx,
y(![]() )=
)=![]()
В6.yy=![]()
В7. 2yy tg 2x = sin 2x, y(0) = 0
В8.
![]() ,
у(0)= -1
,
у(0)= -1
В9. (1 + x2) y у = arctg x, y(0)= 1
В10.y'cos2xy=tg x, y(0)= -1
В11. 3x2 dy + 2xydx = 0, y(0) = 1
В12. ху arctg y= x, y(l) =0
В13.
ху![]() =х,
у(1)=0
=х,
у(1)=0
В14. y = 3x2y , y(0)= 1
В15.(1+ex)yy=e![]() ,
y(0)==0
,
y(0)==0
В16.у![]() =1+x,
у(0)=1
=1+x,
у(0)=1
В17.
![]() =tgx,
у(0)=-1
=tgx,
у(0)=-1
В18.
(2 –x2)
dy
=
![]() dx,
y(3)
= 1
dx,
y(3)
= 1
В19.
![]() у=1,
у(1)=1
у=1,
у(1)=1
В20.tgx
=yy,
y(-l)=
![]()
В21.
у'ху = 3х
![]() ,
у(0)=0
,
у(0)=0
В22.хyу=3х5 у(1)=-1
В23.ysiny=l,y(![]() )=0
)=0
В24. xy' = -x2y2, y(1)=1
В25.
yу
=cosx,
y(![]() )=
)=![]()
В26.yy=![]()
В27. y 2y tg 2x = sin 2x, y(0) = 0
В28.
![]() ,
у(0)= -1
,
у(0)= -1
В29. (1 + x2) y у = arctg x, y(0)= 1
В30.y'cosx=tg x, y(0)= -1
В31. 3x2 dy + 2xydx = 0, y(0) = 1
В32. (ху ) arctg y= x, y(l) =0
В33.
ху![]() =х,
у(1)=0
=х,
у(1)=0
В34. y = 3x2y , y(0)= 1
В35.(1+ex)yy=ey, y(0)==0
В36.у![]() =x,
у(0)=1
=x,
у(0)=1
В37. y'cos2x=tg x, y(0)= -1
В38.
(2 –x2)
dy
=
![]() dx,
y(3)
= 1
dx,
y(3)
= 1
В39.
![]() у=1,
у(1)=1
у=1,
у(1)=1
В40.tg2y
=y,
y(-l)=
![]()
Задание 8.
В1. На городскую конференцию выбирают 5 лучших врачей из 8. Сколькими способами это можно сделать?
B2. Замок сейфа открывается, если набрана правильная комбинация из 4 цифр от 0 до 9. Преступник пытается открыть сейф и набирает шифр наудачу. Найдите наибольшее возможное число безуспешных попыток, если все цифры шифра разные.
B3. В терапевтическом отделении 20 человек госпитализированы с диагнозом – пневмония и 15 – с диагнозом бронхит. Сколькими способами можно выбрать 3 пациентов на обследование?
B4. Сколькими способами можно разложить 5 упаковок аспирина в 5 шкафчиках?
B5. На приёме у терапевта 18 человек, в день терапевт осматривает 15 человек. Сколькими способами можно составить очередь к врачу?
B6. В группе 30 студентов. Сколькими способами можно выбрать шесть делегатов для переговоров с администрацией института по вопросу о свободной продаже пива в студенческом буфете?
B7. Сколькими способами можно выбрать 4 из 20 больных на уколы?
B8. В полуфинале первенства по шахматам участвует 20 студентов, а в финал выходят лишь трое. Сколько различных комбинаций по три студента можно получить в данном случае?
B9. Имеется 8 штаммов бактерий, для определения скорости их роста необходимо выбрать 4. Сколькими способами это можно сделать?
B10. Сколькими способами можно сделать больному инъекцию от трёх разных болезней, если имеются 3 шприца с различной вакциной?
B11. Сколькими способами можно разместить 4 скальпеля разной величины на хирургическом столе?
B12. Сколько слов можно составить их букв в слове “ПУЛЬМАНОЛОГ”?
B13. Сколькими способами можно выбрать 3-ёх медсестёр и одного санитара из группы, состоящей из 8 медсестёр и 3–ёх санитаров?
B14. Сколькими способами можно выбрать 5 из 20 больных на уколы?
B15. Главврач из 5 человек выбирает секретаря и методиста. Сколько способов данного выбора существует?
B16. Сколькими способами можно переставить буквы в слове “ТЕРАПЕВТ”, чтобы получить различные сочетания букв?
B17. В палате лежат 9 больных. Трём из них надо сделать УЗИ. Сколькими способами можно выбрать этих трёх?
B18. В полуфинале первенства по шахматам участвует 20 студентов, а в финал выходят лишь трое. Сколько различных комбинаций по три студента (шахматиста) можно получить в данном случае?
B19. Сколькими способами можно выбрать трёх больных из десяти на вакцинацию?
B20. Комиссия выбирает из 8 человек главврача и его заместителя. Сколькими способами это можно сделать?
В21. На городскую конференцию выбирают 5 лучших врачей из 8. Сколькими способами это можно сделать?
B22. Сколькими способами можно разместить 6–х больных на 6–ти койках в одной палате?
B23. В терапевтическом отделении 20 человек госпитализированы с диагнозом – пневмония и 15 – с диагнозом бронхит. Сколькими способами можно выбрать 3 –ёх на обследование?
B24. Сколькими способами можно разложить 5 упаковок аспирина в 5 шкафчиках?
B25. На приёме у терапевта 18 человек, в день терапевт осматривает 15 человек. Сколькими способами можно составить очередь на приём к врачу?
B26. Сколько существует способов размещения 4-ёх больных в четырёхместной палате?
B27. Сколькими способами можно выбрать 4 больных из 20 на операцию первыми?
B28. Сколькими способами можно выбрать из 10 пациентов 4 –ёх в четырёхместную палату?
B29. Имеется 6 штаммов бактерий. Для определения скорости их роста необходимо выбрать 3 штамма. Сколькими способами это можно сделать?
B30. Сколькими способами можно сделать больному инъекцию от трёх разных болезней, если имеются 3 шприца с различной вакциной?
B31. Какими способами можно разместить 4 скальпеля разной величины на хирургическом столе?
B32. Сколько слов можно составить их букв в слове “КАРДЕОЛОГ”?
B33. Сколькими способами можно выбрать 3-ёх медсестёр и одного санитара из группы, состоящей из 9 медсестёр и 3–ёх санитаров?
B34. Всего 4 хирурга. На операцию требуется 2. Сколькими способами их можно выбрать?
B35. Главврач из 9 человек выбирает секретаря и методиста. Сколько существует способов данного выбора?
B36. Сколькими способами можно переставить буквы в слове “УРОЛОГ”, чтобы получить различные сочетания букв?
B37. В палате лежат 7 больных. Трём из них надо сделать УЗИ. Сколькими способами можно выбрать этих трёх?
B38. Замок сейфа открывается, если набрана правильная комбинация из 4 цифр от 0 до 9. Преступник пытается открыть сейф и набирает шифр наудачу. Найдите наибольшее возможное число безуспешных попыток, если преступник ничего не знает про цифры шифра.
B39. Сколькими способами можно выбрать трёх больных из десяти на вакцинацию ?
B40. Комиссия выбирает из 8 человек главврача и его заместителя. Сколькими способами это можно сделать?
