Задача 12.

Вероятность заболевания гепатитом для жителя некоторой области в определённый период года составляет 510^-4. Найти вероятность того, что среди 10000 обследованных жителей ровно 5 окажутся заболевшими.

Решение.

Вероятность успеха в одном испытании очень мала (р=0,0005), а количество испытаний велико (n=10000). Поэтому воспользоваться формулой Бернулли для вычисления вероятности наступления ровно m=5 успехов сложно с точки зрения громоздкости вычислений. Воспользуемся асимптотической формулой Пуассона

, где =pn.

Тогда =0,000510000=5. И искомая вероятность равна

0,17547

Ответ: в 18% таких групп жителей будет ровно по 5 заболевших.

Задание 13.

Имеются 3 конверта. В первом конверте 25 контрольных работ по информатике; во втором – 10 контрольных работ по информатике и 5 контрольных работ по математике; в третьем – 15 контрольных работ по математике. Из выбранного наугад конверта вынули контрольную работу по информатике. Найти вероятность того, что контрольная работа взята из первого конверта (событие A).

Решение.

Из условия задачи, имеем: – событие, выбор первого конверта;– событие, выбор второго конверта;– событие, выбор третьего конверта.Так как выбор каждого конверта равновероятен, то имеем:

.

Соответственно вероятность выбора контрольных работ из первого, второго, третьего конвертов равна: .

Тогда вероятность выбора контрольных работ из первого конверта равна:

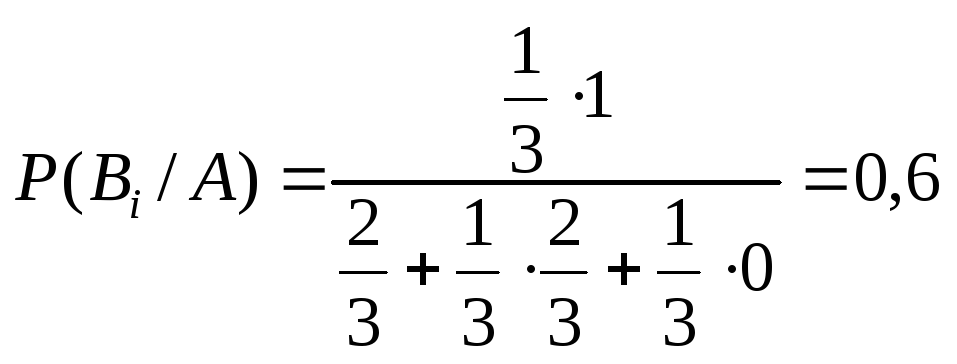
Ответ: вероятность выбора контрольной работы из первого конверта, равна 0,6.

Задание 14.

У 10 человек продолжительность инкубационного периода вирусного гепатита составила: 16, 20, 21, 15, 33, 39, 24, 24, 33, 39.

Требуется составить статистическое распределение и определить:

– математическое ожидание,

–дисперсию,

–среднеквадратическое отклонение.

Решение.

Составим статистическое распределение:

xi	15	16	20	21	24	33	39
ni	1	1	1	1	2	2	2

1. Найдем математическое ожидание по формуле:

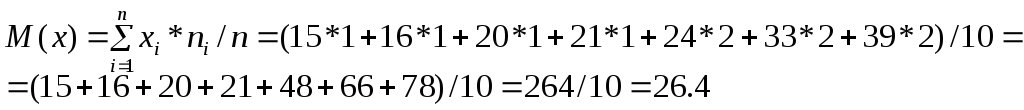
2. Найдем дисперсию СВ по формуле:

3. Найдем среднеквадратическое отклонение СВ по формуле:

Задание 15.

Налоговый инспектор, изучая зависимость выработки (ус.ед.) на одного работника от величины товарооборота магазина(ус.ед.) за отчётный период обследовал десять магазинов и получил следующие данные.

	6	11	11	7	8	10	12	6	10	9
	27	32	33	30	30	33	34	28	31	32

Полагая, что между признаками иимеет место линейная корреляционная связь, определить выборочное уравнение линейной корреляции. Построить диаграмму рассеяния и линию регрессии. Сделать вывод о направлении и тесноте связи междуи. Используя полученное уравнение линейной регрессии, оценить(ус. ед.)

Решение.

Для вычисления параметров а и b составим расчетную таблицу:

N
1	27	6	36	162	729
2	32	11	121	352	1024
3	33	11	121	363	1089
4	30	7	49	210	900
5	30	8	64	240	900
6	33	10	100	330	1089
7	34	12	14	408	1156
8	28	6	36	168	784
9	31	10	100	310	961
10	32	9	81	288	1024

Составляем систему:

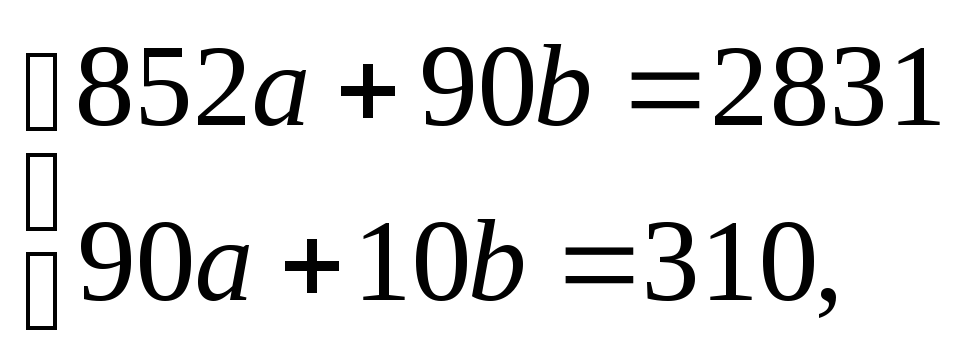
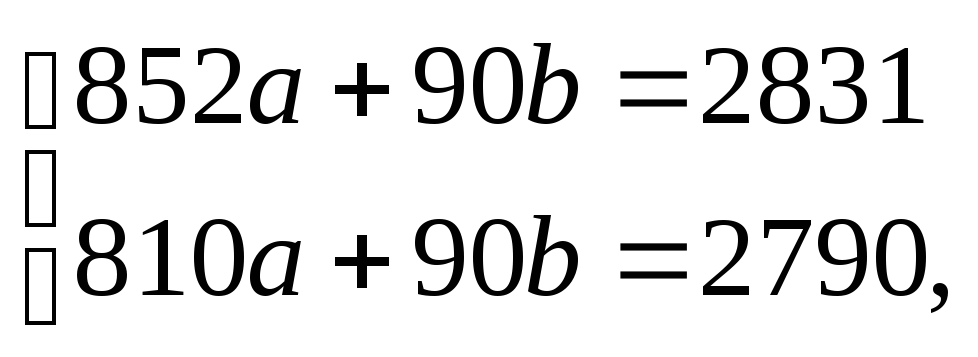
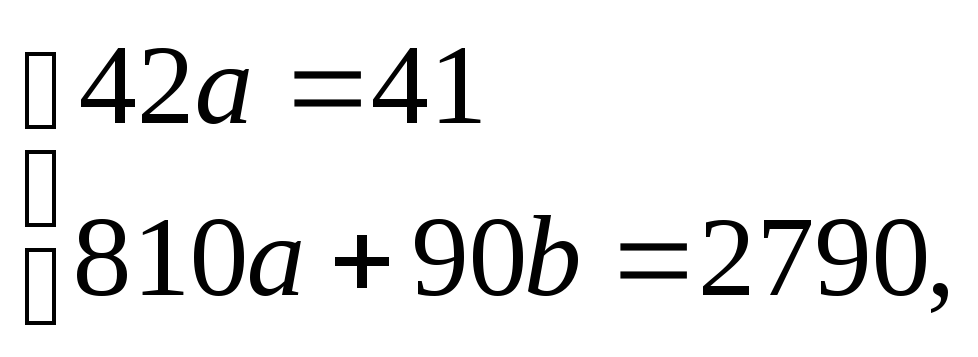
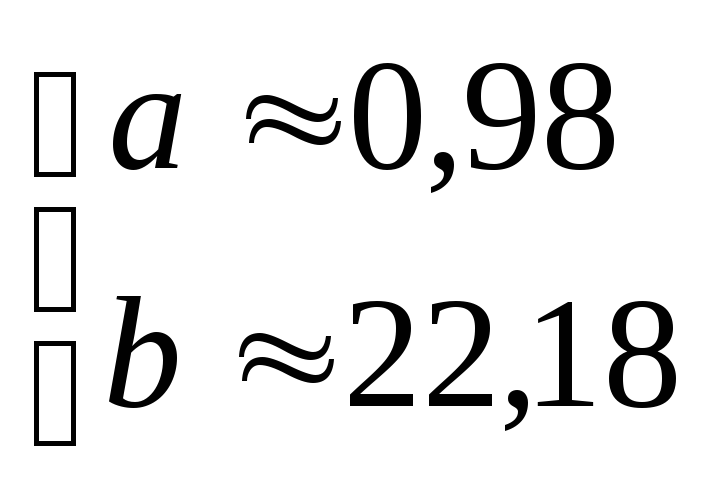
Уравнение регрессии У на Х имеет вид: .

Построим диаграмму рассеяния и линию регрессии:

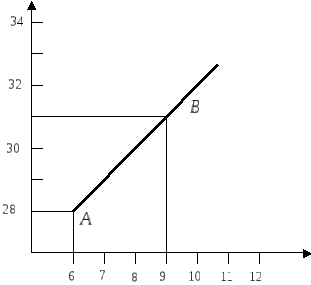
Точки инаходим из уравнения регрессии.

,

.

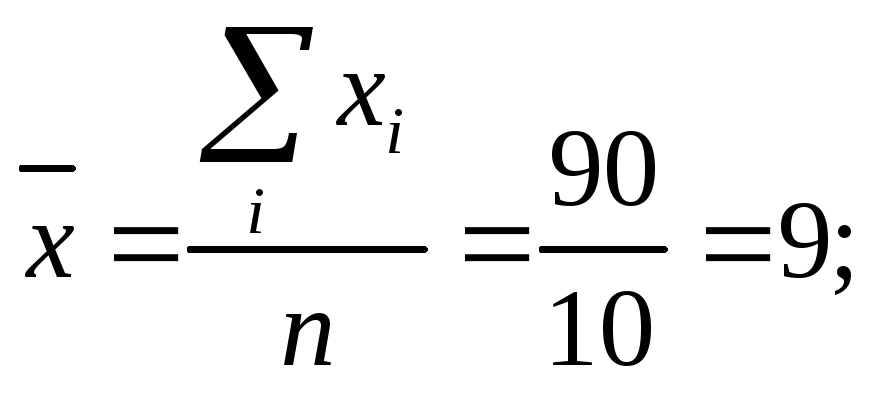
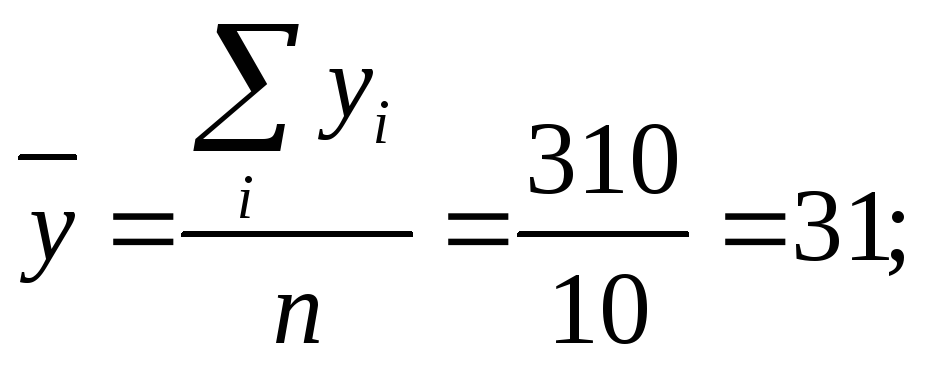
Найдем коэффициент корреляции по формуле:

.

корреляция положительная, то есть с возрастаниемХ возрастает и У. Теснота связи достаточно большая, так как 0,931.

Зная уравнение регрессии, можно вычислить предполагаемую выработки на одного работника при величине товарооборота магазина 35 ус. ед.

(ус. ед.).

Ответ: при величине товарооборота магазина 35 ус. ед. выработки на одного работника составит 56 ус. ед.