2. Коэффициенты парной корреляции найдем по формулам:

r_yx1 = Cov(x₁,y) /

r_yx2 = Cov(x₂,y) /

r_x1x2 = Cov(x₂,x1) /

(Y-Ycp)^2	X1-X1cp	(X1-X1cp)^2	X2-X2cp	(X2-X2cp)^2	(X1-X1cp)(Y-Ycp)	(X2-X2cp)(Y-Ycp)	(X1-X1cp)(X2-X2cp)
27,04000000	-13,98	195,4404	-54,7	2992,09	72,696	284,44	764,706
4,84000000	-11,58	134,0964	-42,7	1823,29	25,476	93,94	494,466
51,84000000	-7,98	63,6804	-27,7	767,29	57,456	199,44	221,046
4,84000000	-5,38	28,9444	-15,7	246,49	11,836	34,54	84,466
0,04000000	-11,38	129,5044	1,3	1,69	2,276	-0,26	-14,794
3,24000000	3,12	9,7344	10,3	106,09	5,616	18,54	32,136
1,44000000	5,72	32,7184	22,3	497,29	-6,864	-26,76	127,556
0,64000000	13,52	182,7904	29,3	858,49	10,816	23,44	396,136
23,04000000	12,22	149,3284	36,3	1317,69	58,656	174,24	443,586
116,6400000	15,72	247,1184	41,3	1705,69	169,776	446,04	649,236
233,6000000	0	1173,356000	0	10316,10000	407,7400000	1247,6000000	3198,540000
23,36000000	0	117,3356000	0	1031,610000	40,77400000	124,76000000	319,8540000
var(y)		var(X1)		var(X2)	cov(X1 Y)	cov(X2 Y)	cov(X1 X2)

r_{yx1 =} 40,774/ = 0,77881086> 0,7, то есть связь между среднедушевым потреблением овощей в месяц и среднемесячным доходом на душу населения тесная.

r_yx2 = 124,76 / = 0,80367633 > 0,7, то есть связь между среднедушевым потреблением овощей в месяц и индексом цен тесная.

r_x1x2 = 319,854 / = 0,91934626> 0,7, то есть связь между индексом цен и среднемесячным доходом на душу населения тесная.

0,77881086

Матрица парных коэффициентов примет вид: r = 0,80367633

0,91934626

2. Найдем линейные коэффициенты частной корреляции по формулам:

r_yx1*x2 = 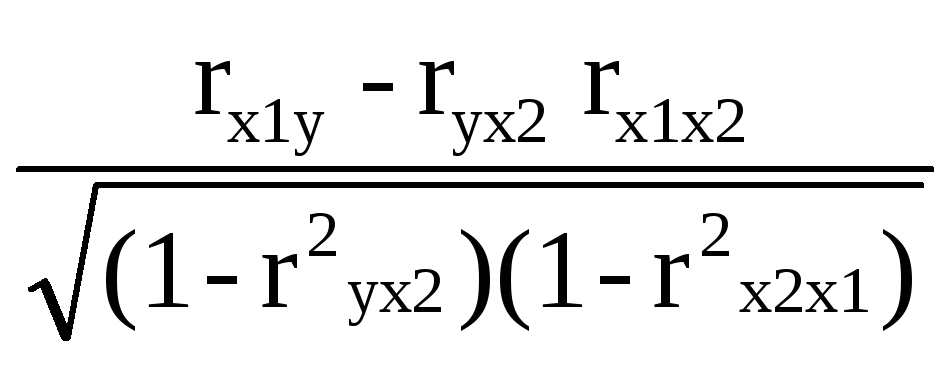= = 0,17064992<0,7, то есть связь между среднедушевым потреблением овощей в месяц и среднемесячным доходом на душу населения при исключении влияния индекса цен слабая.

r_yx2*x1 = =

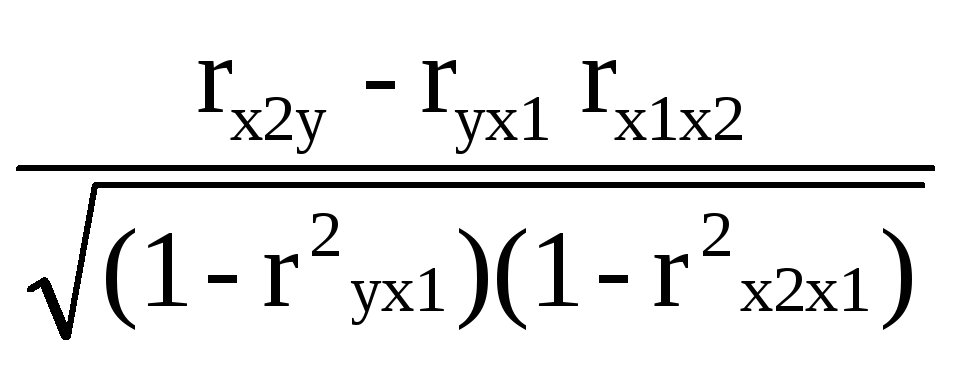= 0,35527301< 0,7, то есть связь между среднедушевым потреблением овощей в месяц и индексом цен при исключении влияния среднемесячного дохода на душу населения слабая.

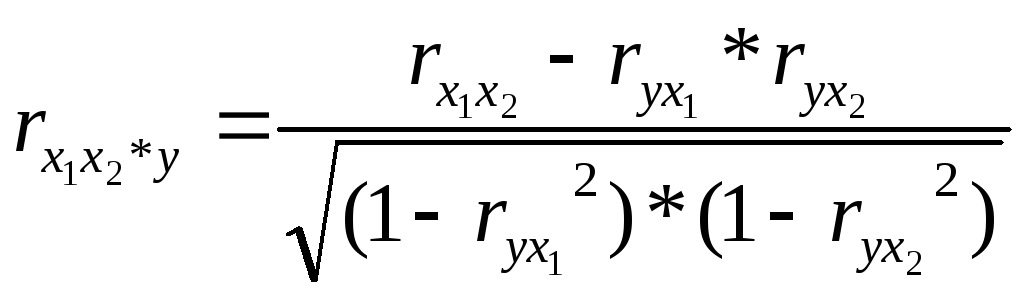
=0,810066448, значит теснота связи между факторами x₁ и x₂ при устранении влияния фактора y очень тесна.

Оценим статистическую значимость уравнения и его параметров с помощью критериев Фишера и Стьюдента.

Оценим качество уравнения:

F_факт = * = * = 6,680563929

F_табл = 4,74.

F_факт = 6,680563929 > F_табл = 4,74, следовательно, гипотеза Н_о о статистической незначимости уравнения регрессии в целом и показателя тесноты связи коэффициента корреляции отвергается. Уравнение регрессии статистически значимо и надежно.

Найдем частные значения коэффициента:

F_x1 = * = =*=0,20996423.

F_x2 = 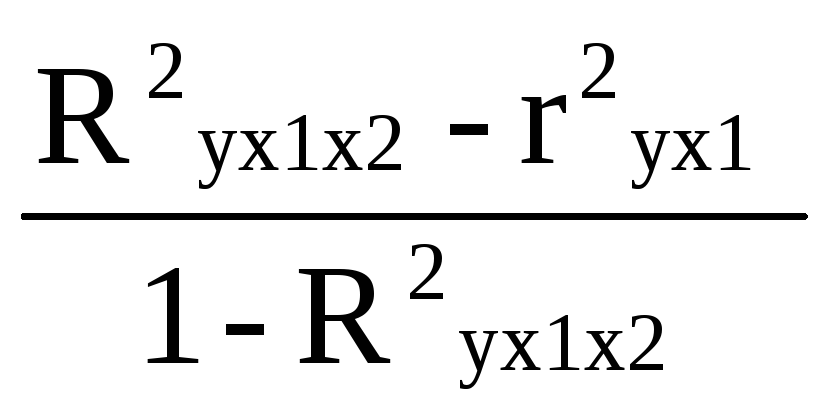* = *= 1,01115989

Т.к. F, то дополнительное включение в модель фактора х₁ после фактора х₂ статистически неоправданно и нецелесообразно и коэффициент а₁ коэффициент чистой регрессии при факторе х₁ статистически незначим.

Т.к. F, то дополнительное включение в модель фактора х₂ после фактора х₁ статистически неоправданно и нецелесообразно и коэффициент а₂ коэффициент чистой регрессии при факторе х₂ статистически незначим.

Оценим значимость коэффициентов а₁ и а₂ по критерию Стьюдента.

t_a1 = = = 0,458218536

t_a2 = = = 1,005564461

t_табл = 2,3646.

t_a1 = 0,458218536< t_табл = 2,3646 и t_a2 = 1,005564461< t_табл = 2,3646,

Гипотеза H₀ о случайной природе a₁ и а₂ принимается, эти коэффициенты статистически незначимы и ненадежны.

Найдем ошибку аппроксимации.

А = *100% = 2,900699474% < 10 %, точность модели хорошая.