
Приднестровский Государственный Университет
Имени Т.Г.Шевченко
Кафедра прикладной математики и экономико-математических методов
Индивидуальная работа №2
По дисциплине «Эконометрика»
На тему
«Модель множественной регрессии»
Выполнил
Студентка 301/02 группы
АндрияноваО.А.
Проверила
Доцент, зав.кафедрой
Спиридонова Галина Васильевна
Тирасполь 2013г.
В таблице дана информация о динамике потребления овощей за 10 лет и факторов, оказывающих влияние на объем потребления, индекс цен и среднемесячный доход. Сформировать свой вариант исходных данных по данным таблицы, используя формулы:
D`t=Dt+N;
I`t=It-0.1N;
P`t=Pt+1.5N,
Где N=1.
Требуется:
-
найти зависимость среднедушевого потребления от размера дохода и индекса цен в естественном и стандартизированном виде.
-
построить матрицу парных коэффициентов корреляции.
-
найти линейные коэффициенты частной корреляции и линейный коэффициент множественной корреляции.
-
построить трендовую модель изменения цен.
-
для трендовых моделей найдите коэффициенты автокорреляции первого порядка и дайте их интерпретацию.
-
оценить статистическую значимость уравнений и их параметров с помощью критериев Фишера и Стьюдента.
-
используя построенные трендовые модели для дохода и индекса цен, осуществить прогноз спроса на овощи на следующие 2 года (11 и 12).
-
рассчитать коэффициенты эластичности спроса на овощи в зависимости от дохода и уровня цен для 11 года.
-
построить графики трендовых моделей.
|
номер года t |
среднемесячный доход на душу населения (руб) Dt |
индекс цен в % It |
среднедушевое потребление овощей в месяц (кг) Pt |
|
1 |
15,0 |
123 |
70 |
|
2 |
17,4 |
135 |
73 |
|
3 |
21,0 |
150 |
68 |
|
4 |
23,6 |
162 |
73 |
|
5 |
17,6 |
179 |
75 |
|
6 |
32,1 |
188 |
77 |
|
7 |
34,7 |
200 |
74 |
|
8 |
42,5 |
207 |
76 |
|
9 |
41,2 |
214 |
80 |
|
10 |
44,7 |
219 |
86 |
1.Преобразуем данные согласно варианту:
|
|
Номер года, t |
Среднемесячный доход на душу населения (руб.): Dt, X1 |
Индекс цен в %,Jt ,X2 |
Среднедушевое потребление овощей в месяц (кг): P1 , Y |
|
|
1 |
16 |
122,9 |
71,5 |
|
|
2 |
18,4 |
134,9 |
74,5 |
|
|
3 |
22 |
149,9 |
69,5 |
|
|
4 |
24,6 |
161,9 |
74,5 |
|
|
5 |
18,6 |
178,9 |
76,5 |
|
|
6 |
33,1 |
187,9 |
78,5 |
|
|
7 |
35,7 |
199,9 |
75,5 |
|
|
8 |
43,5 |
206,9 |
77,5 |
|
|
9 |
42,2 |
213,9 |
81,5 |
|
|
10 |
45,7 |
218,9 |
87,5 |
|
|
Сумма |
299,8 |
1776 |
767 |
|
|
Средняя |
29,98 |
177,6 |
76,7 |
Построим линейную модель вида:
y = a1x1+a2x2+b.параметры a1,a2,b найдем, используя метод наименьших квадратов, для чего решим систему уравнений:
a 1
1![]() +
a2
+
a2![]() +
b
+
b
![]() =
=![]() ;
;
a1![]() +
a2
+
a2![]() +
b
+
b![]() =
=![]() ;
;
a1![]() +
a2
+
a2![]() +
bn =
+
bn =![]() ;
;
Найдем необходимые значения в таблице:
|
X1^2 |
X2^2 |
X1*X2 |
X1*Y |
X2*Y |
|
256,00000000 |
15104,41000000 |
1966,40000000 |
1144,00000000 |
8787,35000000 |
|
338,56000000 |
18198,01000000 |
2482,16000000 |
1370,80000000 |
10050,05000000 |
|
484,00000000 |
22470,01000000 |
3297,80000000 |
1529,00000000 |
10418,05000000 |
|
605,16000000 |
26211,61000000 |
3982,74000000 |
1832,70000000 |
12061,55000000 |
|
345,96000000 |
32005,21000000 |
3327,54000000 |
1422,90000000 |
13685,85000000 |
|
1095,61000000 |
35306,41000000 |
6219,49000000 |
2598,35000000 |
14750,15000000 |
|
1274,49000000 |
39960,01000000 |
7136,43000000 |
2695,35000000 |
15092,45000000 |
|
1892,25000000 |
42807,61000000 |
9000,15000000 |
3371,25000000 |
16034,75000000 |
|
1780,84000000 |
45753,21000000 |
9026,58000000 |
3439,30000000 |
17432,85000000 |
|
2088,49000000 |
47917,21000000 |
10003,73000000 |
3998,75000000 |
19153,75000000 |
|
10161,36 |
325733,7 |
56443,02 |
23402,4 |
137466,8 |
|
1016,136 |
32573,37 |
5644,302 |
2340,24 |
13746,68 |
|
|
|
|
|
|
Получим систему:
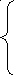
10161, 36 a1 + 56443,02 a2 + 299,8 b = 23402,4;
56443,02 а1 + 325733,7 a2 + 1776 b = 137466,8;
299,8 a1 + 1776 a2 + 10 b =767;
Решим систему методом Крамера:


10161, 36 56443,02 299,8
D = 56443,02 325733,7 1776 = 18737997
299,8 1776 10


23402,4 56443,02 299,8
D1 = 137466,8 325733,7 1776 = 2157881,1
767 1776 10


10161, 36 23402,4 299,8
D2 = 56443,02 137466,8 1776 = 1597062,46
299,8 767 10


10161, 36 56443,02 23402,4
D3 = 56443,02 325733,7 137466,8 = 1088872802
299,8 1776 767
a1 = D1/D = 2157881,1/ 18737997= 0,115160713
a2 = D2/D = 1597062,46 / 18737997= 0,085231226
b = D3/D = 1088872802/ 18737997= 58,11041605
yp = 0,115160713 x1 + 0,085231226 x2 + 58,11041605
Если среднемесячный доход на душу населения увеличится на 1 рубль, а индекс цен останется неизменным, то среднедушевое потребление овощей в месяц увеличится на 0,115160713 кг. Если индекс цен увеличится на 1%, а среднемесячный доход на душу населения останется неизменным, то среднедушевое потребление овощей в месяц увеличится на 0,085231226 кг.
Найдем коэффициенты множественной корреляции и детерминации.
Коэффициент множественной корреляции найдем по формуле:
R2yx1x2
= 1 -
![]() /
/
![]() = 0,
65620765
= 0,
65620765
R =![]() =0,810066448.
коэффициент корреляции больше 0,7, а
коэффициент детерминации меньше 0,7, это
значит, что связь между среднедушевым
потреблением овощей в месяц, индексом
цен и среднемесячным доходом на душу
населения средней тесноты.
=0,810066448.
коэффициент корреляции больше 0,7, а
коэффициент детерминации меньше 0,7, это
значит, что связь между среднедушевым
потреблением овощей в месяц, индексом
цен и среднемесячным доходом на душу
населения средней тесноты.
