GEOMETRIYa_1

ГЕОМЕТРИЯ

1. Аффинные пространства. Аффинные координаты. Формулы преобразования аффинных координат точек.

2. Плоскости в аффинных пространствах.

Плоскость определенной точкой и двумя неколлинеарными векторами называется множество точек аффинного пространства такое что .

- числа (параметры)

- векторно-параметрическое уравнение плоскости

– опорная точка

- базисные векторы плоскости

- общее уравнение плоскости

Одномерная плоскость – прямая.

Если m = n – 1, то плоскость называется гиперплоскостью.

- параметрическое уравнение n-мерной плоскости

Если ранг = 1, то плоскости совпадают.

Если ранг матрицы = 2, то плоскости пересекаются по прямой.

Плоскости называются параллельными, если либо

(ранг матрицы =1 ранг расширенной матрицы = 2)

Плоскости называются скрещивающимися, если они не параллельны и не имеют общих точек.

3. Аксиомы скалярного умноження. Евклидовые векторные пространства. Евклидовые точечно-векторные пространства.

4.Угол между векторами. Ортогональные векторы. Ортонормированные базисы и прямоугольные координаты.

5. Векторное и смешанное произведение.

6. Теория прямых на аффинной плоскости.

7.Теория прямых на евклидовой плоскости.

8. Эллипс, гипербола, парабола.

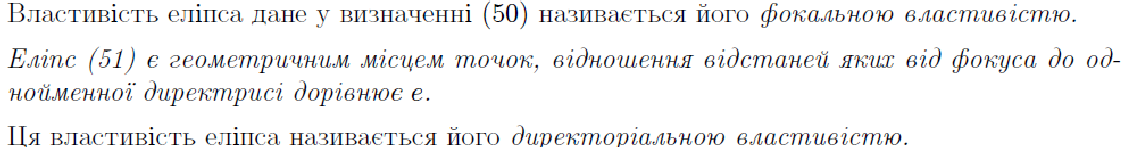
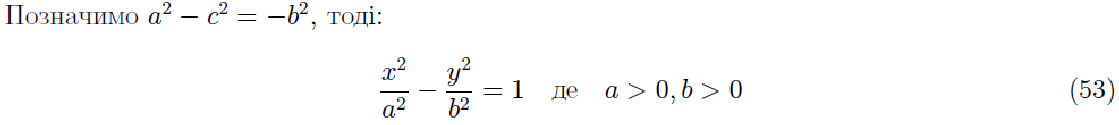
9.Площини у 3-вимірному афінному та евклідовому просторі.

Плоскость в трехмерном аффинном пространстве может быть задана:

1) векторно параметрическим уравнением , где a, b – неколлинеарные направленные векторы плоскости, - радиус-вектор фиксированной точки плоскости.

Возьмем теперь в пространстве аффинную систему координат Охyz. Пусть в этой системе координат точки и векторы имеют соответствующие координаты . Тогда в заданной системе координат уравнения равносильные трем уравнениям для координат: . Эти уравнения называются параметрическими уравнениями плоскости.

2) общим уравнением

.

Система уравнения или эквивалентна ее системе выражает линейную зависимость рядов матрицы или уравнение где Уравнение можно назвать общим уравнением плоскости, которая проходит через тоску .

Уравнением плоскости, которое проходит через три точки с координатами , которое не лежит на одной прямой, можно записать в виде

Пусть плоскость проходит через точки где . Тогда уравнение этой плоскости можно записать в виде . Это уравнение называют уравнением плоскости в отрезках.

Прямая линия в пространстве может быть задана:

1) векторно параметрическим уравнением , где а – направленный вектор прямой, - радиус-вектор фиксированной точки прямой.

Если уравнение записать в аффинной системе координат, то получим параметрическое уравнение прямой в пространстве: . Включением параметра параметрические уравнения сводится к канонической форме . Уравнение прямой, которое проходит через две разные точки, можно задать в векторной форме , где - радиус-вектор данных точек, а - их аффинные координаты.

Прямую l можно задать как линию пересечения

20. Відстань точки до прямої на площині і в просторі. Відстань між мимобіжними прямими.

15. Топологическое пространство.

Пример:

16. Визначення кривої в диференціальної геометрії. Елементарна, проста та загальна крива. Регулярна крива. Способи завдання кривих.

17. Кривина та скрут кривої. Тригранник Френе.

Фигура, составленная из касательной, главной нормали и бинормали, а также из трех плоскостей, попарно содержащих эти прямые, называют естественным трёхгранником (трёхгранником Френе

18. Формули Френе.

Фигура, составленная из касательной, главной нормали и бинормали, а также из трех плоскостей, попарно содержащих эти прямые, называют естественным трёхгранником (трёхгранником Френе)

Если рёбра естественного трёхгранника в данной точке кривой принять за оси прямоугольной декартовой системы координат, то уравнение кривой в естественной параметризации раскладывается в окрестности этой точки в ряд по координате вдоль кривой.

С помощью Френе формулы исследуются дифференциально-геометрические свойства

кривых линий.

19.Лінії на поверхні (лінії кривини, асимптотичні лінії ).