12. Визначник квадратної матриці та його властивості. Теорема Крамера.

Определителем квадратной матрицы над полем P называется число из поля P, которое обозначается , и которое равно сумме всевозможных слагаемых вида . Определитель квадратной матрицы - .

Минором элемента квадратная матрица n-го порядка называется определитель матрицы n-1 порядка, который получается из данной матрицы вычеркиванием i строки и j столбца. Обозначается .

Алгебраическим дополнением элемента квадратной матрицы А называется минор этого элемента взятый со знаком . Обозначим .

Свойства определителя n-го порядка:

1. А- квадратная матрица, тогда .

2. Если в матрице А все элементы какой-либо строки (столбца) равны нулю, то определителя обязательно содержит элементы качества сомножетеля из нулевой строки (столбца), поэтому все слагаемые определителя будет равен нулю.

3. Если матрица В получется из квадратной матрицы А транспозиции двух строк (столбов), то определитель матрицы В отличается от знаком .

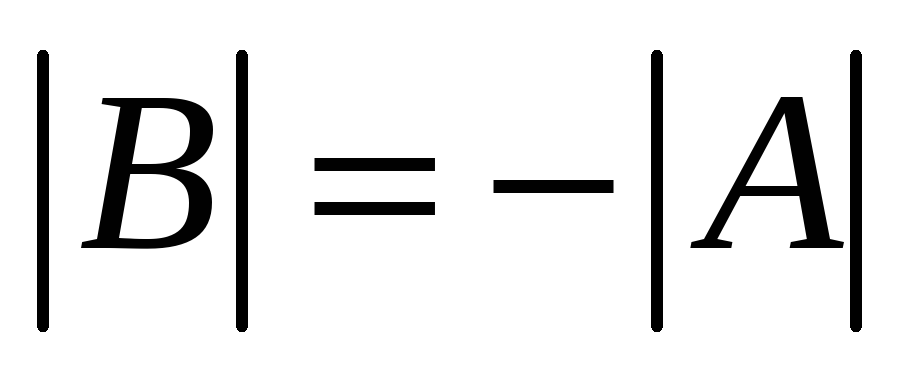4. Если в квадратной матрице А имеется две одинаковых строки (столбца), то определитель такой матрицы равен нулю.

5. Определитель квадратной матрицы равен сумме произведний элементов какой-либо строки (столбца) на их алгебраическое дополнение.

6. Сумма произведений элементов какой-либо строки квадратной матрицы на алгебраическое дополнение соответсвенных элементов другой строки (столбца) равен нулю. .

7. Если матрица В получается из квадратной матрицы А умножение всех элементов какой-либо строки (столбца) на некоторе число , то .

8. Если матрица В получается из квадратной матрицы А прибавлением ко всем элементам какой-либо строки (столбца) соответсвенно элементов других строк (столбцов), умножить на одно и тоже число , то .

9. Если в квадратной матрице А все элементы какой-либо строки представляют собой сумму двух слагаемых , где , оличается от матрицы А i-ой строкой, элементы которой представляют собой сумму двух слагаемых В матрицы , в качестве элементов i строки берется первые слагаемые i строки в матрице А, а в матрице соответственно берутся вторые слагаемые матрицы А, и аналогично, , определяются в случае, когда все элементы j столбца представляют собой сумму двух слагаемых.

Формула для вычисления обратной матрицы - , где - матрица, которая получается из матрицы А заменой каждого элемента на его алгебраическое дополение с последующим транспланирование.

Th (Крамера): Если в слу число уравнений равно числу неизвестных и определенных матрицей системы , то система имееет единственное решение , где вычисляется по формулам: , где - определителоь матрицы, которая получается из матрицы слу заменой n-го столбца столбцом свободных членов.

Док-во: Рассмотрим произвольное слу состоящее из n уравнений и зависящих от n-переменных. (1). Т.к. , что , поэтому слу имеет единственное решение (2). Система равенств (2) равносильна след. матричному равенству: (3). Т.к. определитель , то для матрицы , поэтому имеем, что , поэтому , где . Обозначим через - матрицу, которая получена из матрицы А заменой к-столбца на столбец свободных членов, и разложим определитель по элементам к столбца. . Т.к. , то имеем получим . - ■