
Тема: 10 Эллипс
Содержание: нахождение канонического уравнения эллипса, изучение его свойств по каноническому уравнению. Уравнение касательной к эллипсу, условие касания, взаимное расположение эллипса и прямой.
Цель: сформировать геометрическое представление об эллипсе, научить находить уравнение эллипса по его свойствам.
Форма контроля: опрос.
Задания:
№ 444
Составить уравнение эллипса, фокусы которого лежат на оси абсцисс, симметрично относительно начала координат, зная, кроме того, что:
-
его полуоси равны 5 и 2;
-
его большая ось равна 10, а расстояние между фокусами 2с=8;
-
его малая ось равна 24, а расстояние между фокусами 2с=10;
-
расстояние между фокусами 2с=6 и эксцентриситет е=3/5;
-
его большая ось равна 20, а эксцентриситет е=3/5;
-
его малая ось равна 10, а эксцентриситет е=12/13;
-
расстояние между его директрисами равно 5 и расстояние между фокусами 2с=4;
-
его большая ось равна 8, а расстояние между его директрисами равно 16;
-
его малая ось равна 6, а расстояние между директрисами равно 13;
-
расстояние между его директрисами равно 32 и эксцентриситет е=3/5
№ 448
Вычислить площадь четырехугольника, две вершины которого лежат в фокусах эллипса x2+5y2=20, а две другие совпадают с концами его малой оси.
№ 450
Вычислить площадь четырехугольника, две вершины которого лежат в фокусах эллипса 9x2+5y2=1.
№ 451
Вычислить
расстояние от фокуса F(c;
0)
эллипса
![]() до
односторонней с этим фокусом директрисы.
до
односторонней с этим фокусом директрисы.
№ 453
На
эллипсе
![]() найти точки, абсцисса которых равна -3.
найти точки, абсцисса которых равна -3.
№ 454
Определить какие из точек А1 (-2;3), А2 (2;-2), А3 (2;-4), А4 (-1;3), А 5(-4;-3), А6(3;-1), А7 (3;-2), А8 (2;1), А9 (0;15) и А10 (0;-16) лежат на эллипсе 8x2+5y2=77, какие внутри него, а какие вне его.
№ 456
Эксцентриситет эллипса е=2/3, Фокальный радиус точки М эллипса равен 10. Вычислить расстояние от точки М до односторонней с этим фокусом директрисы.
№ 459
Убедившись,
что точка М1(-4;
2,4)
лежит на эллипсе
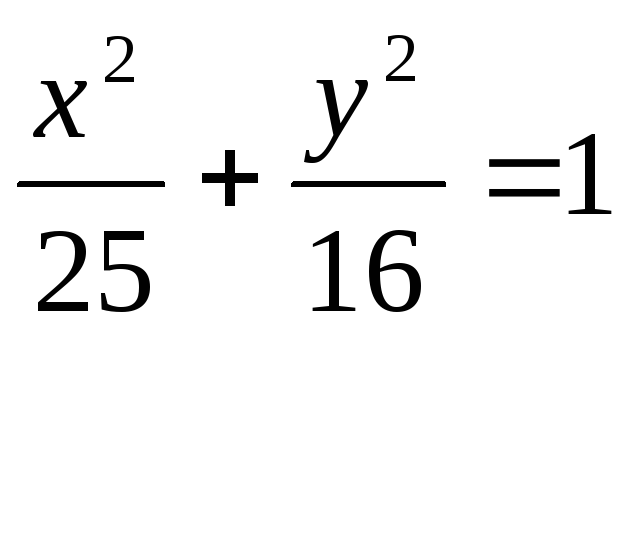 ,
определить фокальные радиусы точки М1.
,
определить фокальные радиусы точки М1.
№ 465
Составить уравнение эллипса, фокусы которого расположены на оси абсцисс, симметрично относительно начала координат, если даны:
-
точка М1(-2
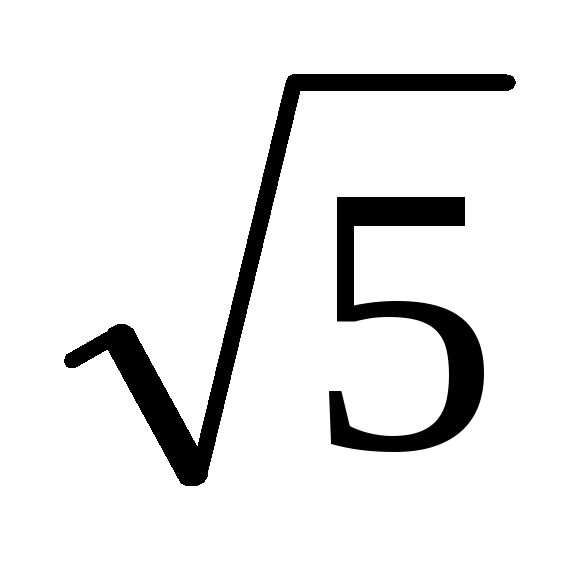 ;
2)
эллипса и его малая полуось b=3;
;
2)
эллипса и его малая полуось b=3; -
точка М1(2; -2) эллипса и его большая полуось a=4;
-
точка М1(4;-
 )
и М2(2
)
и М2(2 ;
3)
эллипса;
;
3)
эллипса; -
точка М1(
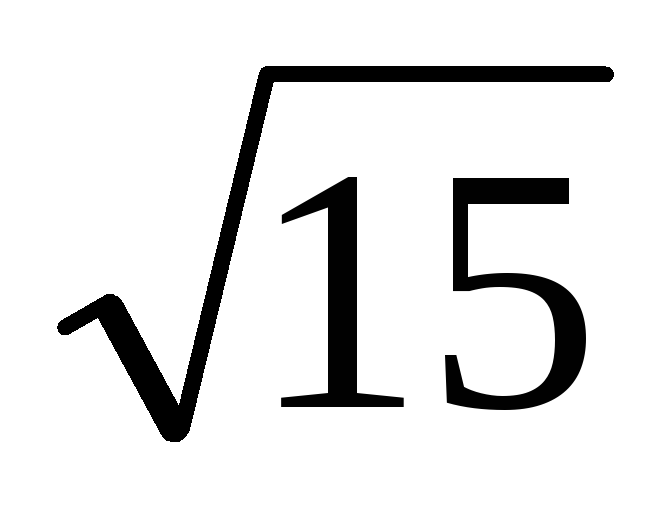 ;
-1)
эллипса и расстояние между фокусами
2с=8;
;
-1)
эллипса и расстояние между фокусами
2с=8; -
точка М1(2; -5/3) эллипса и его эксцентриситет е=2/3;
-
точка М1(8; 12) эллипса и расстояние r1=20 от нее до левого фокуса;
-
точка М1(-
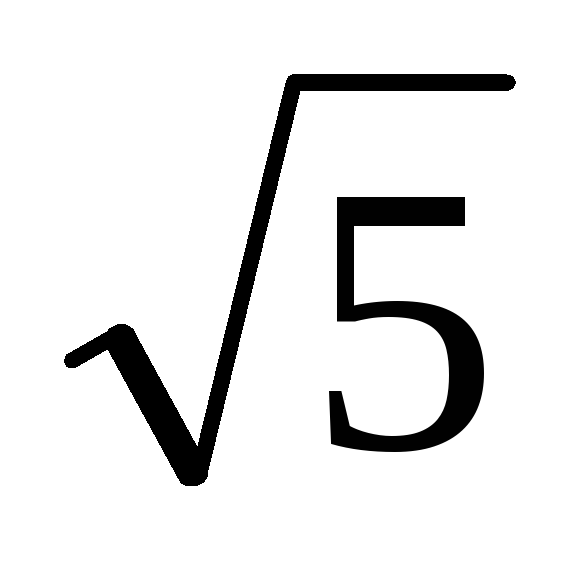 ;
2)
эллипса и расстояние между его
директрисами равно 10.
;
2)
эллипса и расстояние между его
директрисами равно 10.
№ 483
Определить, как расположена прямая относительно эллипса: пересекает, касается или проходит вне его, если прямая и эллипс заданы следующими уравнениями:
-
2x - y - 3 =0
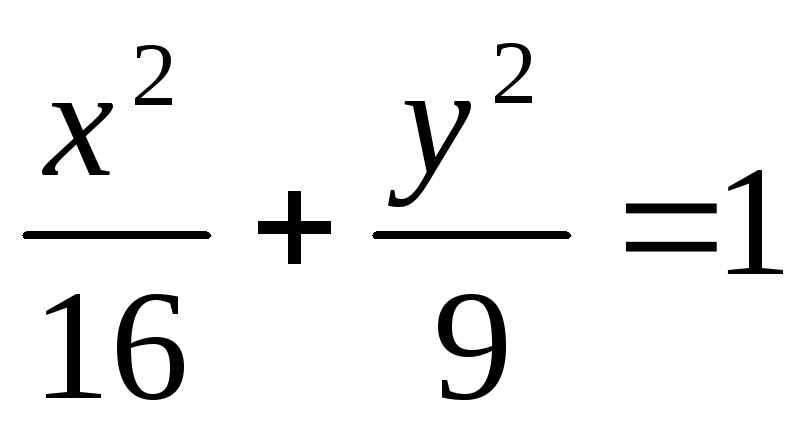
-
2x+ y -10=0
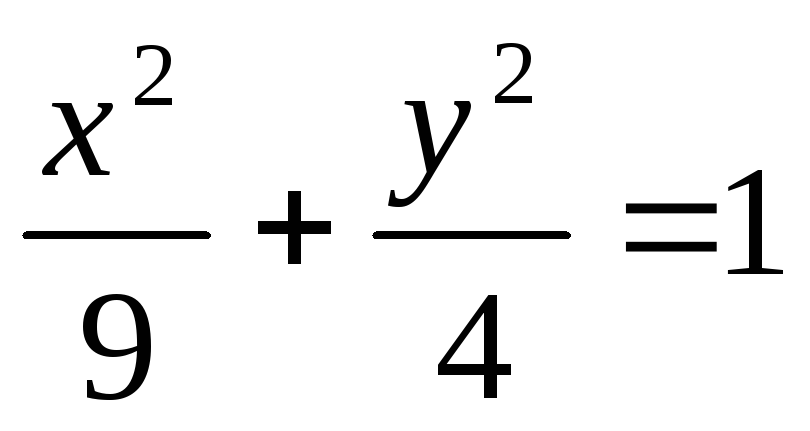
-
3x+2y-20=0
![]()
№ 484
Определить при каких значениях m прямая y= - x + m
-
пересекает эллипс
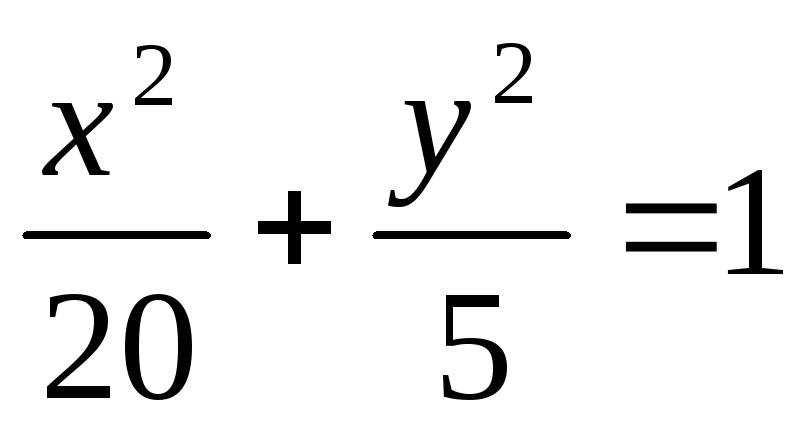 ;
; -
касается его;
-
проходит вне этого эллипса.
№ 487
Доказать,
что касательные к эллипсу
![]() ,
проведенные в концах одного и того же
диаметра, параллельны (Диаметром эллипса
называется его хорда, проходящая через
центр).
,
проведенные в концах одного и того же
диаметра, параллельны (Диаметром эллипса
называется его хорда, проходящая через
центр).
№ 488
Составить
уравнения касательных к эллипсу
![]() ,
параллельных прямой 3x+2y+7=0.
,
параллельных прямой 3x+2y+7=0.
№ 489
Составить уравнения касательных к эллипсу x2+4y2=20, перпендикулярных к прямой 2x-2y-13=0.
№ 490
Провести
касательные к эллипсу
![]() параллельно прямой 4x-2y+23=0
и вычислить расстояние d
между ними.
параллельно прямой 4x-2y+23=0
и вычислить расстояние d
между ними.
№ 491
На
эллипсе
![]() найти точку М1,
ближайшую к прямой 2x-3y+25=0,
и вычислить расстояние d
от
точки М1
до этой прямой.
найти точку М1,
ближайшую к прямой 2x-3y+25=0,
и вычислить расстояние d
от
точки М1
до этой прямой.
№ 492
Из
точки А(10/3;
5/3)
проведены касательные к эллипсу
![]() .
Составить
их уравнения.
.
Составить
их уравнения.
№ 493
Из
точки С(10;
-8)
проведены касательные к эллипсу
![]() .
Составить уравнение хорды, соединяющей
точки касания.
.
Составить уравнение хорды, соединяющей
точки касания.
№ 497
Доказать, что произведение расстояний от центра эллипса до точки пересечения любой его касательной с фокальной осью и до основания перпендикуляра, опущенного из точки касания на фокальную ось, есть величина постоянная, равная квадрату большой полуоси эллипса.
№ 498
Доказать, что произведение расстояний от фокуса до любой касательной к эллипсу равно квадрату малой полуоси.
№ 499
Прямая x-y-5=0 касается эллипса, фокусы которого находятся в точках F1(-3; 0) и F2(3; 0). Составить уравнение эллипса.
Тема: 11 Гипербола. Парабола.
Содержание: нахождение канонических уравнений гиперболы, параболы; исследование их свойств, условия касания, касательная к гиперболе и параболе.
Цель: формирование геометрического представления о гиперболе и параболе, научить определять свойства кривых по их уравнениям и находить уравнения кривых по их свойствам.
Форма контроля: опрос, самостоятельная работа (40 мин, 3 задания, пакет заданий «D»)
Задания:
№ 515
Составить уравнение гиперболы, фокусы которой расположены на оси абсцисс симметрично относительно начала координат, зная, кроме того, что:
-
ее оси 2a=10 и 2b=8;
-
расстояние между фокусами 2с=10 и ось 2b=8;
-
расстояние между фокусами 2с=6 и эксцентриситет е=3/2;
-
ось 2а=16 и эксцентриситет е=5/4;
-
уравнения асимптот
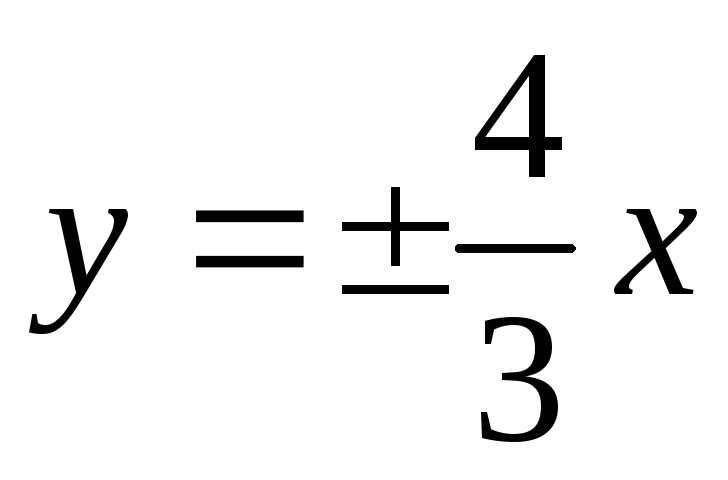 и расстояние между фокусами 2с=20;
и расстояние между фокусами 2с=20; -
расстояние между директрисами
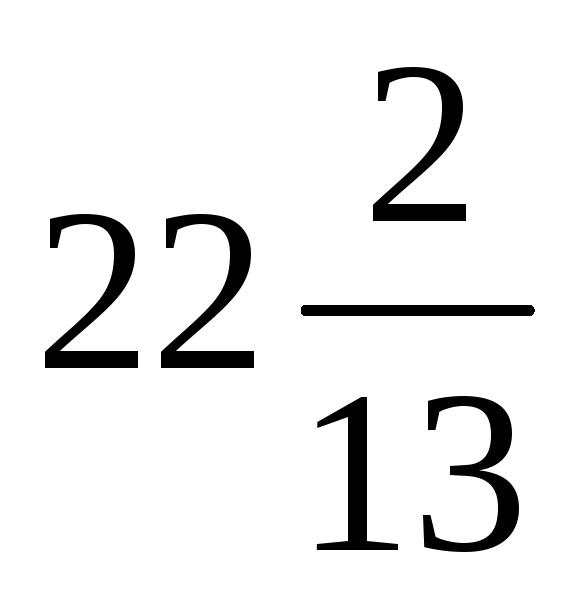 и расстояние между фокусами 2с=26;
и расстояние между фокусами 2с=26; -
расстояние между директрисами равно 35/2 и ось 2b=6;
-
расстояние между директрисами равно 8/3 и эксцентриситет е=3/2;
-
уравнения асимптот
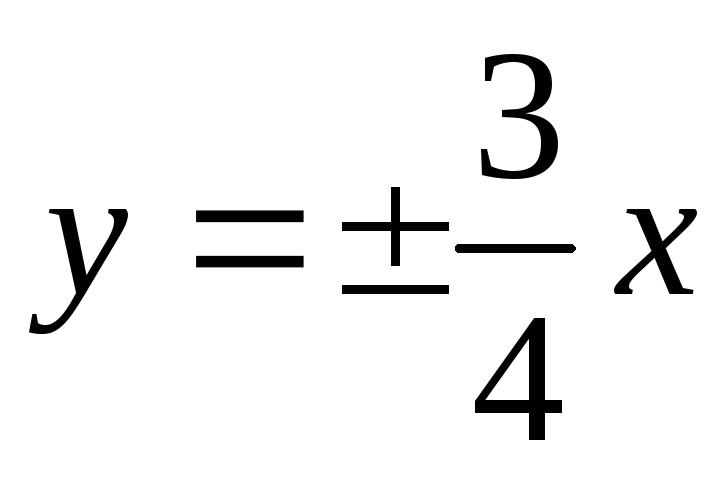 и расстояние между директрисами
и расстояние между директрисами
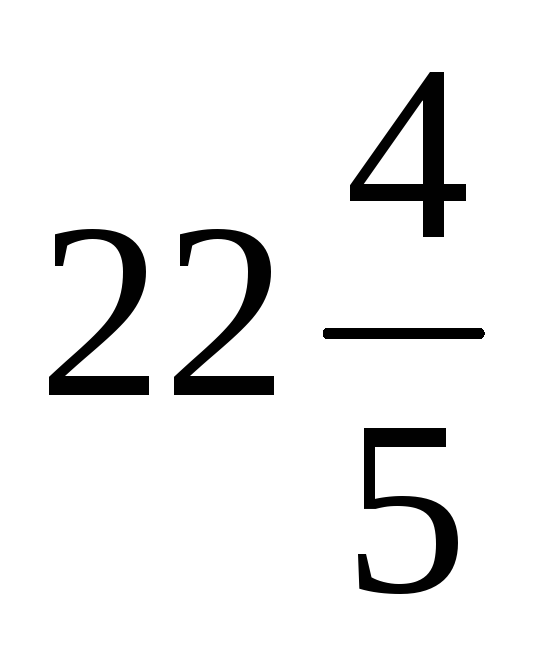 .
.
№ 518
Дана гипербола 16x2-9y2=144.Найти:
-
полуоси а и b;
-
эксцентриситет;
-
уравнения асимптот;
-
уравнения директрис.
№ 520
Вычислить
площадь треугольника, образованного
асимптотами гиперболы
![]() и прямой 9x+2y-24=0.
и прямой 9x+2y-24=0.
№ 524
Эксцентриситет гиперболы е =2, фокальный радиус ее точки М, проведенный из некоторого фокуса, равен 16. Вычислить расстояние от точки М до односторонней с этим фокусом директрисы.
№ 528
Определить
точки гиперболы
![]() ,
расстояние которых до правого фокуса
равно 4,5.
,
расстояние которых до правого фокуса
равно 4,5.
№ 530
Через
левый фокус гиперболы
![]() проведен перпендикуляр к ее оси,
содержащей вершины. Определить расстояния
от фокусов до точек пересечения этого
перпендикуляра с гиперболой.
проведен перпендикуляр к ее оси,
содержащей вершины. Определить расстояния
от фокусов до точек пересечения этого
перпендикуляра с гиперболой.
№ 532
Составить уравнение гиперболы, фокусы которой лежат на оси абсцисс, симметрично относительно начала координат, если даны:
-
точки М1(6; -1) и М2(-8;
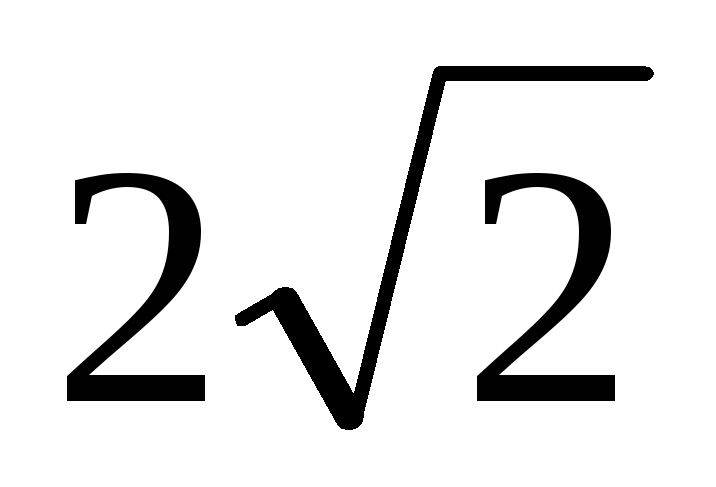 )
гиперболы;
)
гиперболы; -
точка М1(-5; 3) гиперболы и эксцентриситет е=
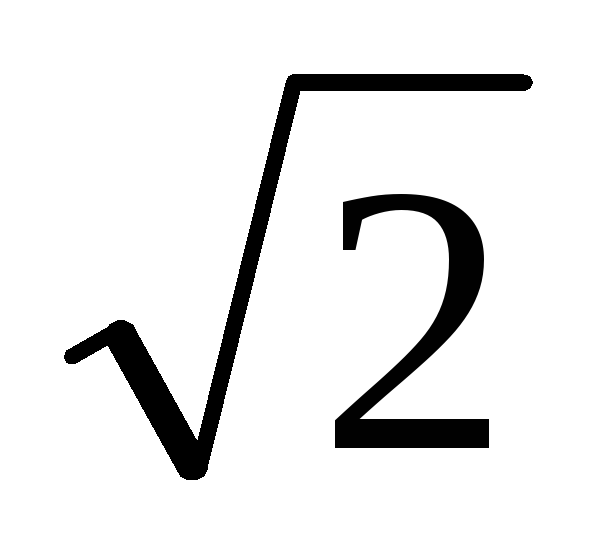 ;
; -
точка М1(9/2; -1) гиперболы и уравнения асимптот
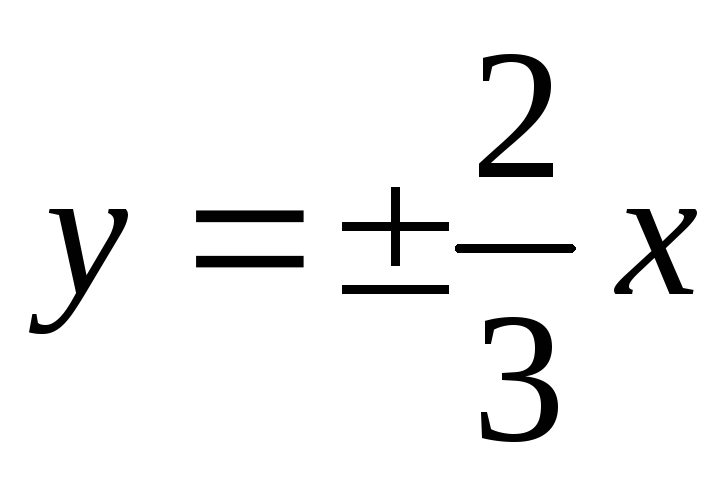 ;
; -
точка М1(-3; 5/2) гиперболы и уравнения директрис
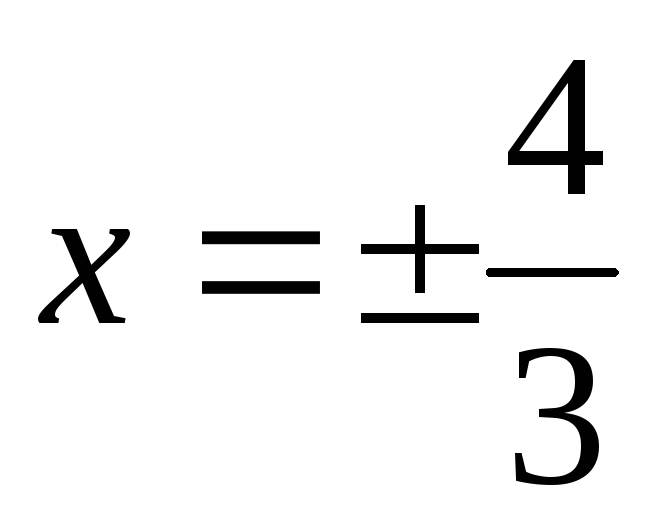 ;
; -
уравнения асимптот
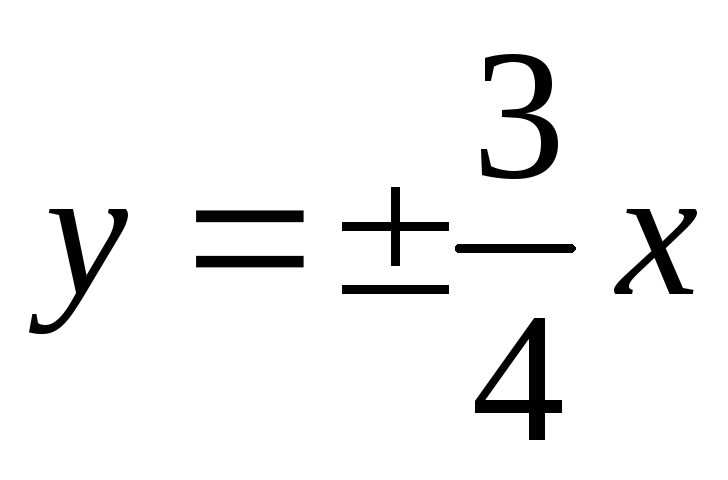 и уравнения директрис
и уравнения директрис
 .
.
№ 544
Составить уравнение гиперболы, если известны ее эксцентриситет е=5/4, фокус F(5; 0) и уравнение соответствующей директрисы 5х-16=0.
№ 546
Точка А (-3; -5) лежит на гиперболе, фокус которой F (-2;-3), а соответствующая директриса задана уравнением х+1=0. Составить уравнение этой гиперболы.
№ 550
Установив, что каждое из следующих уравнений определяет гиперболу, найти для каждой из них центр, полуоси, уравнения асимптот и построить их на чертеже:
-
xy=18; 2) 2xy-9=0; 3) 2xy+25=0.
№ 555
Определить при каких значениях m прямая y= 5/2 x +m
-
пересекает гиперболу
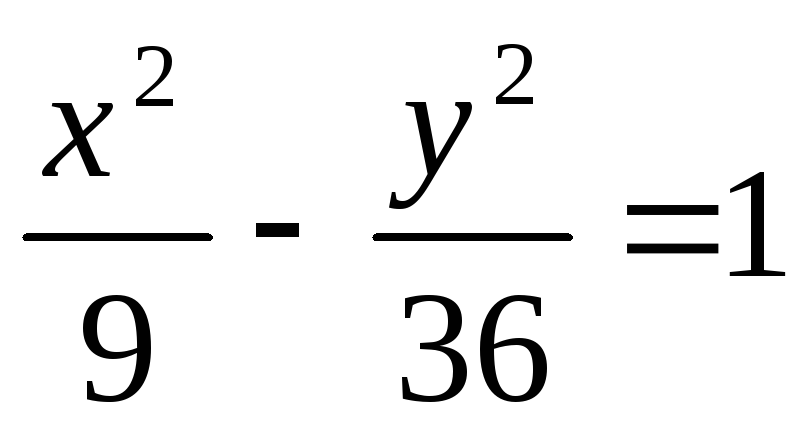 ;
; -
касается ее;
-
проходит вне гиперболы.
№ 559
Составить
уравнения касательных к гиперболе
![]() ,
перпендикулярных к прямой 4х+3y-7=0.
,
перпендикулярных к прямой 4х+3y-7=0.
№ 560
Составить
уравнения касательных к гиперболе
![]() ,
параллельных к прямой 10х-3y+9=0.
,
параллельных к прямой 10х-3y+9=0.
№ 561
Провести
касательные к гиперболе
![]() параллельно прямой 2х+4y-5=0
и вычислить расстояние d
между ними.
параллельно прямой 2х+4y-5=0
и вычислить расстояние d
между ними.
№ 562
На гиперболе найти точку М1, ближайшую к прямой 3х+2y+1=0 и вычислить расстояние d от точки М1 до этой прямой.
№ 563
Составить уравнения касательных к гиперболе х2-y2=16, проведенных из точки А(-1; -7).
№ 564
Из
точки С(1;-10)
проведены касательные к гиперболе
![]() .
Составить уравнение хорды, соединяющей
точки касания.
.
Составить уравнение хорды, соединяющей
точки касания.
№ 565
Из
точки Р(1;
-5)
проведены касательные к гиперболе
![]() .
Вычислить расстояние от точки Р
до гиперболы, соединяющей точки касания.
.
Вычислить расстояние от точки Р
до гиперболы, соединяющей точки касания.
№ 566
Гипербола
проходит через точку А(![]() ;
3)
и касается прямой 9х+2y-15=0.
Составить уравнение этой гиперболы при
условии, что ее оси совпадают с осями
координат.
;
3)
и касается прямой 9х+2y-15=0.
Составить уравнение этой гиперболы при
условии, что ее оси совпадают с осями
координат.
№ 583
Составить уравнение параболы, вершина которой находится в начале координат, зная, что
-
парабола расположена в правой полуплоскости симметрично относительно оси Ох, и ее параметр р=3;
-
парабола расположена в левой полуплоскости симметрично относительно оси Ох, и ее параметр р=0,5;
-
парабола расположена в верхней полуплоскости относительно оси Оy и ее параметр р=1/4;
-
парабола расположена в нижней полуплоскости симметрично относительно оси Оу, и ее параметр р=3.
№ 590
Вычислить фокальный радиус точки М параболы у2=20х, если абсцисса точки М равна 7.
№ 592
На параболе у2=16х найти точки, фокальный радиус которых равен 13.
№ 593
Составить уравнение параболы, если дан фокус F(-7; 0) и уравнение директрисы х-7=0.
№ 594
Составить уравнение параболы, зная, что ее вершина совпадает с точкой (а; b), параметр р.
№ 602
Составить уравнение параболы, если даны ее фокус F(-7; 0) и директриса х-у-1=0.
№ 608
В следующих случаях определить, как расположена данная прямая относительно данной параболы: пересекает, касается или проходит вне ее:
-
х-у+2=0 и у2=8х;
-
8х+3у-15=0 и х2= -3у;
-
5х-у-15=0 и у2=-5х.
№ 616
На параболе у2=64х найти точку М1, ближайшую к прямой 4х+3у-14=0 и вычислить расстояние d от точки М1 до этой прямой.
№ 617
Составить уравнения касательных к параболе у2=36х, проведенных из точки А(2; 9).
№ 618
К параболе у2=2рх проведена касательная. Доказать, что вершина этой параболы лежит посередине между точкой пересечения касательной с осью Ох и проекцией точки касания на ось Ох.
№ 619
Из точки А(5; 9) проведены касательные к параболе у2=5х. Составить уравнение хорды, соединяющей точки касания.
№ 620
Из точки Р(-3;12) проведены касательные к параболе у2=10х. Вычислить расстояние d от точки Р до хорды параболы, соединяющей точки касания.
Тема: 12 Упрощения центральной кривой второго порядка
Содержание: нахождение инвариантов кривой, определение типа кривой, в случае центрального типа - осуществление параллельного переноса и поворота систем координат, отыскание канонического уравнения кривой в каноническом репере и ее построение.
Цель: научить студентов приводить к каноническому виду общее уравнение кривой второго порядка центрального типа
Форма контроля: опрос.
Задания:
№ 665
Установить какие из следующих линий являются центральными (т.е. имеют единственный центр), какие не имеют центра, какие имеют бесконечно много центров:
-
3х2+4ху-2у2+3х-12у-7=0;
-
4х2+5ху+3у2-х+9у-12=0;
-
4х2-4ху+у2-6х+8у+13=0;
-
4х2-4ху+y2-12х+6у-11=0;
-
х2-2ху+4y2+5х-7у+12=0;
-
х2-2ху+y2-6х+6у-3=0;
-
4х2-20ху+25y2-14х+2у-15=0;
-
4х2-6xу-9y2+3х-7у+12=0.
№ 676
Каждое из следующих уравнений привести к каноническому виду; определить тип каждого из них; установить, какие геометрические образы они определяют; для каждого случая изобразить на чертеже оси первоначальной системы, оси других координатных систем, которые вводятся по ходу решения, и геометрический образ, определяемый данным уравнением:
-
3х2+10ху+3y2-2х-14у-13=0;
-
25х2-14ху+25y2+64х-64у-224=0;
-
4ху+3y2+16х+12у-36=0;
-
7х2+6xу-y2+28х+12у+28=0.
-
19х2+6ху+11y2+38х+6у+29=0;
-
5х2-2ху+5y2-4х+20у+20=0;
№ 677
Каждое из следующих уравнений привести к каноническому виду; определить тип каждого из них; установить, какие геометрические образы они определяют; для каждого случая изобразить на чертеже оси первоначальной системы, оси других координатных систем, которые вводятся по ходу решения, и геометрический образ, определяемый данным уравнением:
-
14х2+24ху+21y2-4х+18у-139=0;
-
11х2-20ху-4y2-20х-8у-8=0;
-
7х2+60ху+32y2-14х-60у+7=0;
-
50х2-8xу+35y2+100х-8у+67=0.
-
41х2+24ху+34y2+34х-112у+129=0;
-
29х2-24ху+36y2+82х-96у-91=0;
-
4х2+24ху+11y2+64х+42у+51=0;
-
41х2+24ху+9y2+24х+18у-36=0;
№ 678
Не проводя преобразования координат, установить, что каждое из следующих уравнений определяет эллипс, найти величины его полуосей:
-
41х2+24ху+9y2+24х+18у-36=0;
-
8х2+4ху+5y2+16х+4у-28=0;
-
13х2+18ху+37y2-26х-18у+3=0;
-
13х2+10xу+13y2+46х+62у+13=0.
№ 682
Не проводя преобразования координат, установить, какие геометрические образы определяются следующими уравнениями:
-
8х2-12ху+17y2+16х-12у+3=0;
-
17х2-18ху-7y2+34х-18у+7=0;
-
2х2+3ху-2y2+5х+10у=0;
-
6х2-6xу+9y2-4х+18у+14=0.
-
5х2-2ху+5y2-4х+20у+20=0;
Тема: 13 Упрощение линии параболического типа. Построение кривых.
Содержание: определение типа кривой по инвариантам, построение кривых.
Цель: сформировать навык приведения к простейшему виду общих уравнений кривых второго порядка всех типов, а также их построения.
Форма контроля: опрос.
Задания:
№ 689
Установить, что каждое из следующих уравнений являются параболическим; каждое из привести к простейшему виду; установить, какие геометрические образы они определяют; для каждого случая изобразить на чертеже оси первоначальной координатной системы, оси других координатных систем, которые вводятся по ходу решения, и геометрических образ, определяемый данным уравнением:
-
9х2-24ху+16y2-20х+110у-50=0;
-
9х2+12ху+4y2-24х-16у+3=0;
-
16х2-24ху+9y2-160х+120у+425=0.
№ 690
Установить, что каждое из следующих уравнений являются параболическим; каждое из привести к простейшему виду; установить, какие геометрические образы они определяют; для каждого случая изобразить на чертеже оси первоначальной координатной системы, оси других координатных систем, которые вводятся по ходу решения, и геометрических образ, определяемый данным уравнением:
-
9х2-24ху+16y2-18х+226у+209=0;
-
х2-2ху+y2-12х+12у-14=0;
-
4х2+12ху+9y2-4х-6у+1=0.
№ 693
Установить, что каждое из следующих уравнений является параболическим; каждое из привести к простейшему виду; установить, какие геометрические образы они определяют; для каждого случая изобразить на чертеже оси первоначальной координатной системы, оси других координатных систем, которые вводятся по ходу решения, и геометрических образ, определяемый данным уравнением:
-
х2+4ху+4y2+4х+у-15=0;
-
9х2-6ху+y2-х+2у-14=0;
-
25х2-20ху+4y2+3х-у+11=0;
-
16х2+16ху+4y2-5х+7у=0;
-
9х2-42ху+49y2+3х-2у-24=0.
№ 697
Не проводя преобразования координат, установить, что каждое из следующих уравнений определяет параболу, и найти параметр этой параболы:
-
9х2+24ху+16y2-120х+90у=0;
-
9х2-24ху+16y2-54х-178у+181=0;
-
х2-2ху+y2+6х-14у+29=0;
-
9х2-6ху+y2-50х+50у-275=0.
№ 698
 Доказать,
что уравнение второй степени является
уравнением вырожденной линии в том и
только в том случае, когда =0.
Доказать,
что уравнение второй степени является
уравнением вырожденной линии в том и
только в том случае, когда =0.
№ 700
Не проводя преобразования координат, установить, что каждое из следующих уравнений определяет одну прямую (пару слившихся прямых), и найти уравнение этой прямой:
-
х2-6ху+9y2+4х-12у+4=0;
-
9х2+30ху+25y2+42х+70у+49=0;
-
16х2-16ху+4y2-72х+36у+81=0.
Ответы:
№ 444 1)
№ 448 16 кв. ед.
№ 450
![]() кв.
ед.
кв.
ед.
№ 451 b2/c
№ 453 (-3; -8/5), (-3;8/5)
№ 454 Точки А1 и А6 лежат на эллипсе; А2, А4 и А8 –внутри эллипса; А3, А5, А7 , А9 и А10 – вне эллипса.
№ 456 15.
№ 459 r1=2,6; r2=7,4
№ 465
1)
![]() 2)
2)
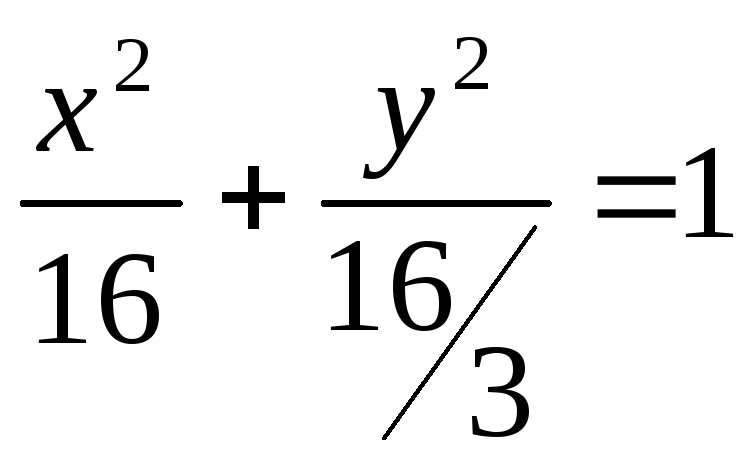 3)
3)
![]()
4)
![]() 5)
5)
![]() 6)
6)
![]()
7)
![]()
№ 483 1) прямая пересекает эллипс; 2)прямая проходит вне эллипса; 3)касается эллипса





 №
484
1) при m
<5 –
пересекает эллипс;
m
= 5
– касается эллипса; m
>5
– проходит вне эллипса.
№
484
1) при m
<5 –
пересекает эллипс;
m
= 5
– касается эллипса; m
>5
– проходит вне эллипса.
№ 488 3x +2y –10=0 и 3x +2y +10=0
№ 489 x +y –5=0 и x +y +5=0
№ 490
2x
-y
–12=0
и 2x
-y
+12=0![]()
№ 491
М1(-3;
2); d=![]()
№ 492 x +y –5=0 и x +4y -10=0
№ 493 4x -5y –10=0
№ 499
![]()
№ 515
№ 518
1) a=3;
b=4;
2) F1(
-5; 0) и F2(5;
0); 3) е=5/3; 4)
![]() 5)
5)![]()
№ 520 12 кв. ед.
№ 524 8.
№ 528 (10; 9/2); (10; -9/2)
№ 530
![]() ;
;![]()
№ 532
1)
![]()
2) х2-y2=16;
3)
![]()
4)
![]() или
или
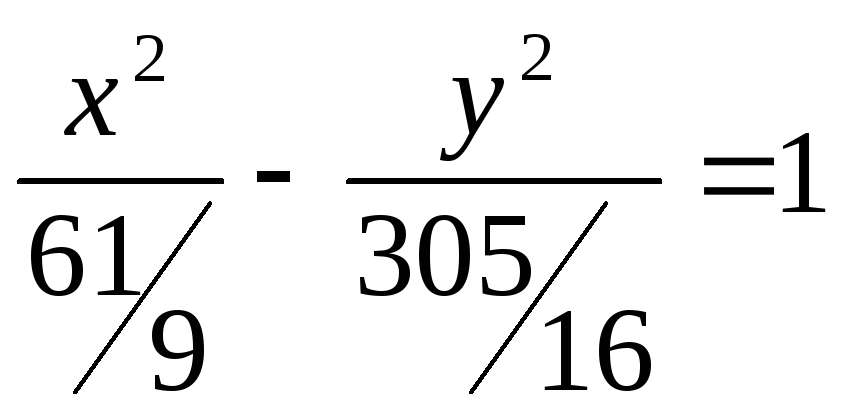
5)
![]()
№ 544![]()
№ 546 х2-4y2-6х-24у-47=0.
№ 550
-
С(0; 0), a=b=6, уравнения асимптот х=0 и у=0;
-
С(0; 0), a=b=3, уравнения асимптот х=0 и у=0;
-
С(0; 0), a=b=5, уравнения асимптот х=0 и у=0.





 №
555
1) при m
>4,5 –
пересекает гиперболу;
m
=4,5
– касается гиперболы; m
<4,5
– проходит вне гиперболы.
№
555
1) при m
>4,5 –
пересекает гиперболу;
m
=4,5
– касается гиперболы; m
<4,5
– проходит вне гиперболы.
№ 559 3x -4y –10=0 и 3x -4y +10=0
№ 560 10x -3y –32=0 и 10х-3у +32=0
№ 561
x
+2y
–4=0
и
![]()
№ 562
М1(
-6; 3) и
![]()
№ 563 5x -3y –16=0 и 13х+5у +48=0
№ 564 2x +5y +48=0
№ 565
![]()
№ 566
![]()
№ 583
1) y2=6х;
2)
y2=-х;
3)
![]() 4)
х2=-6у.
4)
х2=-6у.
№ 590 12.
№ 592 (9; 12); (9; -12)
№ 593 y2=-28х.
№ 594 1) (y-b)2=2p(х-a); ) (y-b)2=2p(х-a).
№ 602 х2+2ху+y2-6х+2у+9=0.
№ 608 1) касается параболы; 2) пересекает параболу в двух точках; 3) проходит вне параболы.
№ 616 М1(9; -24); d=10.
№ 617 3x -y +3=0 и 3х-2у +12=0
№ 619 5x -18y +25=0
№ 620
![]()
№ 665 Линии 1), 2), 5) и 8) имеют единственный центр; 3) и 7) – не имеют центра; 4) и 6) – имеют бесконечно много центров.
№ 676
-
гиперболическое уравнение; определяет гиперболу, уравнение которой приводится к виду
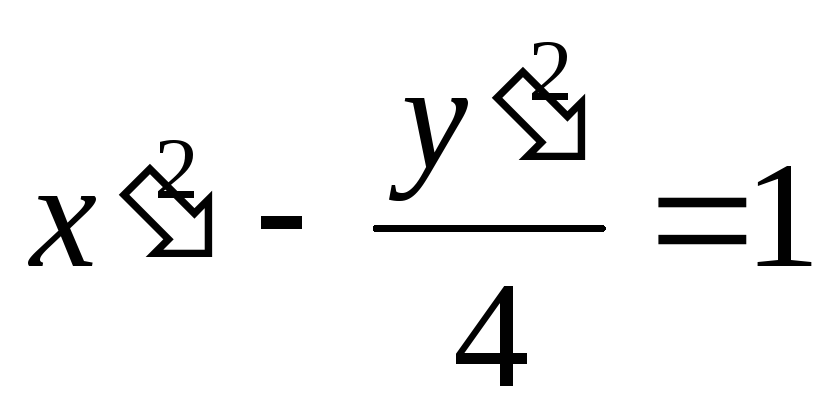 путем двух последовательных преобразований
координат:
путем двух последовательных преобразований
координат:
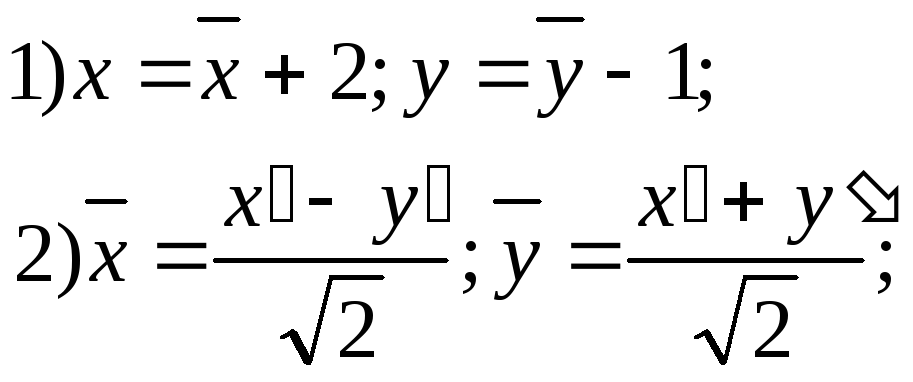
(рис. 128);
-
эллиптическое уравнение; определяет эллипс, уравнение которого приводится к виду
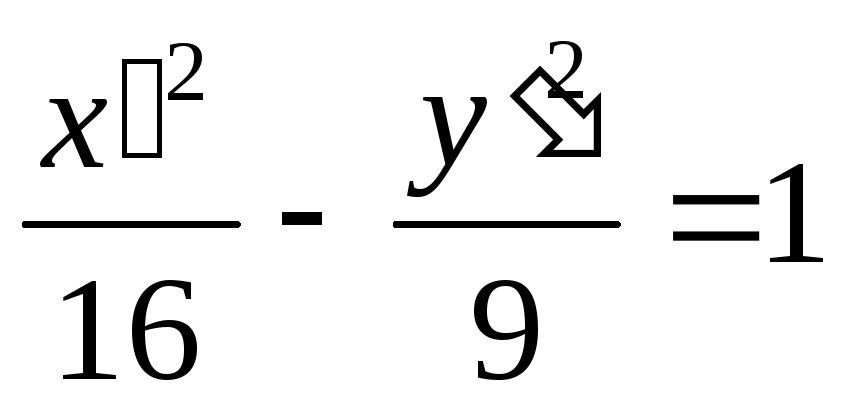 путем
двух последовательных преобразований
координат
путем
двух последовательных преобразований
координат
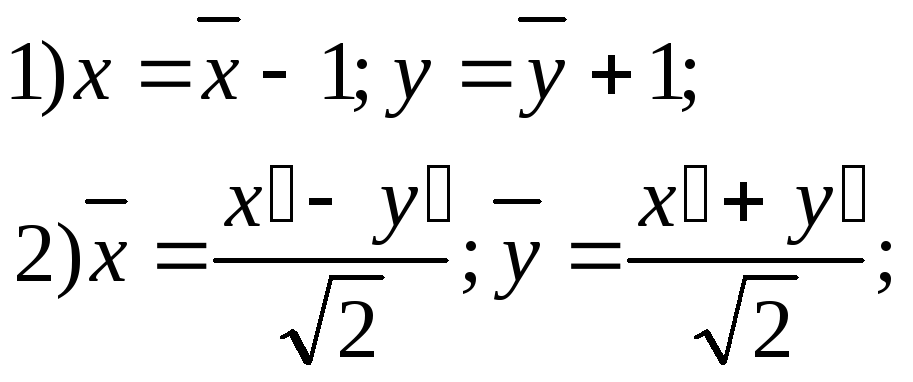
(рис. 129);
-
гиперболическое уравнение; определяет гиперболу, уравнение которой приводится к виду
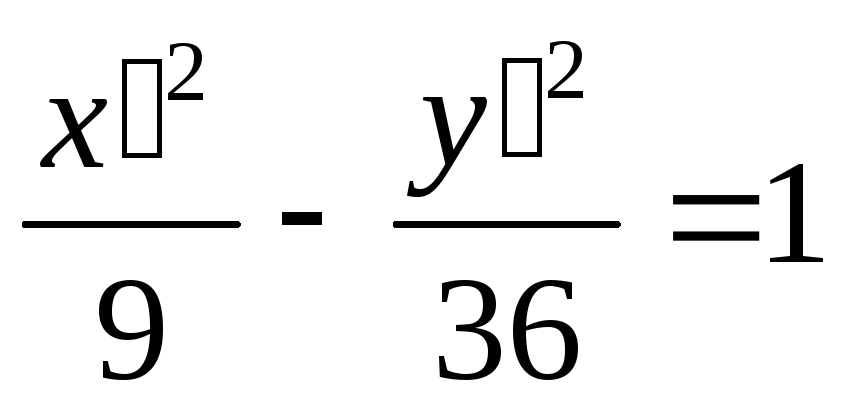 путем двух последовательных преобразований
координат:
путем двух последовательных преобразований
координат:
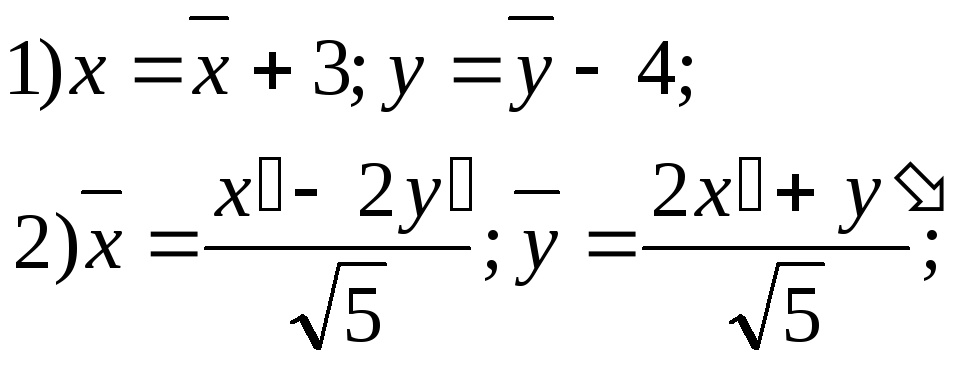
(рис. 130);
-
гиперболическое уравнение; определяет вырожденную гиперболу - пару пересекающихся прямых, уравнение которой приводится к виду х’2-4y’2=0 путем двух последовательных преобразований координат:

(рис. 131);
-
эллиптическое уравнение; не определяет никакого геометрического образа – «мнимый эллипс»; его уравнение приводится к виду х’2+2y’2=-1 путем двух последовательных преобразований координат:
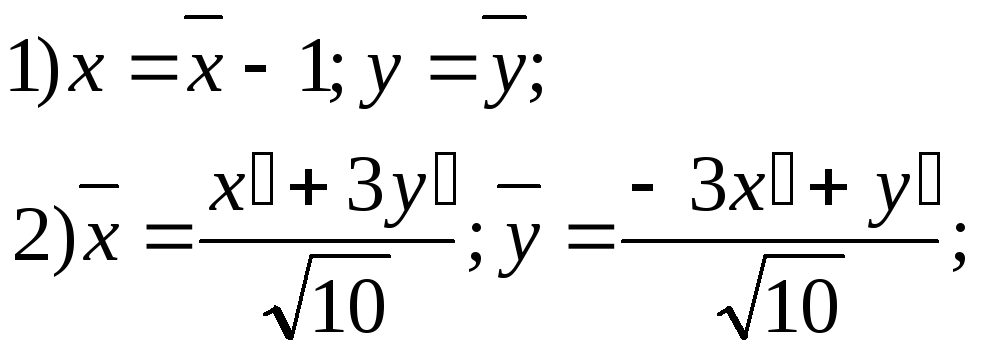 ;
;
-
эллиптическое уравнение; определяет вырожденный эллипс – единственную точку; его уравнение приводится к виду 2х’2-3y’2=0 путем двух последовательных преобразований координат:
 .
.






![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()


![]()
![]()





![]()
![]()
Рис. 128 Рис. 129






![]()
![]()
![]()
![]()
![]()


![]()
![]()




![]()
![]() ,
,
![]()

![]()
Рис. 130. Рис. 131.
№ 677
1)
![]() - эллипс;
- эллипс;
-
9х2-16y2=5 – гипербола
-
х2-4y2=0 - вырожденная гипербола – пара пересекающихся прямых, уравнения которых х-2y=0 и х+2y=0;
-
2х2+3y2=-1 – «мнимый эллипс»; уравнение не определяет никакого геометрического образа;
-
х2+2y2=0 – вырожденный эллипс4 уравнение определяет единственную точку – начало координат;
-
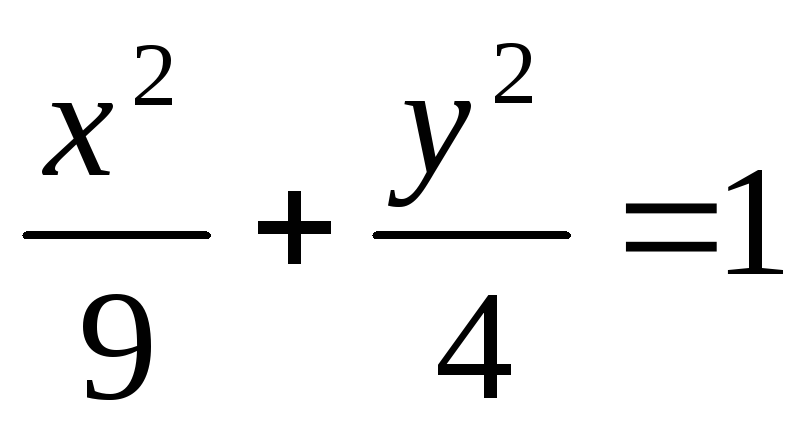 -
эллипс;
-
эллипс; -
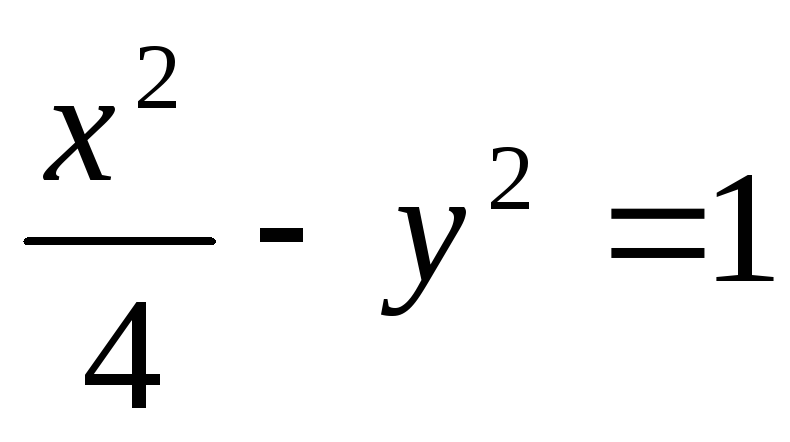 -
гипербола;
-
гипербола; -
 -
эллипс.
-
эллипс.
№ 678 1) 3 и 1; 2) 3 и 2;
3) 1 и 1/2; 4) 3 и 2.
№ 682
-
эллипс;
-
гипербола;
-
пара пересекающихся прямых (вырожденная гипербола);
-
уравнение не определяет никакого геометрического образа («мнимый эллипс»);
-
точка (вырожденный эллипс).
№ 689
-
параболическое уравнение; определяет параболу, уравнение которой приводится к виду у’’2=2x’’ путем двух последовательных преобразований координат: ХХХХХХ (рис 132);
-
параболическое уравнение; определяет вырожденную параболу - пару параллельных прямых, уравнение которых приводится к виду х’’2=1 путем двух последовательных преобразований координат: ХХХХХХ (рис 133);
-
параболическое уравнение; не определяет никакого геометрического образа; приводится к виду х’’2=1 путем двух последовательных преобразований координат: ХХХХХХ.
№ 690
-
у2=6x - парабола;
-
у2=25 - вырожденная парабола - пара параллельных прямых, уравнения которых у-5=0 и у=5=0;
-
у2=6x - вырожденная парабола - пара слившихся прямых, слившихся с осью абсцисс.





![]()
![]()
![]()
![]()


![]()
![]()



![]()
![]()
![]()
![]()

![]()

Рис. 132 Рис.133
№ 693
-
(х+2у)2+4х+у-15=0;
-
(3х-у)2-х+2у-14=0;
-
(5х-2у)2+3х-у+11=0;
-
(4х+2у)2-5х+7у=0;
-
(3х-7у)2+3х-2у-24=0.
№ 697 1) 3; 2) 3;
3)
![]() 4)
4)![]()
№ 700
-
х-3у+2=0;
-
3х+5у+7=0;
-
4х-2у-9=0.
Примеры решения задач:
Тема 10
№ 459
Убедившись,
что точка М1(-4;
2,4)
лежит на эллипсе
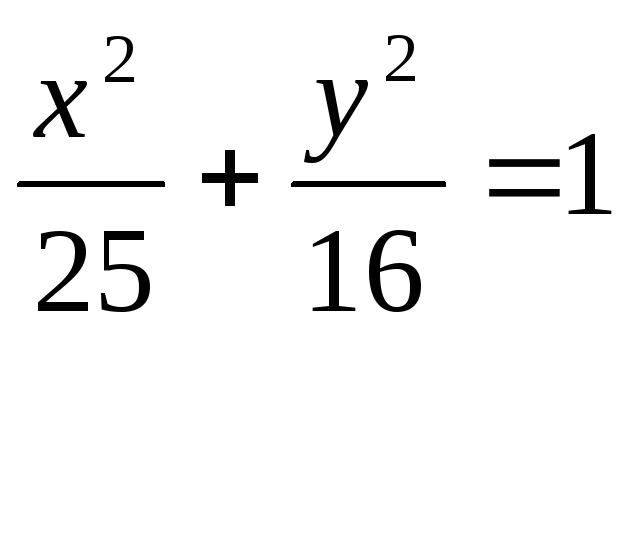 ,
определить фокальные радиусы точки М1.
,
определить фокальные радиусы точки М1.
Решение
Подставим
точку М1(-4;
2,4)
в уравнение эллипса
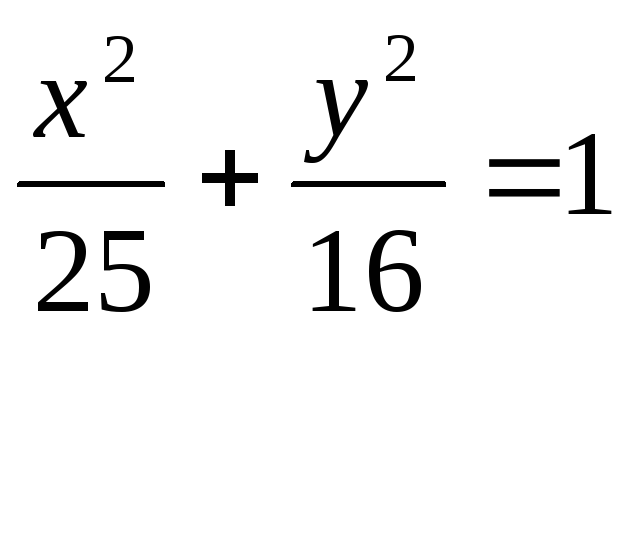
а = 5; b = 4;
c2 = a2-b2; c=3;
e = c/a = 3/5;
r1 = a + ex = 5+3/5 (-4)=2,6;
r2 = a - ex = 5-3/5 (-4) =7,4.
Ответ: r1=2,6; r2= 7,4.
№ 488
Составить
уравнения касательных к эллипсу
![]() ,
параллельных прямой 3x+2y+7=0.
,
параллельных прямой 3x+2y+7=0.
Решение
Уравнение касательных запишем в виде Аx+By+C= 0.
Поскольку они параллельны прямой 3x+2y+7=0,то А=а=3, B=b=2, а коэффициент С можно най ти с помощью уравнения Аа+Bb=C2;
C2= 90+10 = 100;
Уравнениея касательных 3x+2y+10=0 и 3x+2y-10=0.
Ответ: 3x+2y+10=0 и 3x+2y-10=0.
Тема 11
№ 518
Дана гипербола 16x2-9y2=144.Найти:
-
полуоси а и b;
-
эксцентриситет;
-
уравнения асимптот;
-
уравнения директрис.
Решение
1) а2 =144/16 = 9; а=3;
b2 = 144/9 =16; b=4;
-
c2 = a2+b2=9+16=25; c=5;
F1 (-5; 0); F2 (5; 0);
-
e = c/a = 5/3;
-
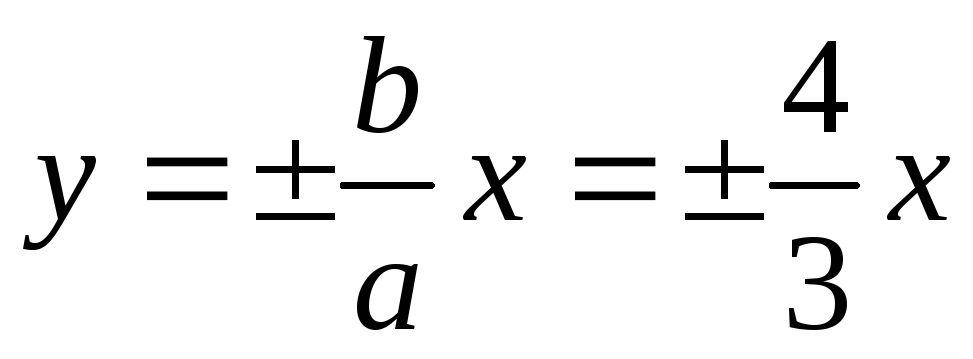
-

Ответ:
а=3;
b=4; F1
(-5;
0); F2
(5;
0); e = 5/3;
![]() ;
;
![]() ;
;
№ 528
Определить
точки гиперболы
![]() ,
расстояние которых до правого фркуса
равно 4,5.
,
расстояние которых до правого фркуса
равно 4,5.
Решение
а2 =64; а=8;
b2 =36; b=4
c2 = a2+b2=64+36=100; c=10;

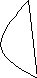 AF2
=4,5; A(x; y);
AF2
=4,5; A(x; y);
![]() А
А


![]()

 x=10;
y2=81/4:
o
x=10;
y2=81/4:
o
A(10; 9/2); A(10; -9/2). F1 F2
Ответ: A(10; 9/2); A(10; -9/2).
Тема 12
№ 678
Не проводя преобразования координат, установить, что каждое из следующих уравнений определяет эллипс, найти величины его полуосей:
-
41х2+24ху+9y2+24х+18у-36=0;
Решение

![]() составляется
из коэффициентов ри старших членах
41х2+24ху+9y2+24х+18у-36=0;
составляется
из коэффициентов ри старших членах
41х2+24ху+9y2+24х+18у-36=0;
![]()
![]()
Ответ: 1) 3 и 1.
Тема 13
№ 697
Не проводя преобразования координат, установить, что каждое из следующих уравнений определяет параболу, и найти параметр этой параболы:
-
9х2+24ху+16y2-120х+90у=0;
Решение
![]()
-
9
12
-60
 =
=12
16
45
=-140625
-60
45
0
![]()
р=3.
Ответ: 1) 3.
