10. Определение кратчайшего пути в сети методом динамического программирования
В рассматриваемой задаче граф
имеет исток
и сток
,
а каждая дуга имеет длину
.
I.Вначале рассмотримсеть без циклов.
Требуется найти путь минимальной длины
- последовательность смежных вершин
с минимальной суммой длин соединяющих
их дуг. Обозначим
расстояние между вершинами
,
положив при этом
и
,
если
.
Метод динамического программирования основан на использовании соотношений Беллмана:
.
Алгоритм решения задачи предполагает
просмотр и раскрытие всех вершин, начиная
сконечнойвершины. Раскрытие
означает присвоение вершине
пометки следующего вида:
,
где
- уже раскрытая смежнаяc
вершина,
-
длина пути из
в
кратчайшей
длины,
-
длина дуги
,
-
длина кратчайшего пути их
в
.
Алгоритм
Присвоить стоку
пометку
.
Каждой нераскрытой вершине
,
смежной с
,
присвоить пометку
,
где
Если существует нераскрытая вершина
,
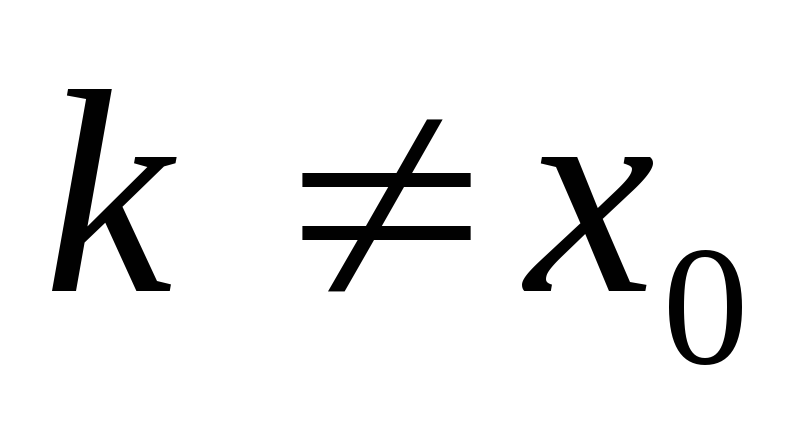присвоить ей пометку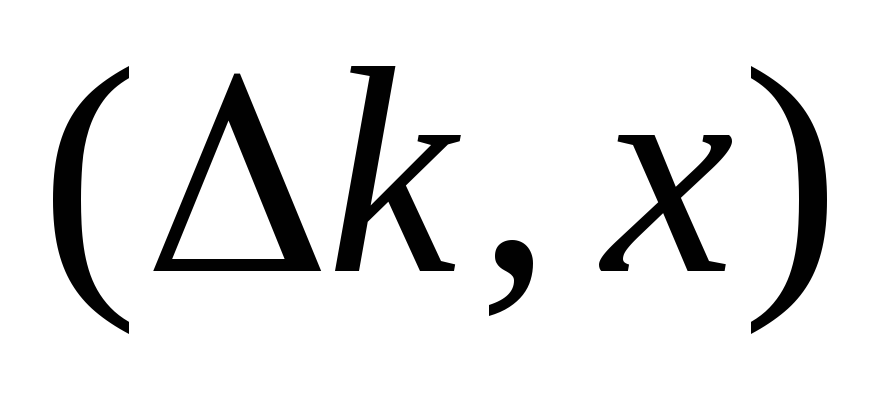
.Если исток
раскрыт, то его пометка включает длину
кратчайшего пути в сети и имя следующей
зах0 вершиной.Обратный просмотр. Двигаясь по пометкам в направлении стока, получают последовательность вершин кратчайшего пути. Конец.
Замечания: 1) кратчайший путь может быть не единственным; 2) приведенный алгоритм применим для поиска самого длинного пути в сети.
Пример. Транспортная сеть задана на рисунке ориентированным графом (рис.10.1). Над дугами проставлены их длины. Считается, что дуги в обратном направлении имеют неограниченную длину.
Рис. 10.1.
Истоку присваивается
пометка
.
Смежные с истоком вершины раскрываются
следующим образом:
,
а вершинаc
допускает три возможные пометки:
,
причем лучшей, согласно соотношению
Беллмана, является
,
т.к. кратчайший путь из
с
в z
проходит
через вершину d.
Две другие пометки в дальнейшем не
учитываются (исключаются). Аналогично
раскрывают вершины a
и b.
Наконец, исток
может быть раскрыт тремя способами,
причем две из трех пометок
и
являются лучшими. Далее выполняется
обратный просмотр, и по именам вершин
в разметке восстанавливаются два пути
минимальной длины:
или
.
Кратчайшая длина пути равна 8.
Вопросы
1. Сформулировать идею метода динамического программирования.
2. Выяснить возможность применимости метода для нахождения пути
наибольшей длины.
Задание. Определить наименьший путь в заданной сети без циклов:
Длины дуг заданы таблицей:
|
|
Варианты | |||||||||||||||||||
|
дуги |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
(1,2) |
1 |
5 |
7 |
8 |
5 |
6 |
6 |
3 |
2 |
6 |
2 |
4 |
3 |
3 |
2 |
4 |
1 |
3 |
5 |
7 |
|
(1,3) |
6 |
1 |
2 |
6 |
6 |
4 |
5 |
2 |
4 |
5 |
3 |
2 |
4 |
3 |
5 |
5 |
7 |
3 |
4 |
5 |
|
(1,4) |
4 |
6 |
2 |
3 |
4 |
4 |
5 |
6 |
2 |
3 |
4 |
5 |
5 |
6 |
6 |
5 |
8 |
4 |
6 |
6 |
|
(2,5) |
5 |
6 |
1 |
6 |
6 |
2 |
3 |
4 |
5 |
3 |
2 |
1 |
4 |
8 |
8 |
8 |
7 |
4 |
3 |
9 |
|
(3,5) |
6 |
8 |
6 |
5 |
8 |
5 |
4 |
5 |
6 |
3 |
2 |
2 |
4 |
4 |
4 |
6 |
6 |
6 |
2 |
3 |
|
(3,6) |
4 |
6 |
6 |
4 |
4 |
4 |
2 |
3 |
3 |
2 |
3 |
2 |
2 |
1 |
2 |
4 |
1 |
2 |
3 |
4 |
|
(3,7) |
5 |
5 |
5 |
4 |
3 |
4 |
3 |
2 |
2 |
2 |
2 |
4 |
4 |
5 |
2 |
6 |
6 |
3 |
5 |
6 |
|
(4,6) |
2 |
2 |
3 |
4 |
5 |
5 |
4 |
6 |
5 |
7 |
8 |
8 |
3 |
7 |
3 |
5 |
7 |
2 |
4 |
5 |
|
(5,8) |
3 |
4 |
4 |
4 |
3 |
3 |
3 |
5 |
5 |
5 |
8 |
8 |
8 |
8 |
4 |
7 |
5 |
4 |
5 |
4 |
|
(6,8) |
4 |
1 |
1 |
2 |
2 |
3 |
2 |
2 |
2 |
3 |
3 |
1 |
2 |
6 |
3 |
4 |
7 |
2 |
2 |
3 |
|
(6,9) |
4 |
2 |
2 |
4 |
5 |
6 |
4 |
3 |
5 |
6 |
7 |
8 |
4 |
4 |
5 |
7 |
4 |
5 |
6 |
5 |
|
(7,8) |
6 |
6 |
4 |
3 |
3 |
3 |
5 |
5 |
4 |
5 |
6 |
4 |
5 |
5 |
6 |
3 |
3 |
2 |
1 |
2 |
|
(8,9) |
4 |
4 |
5 |
6 |
3 |
6 |
6 |
5 |
3 |
4 |
2 |
3 |
3 |
3 |
2 |
5 |
2 |
7 |
7 |
1 |
II. Пусть в
транспортной сети имеютсяциклы.
В этом случае формулируется такая
задача: найти кратчайшие пути из вершины
в каждую из оставшихся вершин.
В сети с циклами расстояние между двумя
смежными вершинами может оказаться не
самым коротким. Рассмотрим пару смежных
вершин i иjcдлиной
соединяющей их дуги. Пусть
- числовые пометки, равные длинам
кратчайших путей из
.
Для каждой вершины
.
Очевидно, если
,
то цепь из
в вершинуjне образует
кратчайший путь, и следует произвести
корректировку:
.
Если же для любой смежных пары вершинi иjвыполнено условие
,
то задача решена.
Алгоритм
Найти какие-либо цепи из начальной вершины в остальные и вычислить
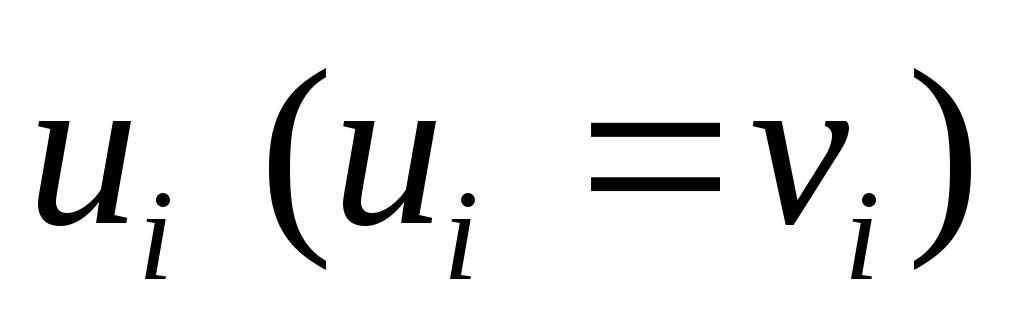.Если при просмотре некоторой пары смежных вершин оказалось, что
,
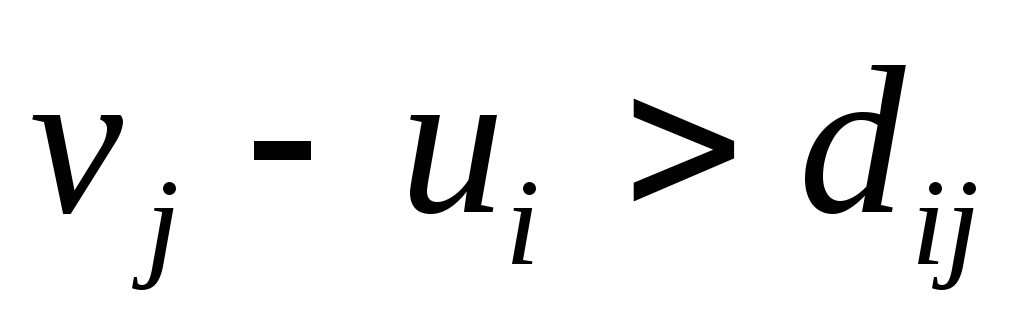произвести пересчет:
.Если при очередном просмотре всех пар смежных вершин коррекции нет, завершить задачу.
Пример.Дан граф на рис. 10.2 с вершинами 1,2,3,4 и проставленными длинами дуг.
Рис. 10.2.
Первоначальные
значения пометок соответствуют длинам
некоторых путей из вершины 1 в остальные:
.
Перебор пар смежных дуг удобно записать
в таблицу (табл.10.1.). В каждой строке
выполняется проверка неравенств
.
Таблица 10.1.
-
j
i
1
2
3
4
-
-
1-0
1
4-0
4
3-0
3
-1
3
-
-
4-1
2
-
-
-
-
1-3
2
-
-
-
-
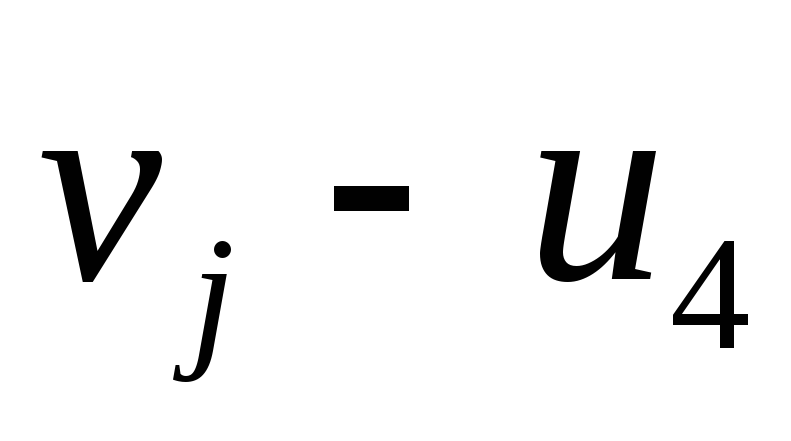
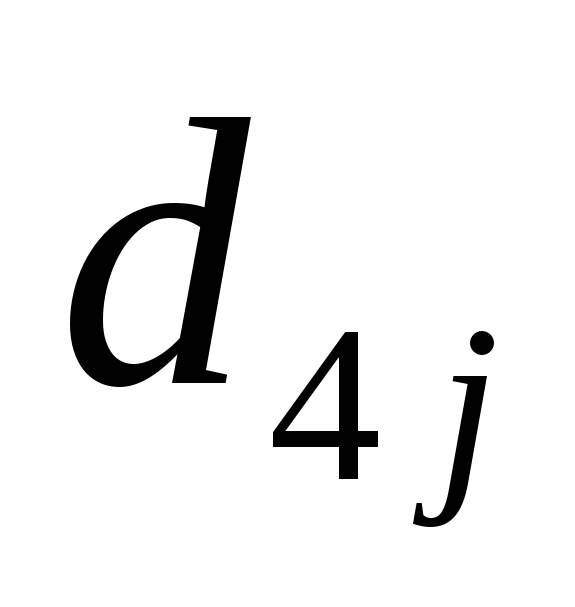
0-3
2
1-4
2
3-3
1
-
-
Для пары смежных
вершин 2 и 3 условие
не выполнено: 3>2. Производится
корректировка:
.
В дальнейшем используется это уже
откорректированное значение. При
повторном просмотревсех
пар смежных вершин неравенство
истинно. Кратчайшие пути из вершины 1
в остальные таковы:
.
Задание. На рисунке приведена сеть, содержащая циклы. Для каждой вершины определить кратчайший путь из вершины 1. Длины дуг задать произвольными целыми числами от 1 до 10.
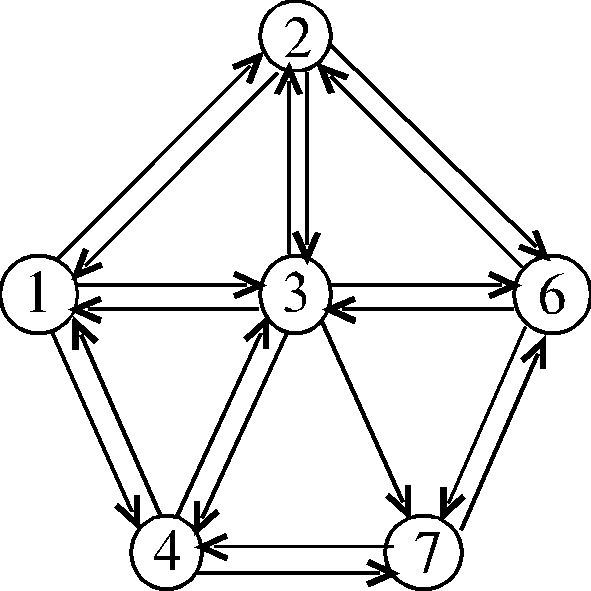
Рис. 10.3.