9. Нахождение максимального потока в сети

Многие задачи исследования операций сводятся к анализу потоков, маршрутов, последовательностей событий, протекающих во времени, и других процессов, которые можно представить в виде множества взаимосвязанных элементов. Для математического представления таких процессов удобно их задание в виде графов.

Пусть - конечное множество. Зафиксируем подмножество.Рассмотрим конечный ориентированный граф,в котором - множество вершин, - множество дуг.

Определение. Транспортной сетью (Т-сетью) называется конечный ориентированных графГ, в котором выделены две особые вершины:– исток иz– сток, и на множестве дугопределена функция.

Примерами функций дуги могут быть длина дуги, пропускная способность, поток и другие.

Таким образом, .

Пусть . Обозначим- множество дуг графаГ, входящих в вершину х,- выходящих изх. Соответствующие множества вершин обозначими.

y

y

x

Рис.9.1.

Очевидно, что .

Вершина называетсяистоком,z -стоком.

Пропускной способностьюдуги называется функция.

Каждая дуга имеет некоторую фиксированную пропускную способность.

Потокомдуги называют функцию, удовлетворяющую условиям:

Здесь - естьвходящий потокдля некоторой вершиныx,

-выходящий потокиз вершиныx.

Условие 2) означает, что поток не накапливается в вершине. Дуги, в которых поток равен пропускной способности , называютсянасыщенными.

Поток, входящий в вершину , не ограничен. ПотокФ, выходящий из истокав Т-сеть, называетсяпотоком в сети. Из условия 2) следует:

.

Поток Фназываетсяполным, если каждая цепь извzсодержит хотя бы одну насыщенную дугу. Два полных потока одной сети могут иметь различную величину. Полный поток в сети является стационарным.

Задача о нахождении максимального потока в сетисостоит в следующем: для заданной Т-сети требуется определить потоки во всех дугах так, чтобы полный потокФбыл максимальным.

Разрезом Т-сети называется разбиениеRмножества вершин сети на два подмножества:. Сумма пропускных способностей дуг множестваопределяет пропускную способность, иливеличину разрезаR:

В транспортной сети можно построить различные разрезы. Среди них существует разрез минимальной величины:

.

Задача нахождения минимального разреза является двойственной к задаче о максимальном потоке в сети.

Теорема (Форда-Фалкерсона).Максимальный поток в сети равен величине минимального разреза в этой сети:.

Алгоритм нахождения максимального потока, предложенный Фордом и Фалкерсоном, состоит в постепенном увеличении допустимого потока Фдо максимального. Начальное значение потоков дуг полагается равным нулю. Процесс увеличения потока состоит в поиске цепей в графе, ведущих из истока в сток, на которых возможно увеличение потока, с соответствующей разметкой (раскрытием) вершин сети.

Общий вид пометки j-й вершины, смежной с уже раскрытой i-й вершиной, следующий: . Знак «+» записывается, если вершинапредшествует вершине(т.е. ); знак «-» – если вершина следует за вершиной(). Величина показывает, на сколько единиц может быть увеличен входящий поток или уменьшен выходящий:

.

Алгоритм Форда-Фалкерсона

I.Увеличение потока

1. Присвоить истоку пометку. Это означает, что вход в исток не ограничен.

2. Взять некоторую раскрытую вершину с пометкой. Произвольной нераскрытой вершине, для которой, присвоить пометку. В случае, еслииприсвоить ей пометку.

3. Если можно раскрыть какую-либо вершину, то перейти к п. 2.

4. Если достигнут сток с пометкой, то во всех дугах цепи из ввеличина потока изменяется:, еслиили, если. Затем стереть все пометки и перейти к п.1.

5. Если ни одну вершину раскрыть не удается, и сток не достигнут, то перейти к построению разреза.

II. Построение разреза

, где- все вершины, допускающие раскрытие, - вершины, которые не удается пометить. При этомполный поток должен быть равен величине полученного минимального разреза. Конец.

Пример. Пусть задана транспортная сеть с пропускными способностями, записанными над дугами (рис.9.2). Начальные потоки равны нулю.

Рис. 9.2

На первом шаге раскрыты вершины цепи . Сток достигнут с пометкой, и поток в цепи увеличен на 2 единицы. Дугастала насыщенной. Пометки стерты (рис.9.3). Выполняется поиск других возможных цепей.

На втором шаге поток увеличен на 1 единицу вдоль цепи . Насыщенной стала дуга.

Рис. 9.3.

На следующем шаге очевидно, что сток недостижим. При этом вершинаможет быть раскрыта двумя способами:по дугеилипо дуге.

Рис.7.4.

Строится разрез . Его величина. Максимальный поток.

Вопросы

1. Дать определение транспортной сети, потока, разреза.

2. Сформулировать теорему о максимальном потоке.

Задание. Найти максимальный поток в заданной транспортной сети:

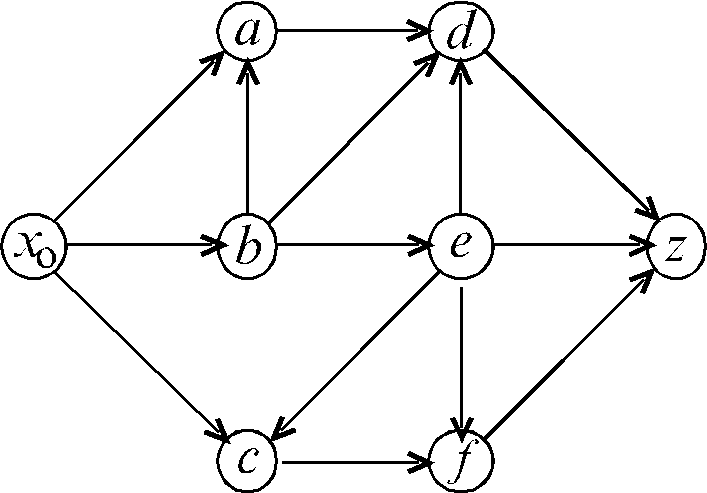
Пропускные способности дуг задать произвольно целыми числами от 1 до 10. При оформлении работы повторить рисунок сети не менее трех раз.