Algebra_10kl_RU
.pdf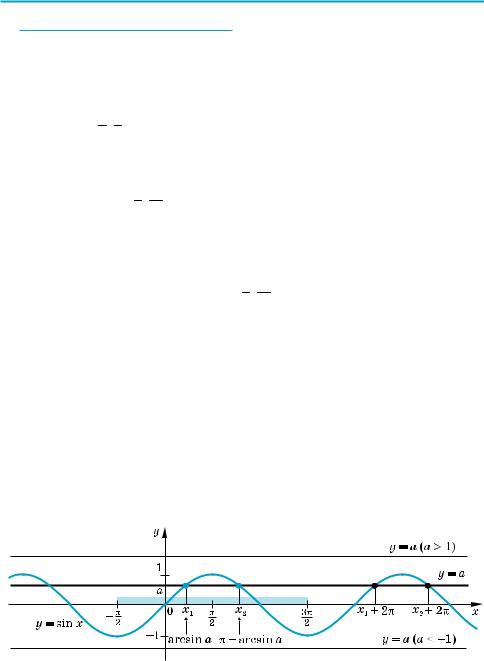

РАЗДЕЛ 2. Тригонометрические уравнения и неравенства |
|||||||
Задача 2 |
Решите уравнениe sinx = π . |
||||||
|
|
|
|
|
|
2 |
|
|
Р е ш е н и е |
К о м м е н т а р и й |
|||||
X Поскольку |
|
π |
>1, то корней нет. |
Поскольку π >1, то данное урав |
|||
|
2 |
2 |
|||||
Ответ: корней нет. Y |
|
нение не имеет корней (то есть фор |
|||||
|
мулой (3) нельзя воспользоваться). |
||||||
|
|
|
|
|
|
||
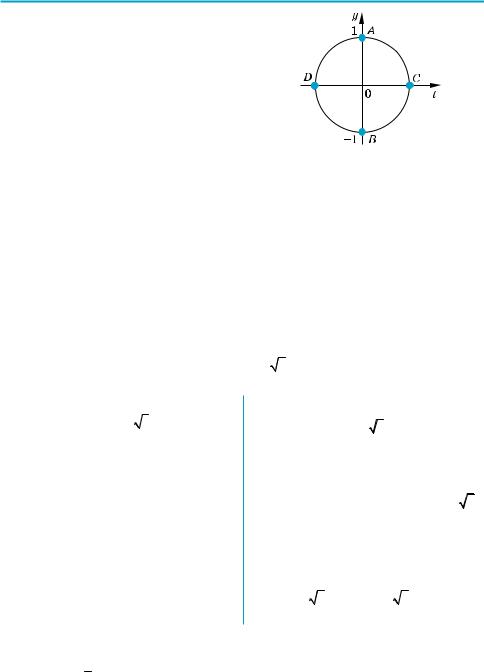
Задача 3 |
Решите уравнение sin(2x + 4π)= 21 . |
||||||
|
Р е ш е н и е |
К о м м е н т а р и й |
|||||
X 2x + π = (−1)n arcsin 1 + πn, n Z, |
Поскольку 1 <1, то можно вос |
||||||
4 |
|
|
|
2 |
|
2 |
|
2x + π = |
(−1)n π + πn, |
пользоваться формулой (3) для на |
|||||
|
4 |
|
|
6 |
хождения значения выражения |
||
|
n |
π |
π |
|
πn |
2x + π , а потом из полученного ли |
|
x = (−1) |
12 |
− 8 |
+ |
2 , n Z. |
|||
|
π |
|
π |
πn |
|
4 |
|
n |
|
|
нейного уравнения найти перемен |
||||
Ответ: (−1) 12 |
− |
8 + |
2 |
, n Z. Y |
ную х. |
||
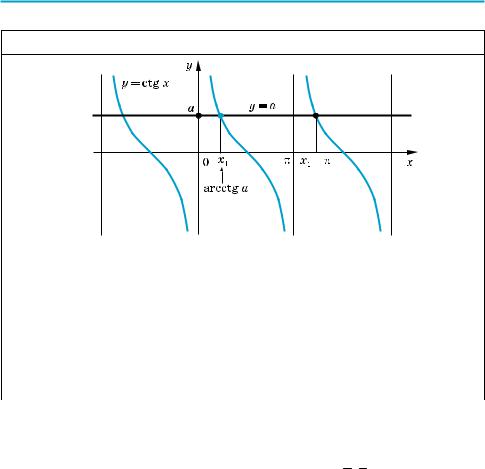
14.3. УРАВНЕНИЯ tg x = a и ctg x = a |
|
||||||
|
|
|
|
|
|
Т а б л и ц а 32 |
|
1. Графическая иллюстрация и решения уравнения tg x = a |
|||||||
|
Формула |
|
Пример |
||||
|
tg x = a |
|
tg x = 1. |
||||
x = arctg a + πn, n Z |
|||||||
X x = arctg 1 + πn, n Z. |
|||||||
Частный случай |
|||||||
x = π + πn, n Z. Y |
|||||||
|
tg x = 0 |
|
|||||
|
|
4 |
|||||
х = πn, n Z |
|
||||||
|
|
|
|
|
|
164 |
|