Файловый архив студентов. Файловый архив студентов.
1295 вузов, 5022 предметов.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Таврический Национальный Университет им. В.И. Вернадского
Предмет:
[НЕСОРТИРОВАННОЕ]
Файл:

Algebra_10kl_RU

.pdf
Скачиваний:
126
Добавлен:
20.03.2015
Размер:
5.2 Mб
Скачать
☆

РАЗДЕЛ 2. Тригонометрические уравнения и неравенства

 

а функция f (x) — обратной к функции

 

g (x). Поэтому говорят, что функции

 

f (x) и g (x) взаимно обратные.

 

Из определения обратной функции

 

вытекает, что область значений пря

 

мой функции E (f) является областью

 

определения обратной функции D (g),

 

а область определения прямой функ

 

ции D (f) является областью значений

 

обратной функции E (g).

Рис. 84

То есть:

 

E (f) = D (g), D (f) = E (g).

2. Свойства обратной функции.

 

С в о й с т в о 1. Графики прямой и обратной функций симметричны

относительно прямой у = х.

(Учитывая приведенную выше процедуру построения функции, обратной к функции у =f (x), имеем: если f (a) = b, то по определению графика функции точка M с координатами (a; b) принадлежит графику функции y = f (x).

Аналогично, поскольку g (b) = a, то точка M1 с координатами (b; a) принад лежит графику функции y = g (x). Точки M (a; b) и M1 (b; a) расположены на координатной плоскости симметрично относительно прямой y = x (рис. 84). Действительно, прямая y = x является осью симметрии системы коорди нат. Таким образом, при симметрии относительно этой прямой ось Оx ото бражается на ось Оy, а ось Оy — на ось Оx. Тогда (например, при a > 0 и b > 0) прямоугольник OAMD со сторонами OA = a и OD = b на осях коорди

нат отображается на прямоугольник OA1M1D1 со сторонами на осях коор динат OA1 = OA = a и OD1 = OD = b. Следовательно, при симметрии относи тельно прямой y = x точка M (a; b) отображается в точку M1 (b; a) (а точ ка M1 — в точку M). Таким образом, при симметрии относительно прямой y = x любая точка M (a; b), принадлежащая графику функции y = f (x),

имеет соответствующую точку M1 (b; a), принадлежащую графику функ ции y = g (x), а любая точка M1 (b; a), которая принадлежит графику функ ции y = g (x), имеет соответствующую точку M (a; b), принадлежащую гра фику функции y = f (x). То есть графики взаимно обратных функций сим метричны относительно прямой y = x. )

С в о й с т в о 2. Если функция f (x) возрастает (убывает) на некото

ром промежутке, то она имеет обратную функцию на этом проме жутке, которая возрастает, если f (x) возрастает, и убывает, если f (x) убывает.

(Действительно, если функция f (x) возрастает (убывает) на некотором про межутке, то по свойству возрастающей (убывающей) функции каждое свое значение она принимает в единственной точке из этого промежутка (с. 14), таким образом, она имеет обратную функцию g (x) на этом промежутке.

142

§ 12. Обратная функция

Обосновать, что функция g (x) возрастает, если f (x) возрастает, можно методом от противного.

Пусть числа а1 и а2 входят в область определения функции f (x) и

 

а2 > а1.

(1)

Обозначим f (а1) = b1, f (а2) = b2. Если функция f (x) возрастает, то f (а2) > f (а1), то есть b2 > b1. По определению обратной функции g (x) числа b1 и b2 входят

в ее область определения и

g (b1) = а1, g (b2) = а2.

(2)

Если допустить, что функция g (x) не является возрастающей, то из нера венства b2 > b1 не может вытекать неравенство g (b2) > g (b1) (иначе функция g (x) будет возрастающей), таким образом, может выполняться только не равенство g (b2) m g (b1). Но тогда по формулам (2) получаем a2 m a1, что противоречит условию (1). Таким образом, наше предположение неверно, и функция g (x) возрастает, если функция f (x) возрастает.

Аналогично обосновывается, что в случае, когда функция f (x) убывает, обратная к ней функция g (x) тоже убывает. )

3. Практический прием нахождения формулы функции, обратной к функ ции y = f (x). Из определения обратной функции следует, что для получения обратной зависимости необходимо знать, как значение x выражается через зна чение y. Это можно сделать, решив уравнение y = f (x) относительно пе ременной x. Если заданная функция обратима, то уравнение будет иметь един ственное решение для всех y из области значений функции f (x), и мы получим формулу x = g (y), которая задает обратную функцию. Но в этой формуле аргу мент обозначен через y, а функция — через x. Если поменять обозначения на традиционные, то получим запись функции, обратной к функции y = f (x).

Эти рассуждения вместе с соответствующим алгоритмом приведены в таб лице 25 и реализованы в решении следующих задач.

Примеры решения задач

 

Найдите функцию, обратную к функции y =

1

.

Задача 1

 

 

 

x − 1

 

Р е ш е н и е

X Областьопределения: х ≠ 1. Тогда

из равенства y =

1

имеем

 

 

x − 1

ху – у = 1, ху = у + 1, x = y + 1.

y

Обозначим аргумент через x, а функцию — через y и получим функ

цию y = x x+ 1 , обратную к заданной. Y

К о м м е н т а р и й

На всей области определения (х ≠ 1) заданная функция обратима, посколь

ку из уравнения y =

1

можно одно

 

 

x − 1

значно выразить x через y (у ≠ 0 в об ласти значений заданной функции).

Полученная формула x = y + 1 задает

y

обратную функцию, но в ней аргумент обозначен через y, а функция — через x. Изменяя обозначения на традици онные, получаем конечный результат.

143

РАЗДЕЛ 2. Тригонометрические уравнения и неравенства

Задача 2

 

Найдите функцию, обратную к функции y = х2.

 

 

 

Р е ш е н и е

 

К о м м е н т а р и й

 

 

 

 

X Из равенства y = х2 при y l 0 по

 

Область значений заданной функ

лучаем x = ±

y. Тогда при y > 0 одно

 

ции: y l 0. Но при y > 0 из равенства

му значению y соответствуют два зна

 

y = x2 нельзя однозначно выразить x

 

через y. Например, при y = 4 получа

чения x. Таким образом, на всей об

 

 

ем x = ä 2. Вследствие этого мы не мо

ласти определения x (–×; +×) фун

 

 

жем значению y = 4 поставить в соот

кция y = x2 не является обратимой,

 

и для нее нельзя найти обратную

 

ветствие единственное число, чтобы

 

построить обратную функцию.

функцию. Y

 

 

 

 

 

 

 

 

Найдите функцию, обратную к функции y = х2 при x l 0.

Задача 3

 

 

 

 

Р е ш е н и е

 

К о м м е н т а р и й

 

 

 

 

X Из равенства y = х2 при y l 0 по

 

Множество значений заданной

лучаем x = ±

y. Учитывая, что по ус

 

функции: y l 0. При x l 0 заданная

ловию x l 0, имеем x = y.

 

функция y = х2 возрастает, таким об

 

разом, на промежутке x l0 она имеет

Обозначим аргумент через x, а

 

 

обратную функцию, а значит, на этом

функцию — через y и получим, что

 

 

промежутке уравнение х2 = y мы смо

функцией, обратной к функции

 

жем решить однозначно: при x l 0

y = х2, которая задана только при

 

 

имеем x = y.

x l 0, будет функция y = x. Y

 

 

Эта формула задает обратную

 

 

 

 

 

 

 

 

 

 

функцию, но в ней аргумент обозна

 

 

 

 

 

чен через y, а функция — через x. Из

 

 

 

 

 

меняя обозначения на традиционные,

 

 

 

 

 

получаем конечный результат.

 

 

 

 

 

 

Рис. 85

З а м е ч а н и е. В примерах 2 и 3 мы фактически рассматриваем различ ные функции (они имеют разные об ласти определения), хотя в обоих слу чаях эти функции задаются одной и той же формулой. Как известно, гра фиком функции y = х2 (пример 2) является парабола, а графиком фун кции y = х2 при x l 0 (пример 3) явля ется только правая ветвь этой пара болы (рис. 85).

144

§ 12. Обратная функция

Вопросы для контроля

1.При каком условии для заданной функции y = f (x) можно построить об ратную функцию?

2.Объясните построение графика обратной функции на примере функции y = f (x), которая задана таблицей:

x

0

2

4

6

 

 

 

 

 

f (x)

1

3

5

7

 

 

 

 

 

Задайте обратную функцию y = g (x) с помощью таблицы:

x

g(x)

3.Как расположены графики прямой и обратной функций, если они постро ены в одной системе координат? Проиллюстрируйте соответствующее свой ство графиков на примере.

4*. Обоснуйте взаимное расположение графиков прямой и обратной функций.

5.Существует ли обратная функция к функции y = x2, где x m 0? Объясните ответ, опираясь на соответствующие свойства обратной функции. Если обратная функция существует, то задайте ее формулой вида y = g (x).

Упражнения

1.Запишите формулу, которая задает функцию y = g (x), обратную к задан ной. Укажите область определения и множество значений функции g (x):

1°) y = 3x – 6; 2°) y = – 3x – 6; 3)

y =

2

;

4)

y = −

1

;

5) y = x.

x

x

 

 

 

 

 

 

 

2.На одном рисунке постройте графики данной функции и функции, обрат ной к данной:

1°) y = 2x; 2°) y = x – 2; 3) y = −

1

;

4*) y =

1

; 5*) y = x + 1.

x

 

 

 

 

x − 1

3.Найдите функцию, обратную к данной на заданном промежутке, и по стройте на одном рисунке графики данной функции и функции, обратной к данной:

1) y =

1

x2 при x l 0;

2) y =

1

x2 при x m 0;

4

4

 

3) y = (x – 2)2 при x l 2;

4) y = x2 – 2 при x m 0.

145

§13 ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ

Для получения обратных тригонометрических функций для каждой три гонометрической функции выделяется промежуток, на котором она возрас тает (или убывает). Для обозначения обратных тригонометрических функ ций перед соответствующей функцией ставится буквосочетание «arc» (чита ется: «арк»).

13.1. ФУНКЦИЯ y = arcsin x

Т а б л и ц а 26

 

1. График

y = sin x

y = arcsin x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

На промежутке

−

π

;

π sin x возра

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

стает.

 

 

 

 

 

2

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2. Значение arcsin a (| a | m 1)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Ориентир

 

 

 

 

 

 

 

 

 

 

 

 

 

Пример

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

arcsin а — это такое число из проме

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

жутка −

π

;

π

, синус которого ра

 

 

 

 

 

 

 

 

3

=

π

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

arcsin

 

 

 

 

 

 

 

 

 

 

 

, так как

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

3

 

вен а.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

π

 

− π

 

 

π

 

 

 

 

 

 

 

 

 

 

π

 

3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

π

 

π

 

 

 

 

 

 

 

 

 

 

 

 

 

 

=

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ϕ −

 

;

 

,

 

 

3

2 ;

 

 

2

и sin

3

 

2 .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

arcsin a = ϕ, если

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

sinϕ = a

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3. Нечетность функции y = arcsin x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

arcsin (–a) = –arcsin a

146

§ 13. Обратные тригонометрические функции

Объяснение и обоснование

1. График функции y = arcsin x. Функция y = sin x возрастает на промежутке

− π ; π и принимает все значения от –1 до 1. Следовательно, на этом проме

2 2

жутке функция y = sin x имеет обратную функцию, которая обозначается

y = arcsin x, с областью определения [– 1; 1] и областью значений − π ; π .

2 2

Функция y = arcsin x также возрастает, и ее график можно получить из гра фика функции y = sin x (на заданном промежутке) с помощью симметричного отображения относительно прямой y = x (рис. 86).

2. Значение arcsin a. По определению обратной функции (на выбранном про

 

 

π

 

π

 

межутке), если sin ϕ = a, то arcsin a = ϕ, причем ϕ

−

 

;

 

 

и | a | m 1. Таким

2

 

 

 

 

2

 

образом, запись arcsin a = ϕ (| a | m1) означает, что ϕ − π ; π и sin ϕ = a, то есть

2 2

arcsin a — это такое число из промежутка − π ; π , синус которого

равен a.

2 2

 

1

 

π

 

 

 

 

π

 

π

 

π

 

 

 

 

π

 

 

 

1

 

 

 

Например, arcsin

 

=

 

 

, поскольку

 

−

 

;

 

 

и sin

 

 

 

=

 

.

 

 

 

 

 

6

2

 

 

 

 

 

 

 

2

 

6

 

 

 

 

 

 

2

 

 

 

6

 

 

 

2

 

 

)= −

 

 

 

 

 

3

 

π

 

 

 

 

 

 

π

 

 

π

 

 

π

и sin(−

π

Аналогично arcsin −

 

 

= −

 

, поскольку

−

 

 

−

 

;

 

 

 

 

 

 

 

 

 

2

 

3

 

 

 

 

 

 

3

 

 

2

 

 

2

 

 

3

 

3 .

2

3. Нечетность функции y = arcsin x. Для нахождения арксинусов отрица тельных чисел можно также пользоваться нечетностью функции arcsin x, то есть формулой: arcsin (–a) = –arcsin a.

(Это следует из того, что график функции y = arcsin x (рис. 86) симметричен относительно начала координат, а также из того, что точки a и (–a) на оси Оy (рис. 87) симметричны относительно оси Оx. Тогда и соответствую

Рис. 86

Рис. 87

147

РАЗДЕЛ 2. Тригонометрические уравнения и неравенства

щие точки A и B на единичной окружности (на промежутке − 2π ; 2π ) так же будут симметричными относительно оси Оx. Таким образом, COA = = COB. Но arcsin a = COA, а arcsin (–a) = – COB (рисунок 87 приведен для случая а > 0). Получаем

arcsin (–a) = –arcsin a . )

Например, arcsin(−

1

)= −arcsin

1

= −

π

.

 

 

 

 

 

 

 

 

 

2

2

6

 

 

 

 

 

 

1) sin(arcsin

1

);

2*) cos(arcsin

3

).

Пример.

Найдите:

 

 

 

 

 

 

 

3

 

 

5

 

 

 

 

 

 

Ре ш е н и е

1)X Пусть arcsin 1 = ϕ, тогда по оп

3

ределению арксинуса получаем,

что

sinϕ = 1 .

3

Таким образом,

sin(arcsin 13 )= sinϕ = 13. Y

2) X Пусть arcsin 3 = ϕ. По определе

5

нию арксинуса получаем, что

 

π

 

π

3

 

 

 

 

 

 

ϕ −

 

;

 

и sinϕ =

 

. Учитывая,

2

 

5

 

 

2

 

 

 

 

 

 

что cos ϕ l 0, имеем:

 

 

 

 

 

 

cosϕ =

 

1− sin2 ϕ =

 

1− (

3

)2

=

4

.

 

 

 

 

 

 

 

 

 

 

5

 

5

 

Таким образом,

cos(arcsin53 )= cosϕ = 54.Y

Ко м м е н т а р и й

1)Так как запись ϕ = arcsin a (| a | m1)

означает, что ϕ − π ; π и sin ϕ = a,

2 2

то всегда выполняется равенство

sin (arcsin a) = a, | a | m 1 .

Эту формулу можно не запоми нать: достаточно обозначить вы# ражение в скобках через ϕ и при# менить определение арксинуса.

2)Если обозначить выражение в скобках через ϕ, то по требова

нию задачи необходимо найти cos ϕ. Использовав определение арксинуса, получаем стандартную задачу: зная синус угла, найти его косинус, если угол находится на

промежутке − π ; π .

2 2

Тогда cosϕ = ± 1 − sin2 ϕ . Так как

ϕ − π ; π , то на этом промежут

2 2

ке cos ϕ l 0, таким образом,

cosϕ = 1− sin2 ϕ.

148

§13. Обратные тригонометрические функции

13.2.ФУНКЦИЯ y = arccos x

 

 

 

 

 

 

Т а б л и ц а 27

1. График

 

 

 

 

 

 

 

 

y = cos x

 

y = arccos x

 

 

 

На промежутке [0; π] cos x убывает.

 

 

 

 

 

 

 

 

2. Значение arccos a (| a | m 1)

 

 

 

 

 

 

Ориентир

 

 

Пример

 

 

 

 

arccos a — это такое число из про

 

 

 

 

 

 

 

 

межутка [0; π], косинус которого

arccos

2 = π , так как

равен а.

 

 

 

2

4

 

 

 

 

ϕ [0; π],

π

[0;

π]

и cos

π

=

2

.

arccos a = ϕ, если

4

 

 

cosϕ = a

 

 

 

4

 

2

 

3. Формула для arccos (–a)

 

 

 

 

 

 

 

arccos (–a) = π – arccos a

Объяснение и обоснование

 

 

 

 

 

 

 

 

1. График функции y = arccos x. Функция y = cos x убывает на промежутке [0; π] и принимает все значения от 1 до –1. Таким образом, на этом промежут ке функция y = cos x имеет обратную функцию, которая обозначается

149

РАЗДЕЛ 2. Тригонометрические уравнения и неравенства

Рис. 88

Рис. 89

y = arccos x, с областью определения [–1; 1] и областью значений [0; π]. Функция y = arccos x также убывает, и ее график можно получить из графика функции y = cos x (на заданном промежутке) с помощью симметричного ото бражения его относительно прямой y = x (рис. 88).

2. Значение arccos a. По определению обратной функции (на выбранном про межутке), если cos ϕ = a, то arccos a = ϕ, причем ϕ [0; π] и | a | m 1. Таким образом, запись arccos a = ϕ (| a | m 1) означает, что ϕ [0; π] и cos ϕ = a, то есть

arccos a — это такое число из промежутка [0; π], косинус которого

равен a.

Например, arccos

1

=

π

, поскольку

π

[

π

]

и

cos

π

=

1

.

 

 

 

 

2

3

3

0;

 

3

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3

 

5π

 

 

 

 

5π

[0; π] и cos

5π

 

3

 

Аналогично arccos

−

 

=

, поскольку

= −

.

 

 

 

 

 

2

 

6

 

 

 

 

6

 

 

 

 

6

 

2

 

3. Формула для arccos (–a). Для нахождения арккосинусов отрицательных чисел можно также пользоваться формулой arccos (–a) = π – arccos a.

(Это следует из того, что точки a и (–a) на оси Оx (рис. 89) являются сим

метричными относительно оси Оy. Тогда и соответствующие точки A и B на единичной окружности (на промежутке [0; π]) также будут симметрич ными относительно оси Оy. Таким образом, COA = DOB, значит,COB = π – DOB = π – COA. Но arccos a = COA, а arccos (–a) = COB = = π – COA. Получаем

 

 

 

arccos (–a) = π – arccos a

.

Например, arccos (−

 

)

 

 

 

 

 

 

1

= π − arccos

1

= π − π =

2π

.

 

 

 

3

2

2

3

 

 

Отметим, что равенство arccos (–a) = π – arccos a означает, что функция y = arccos x не является ни четной, ни нечетной.

150

 

 

§ 13. Обратные тригонометрические функции

 

Пример.

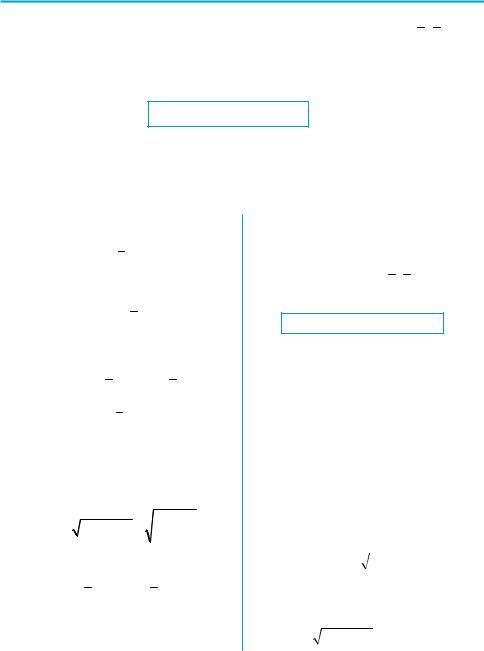
Найдите cos(arccos 2 ).

 

 

 

 

 

 

 

 

3

 

 

 

 

 

 

Р е ш е н и е

 

К о м м е н т а р и й

X Пусть arccos 2 = ϕ, тогда по опреде

Поскольку запись ϕ = arccos a

 

 

3

 

 

(| a | m 1) означает, что ϕ [0; π] и

лению арккосинуса получаем, что

cos ϕ = a, то всегда выполняется ра

 

 

 

 

 

cosϕ = 2 . Таким образом,

 

венство

 

 

 

3

 

 

 

 

cos (arccos a) = a, | a | m 1 .

cos (arccos 2 )= cosϕ = 2 .

 

Y

Эту формулу можно не запоми

 

 

3

3

 

нать: достаточно обозначить выраже#

 

 

 

 

 

ние в скобках через ϕ и применить

 

 

 

 

 

определение арккосинуса.

13.3. ФУНКЦИЯ y = arctg x

 

 

 

 

 

 

 

 

 

 

 

 

 

Т а б л и ц а 28

 

 

 

 

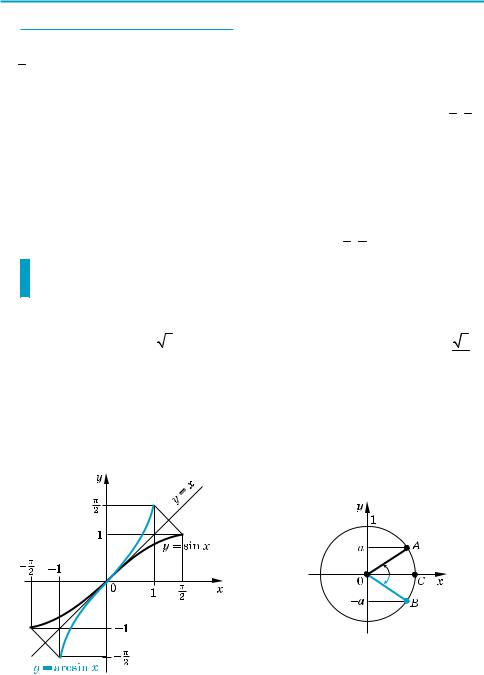
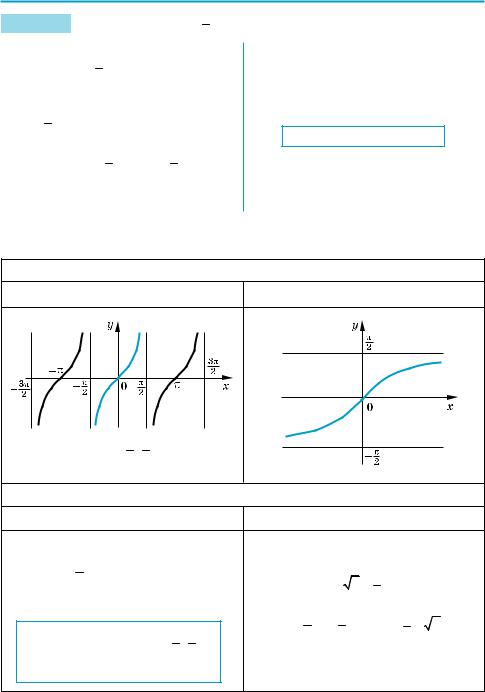
1. График

 

 

 

 

 

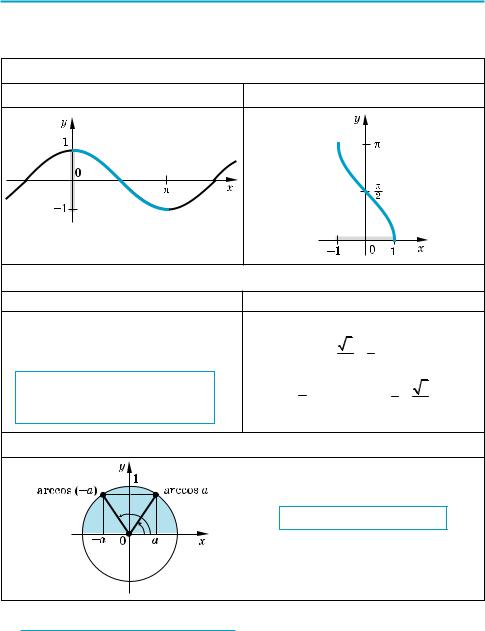
y = tg x

 

 

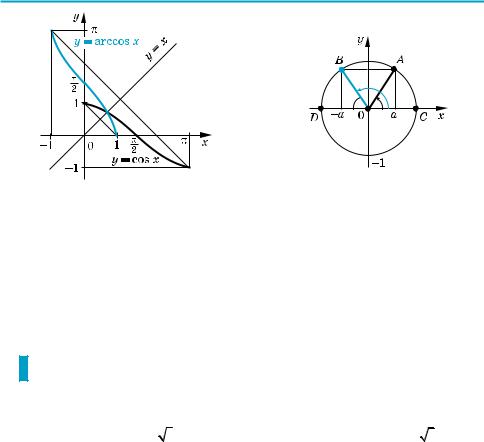
y = arctg x

На промежутке (− π ; π ) tg x возрас

 

 

 

 

тает.

 

2

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2. Значение arctg a

 

 

 

 

 

Ориентир

 

 

Пример

arctg a — это такое число из проме

 

 

 

 

жутка (− π ;

π ), тангенс которого

 

 

3 =

π , так как

равен а.

2

2

 

 

arctg

 

 

 

 

π (− π ; π )

3

 

 

 

 

π ),

и tg π = 3.

 

 

 

3

2

2

3

 

 

ϕ (− π ;

 

 

 

 

arctg a = ϕ, если

2

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

tgϕ = α

 

 

 

 

 

 

 

 

 

 

151

 

 

 
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности