
Logica_uristiv-Konversky
.pdfV . |
141 |
/ # «/» :
/=Df { / U i Q ( )}
–: «/» #« », # «U» Q(a)». ! , – «U» – $ % -
% " , «Q(a)» – «», «/» – $ .
% , !!
, .
3 , # ' , . 5 , -
,
! ,. / # # -' # , '' -
« ».
+ #. 8 " # .
+ # 2n --! . (2 -: , !
; ), n – ,. ! , $ «/»
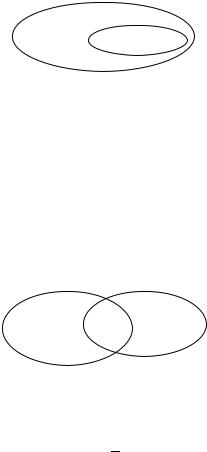
% {1, 2, 3}. 9 " 2n -$ 0 $: 23 = 8. 9- ' $ $ «/»:
{{1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3}, }.
C # # " . C #-«/» # «$» , # # «/» # «$». + " « ». 4-& «/» «$» : «/ $». + «/» , «$» – -
.
$" :
) |
, |
) |
. |
142 |
. . . |
«/» «$» " - , «/» «$» , «/ = $». 6 :
«/ $».
«/» «$», «/ $», ( «$» - , # «/»). 4 : «/ $».
0 # , # -" # . *« », «Q», -# , # '« » & «Q( )» -# .
! , % " «Q( )» – Q – -« », « » - $ : «9 », «+ », «Q », ) , $ -(«9 – », «+ – », «Q –
» ) ).
/ # , «Q( )» -« Q». / , « » # - # :
Q Q( )
–« Q ,Q». 5 -, # «Q( )»,# :
( Q) /( )
– « ,, ,
».
0 ' &- ', , ' & ':
9 |
7 |
1 |
|
|
|
a, b, …, n |
x Q(x) |
Q(a), Q(b), …, Q(n) |
|
|
|
V . |
143 |
5 ' & ' - : Q(a), Q( ), ... Q(n), – -«Q( )», . / ,' & ' # & : W Q( ) – W – 6 –# .
$ # & :
–Q( ) – ’ ;
–Q( ) – ;
–W Q( ) – .
6. < >
% , – # , " # # ' #. , -« » – /( ) « » – $( ).
C # " :
1. W /( ) W$( ) = ( W /( ) W $( )) –
«% /( )$( ), - « » ,« » /( ),
$( ).
4 ' ,« » /( ),/( ).
% # :
2. W /( ) = /( ).
3 1 :
3. W /( ) W $( ) = (/( ) $( )).
0 3 #. ' –
(W /( ) W $( ))
" # W /( ) W $( ),
(/( ) $( ))
– " # .
144 |
. . . |
: «%
,,
, ».
B " , , , - " , # . B - , , # , " " -.
, « $» –" ,# , "« $ », "« $ », " . / # .
7.
+ '. $ # # # :
;
;
;
, . + ,
( ) . 8 |
|
|
|
. |
|
B |
|
- |
. ! , « », «
», « » .
+ # :
) # ;
) .
8 . % ,
, -
, ,. ! , «$ +-
», « » .
% , -,
V . |
145 |
. ! , «$ <-
, $ < », « » . C #:
(/( ) & /( )).
.
" |
, - |
|
. ! , «- |
», « 7 0» .
3 ( ), " . % – – -( ' ' ').
+ , . ! ,
« », « », « » .
+ , -
|
. |
|
+ |
|
, |
|
, , |
|
. ! , « -
», « ’ », « », « », « »
. = « ’»( ), # : « ’ -
», « ’ 6 » .
8 . ! , « »,
« », « » .
4 # (« -< 0 3.M », «N 0 » ) («" -
», « » ).
/ , ,, # - .
+ ,
. |
|
|
L |
|
, |
|
|
! |

146 . . .
. ! , « », « », «»
.
/ ,. !-
, « », « ' », « » .
+ ,
|
|
, |
- |
. |
|
|
|
B |
|
, |
|
, |
- |
||
|
! . |
||
! , « », « ' », «-», « » .
8 |
, |
|
|
|
, |
|
! . !- |
|
, |
« », « », «- |
|
» .
7 ,,
, -- . ! , « -
» – « », « » – « », «- » – « », « » – « » ).
< ,. ! ,
« " », « », « » . / , -
-. 3 «». 5,. 3« ».
5 ’ ( " # "-# ), . $ -# -. / ,.
V . |
147 |
/ ,# .
' -
. !- , « ». A # . % # , – 1) -
, 2) , 3) , 4) .
8. < >
4’ " -" # .
5 ,
. $ -
|
. |
B |
, |
, - . ! , « » « », « »
« », « » « » .
8 ,. ! ,
« », « », « », « », « », « '- » .
+ .
7 ,
! . ! , « – », « – - » .
/( ) $( ) =Df ( Wx A(x) & x Wx B(x)) – « /( )
$( ) , %
0% %».
6 -
: |
|
) |
( - |
|
); |

148 |
|
|
. . . |
) |
|
; |
|
) |
|
. |
|
> |
, - |
||
. / # –, , -. ! , « » « ,
», « 0 » « , - ' 3 M » .
/ # -( , , -). / , – ,# ( ). ! , « »
–« », « » – « » .
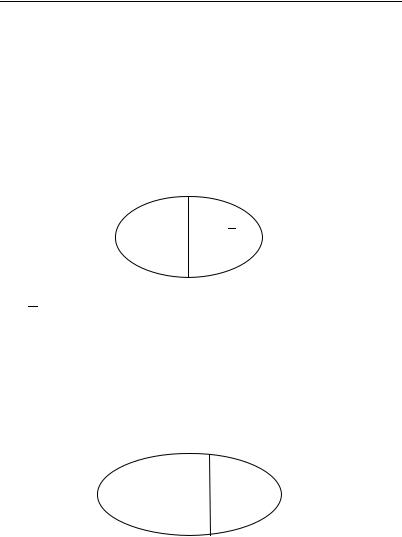
/( ) # $( ) = ( Wx A(x) x Wx B(x)) & x (x Wx B(x) x Wx A(x)) – , «-/( ) # $( ) ,- « » , « » Wx A(x),« » Wx B(x) - « » , -« » Wx B(x), « » Wx A(x)».
7 1:
Wx A(x),
Wx B(x)
$ #. !, «
» – « », « » – «$», « » – « » ).
B , -« », ,
«- ». / , « » ,« » – :
/( )
$( ) =Df ( Wx A(x)
x Wx B(x)) & x (x Wx B(x) x Wx A(x)) –
1 $" # # «* =- » ( GVIII . –
= ).
V . |
149 |
, « /( ) $( ), - « » , « » Wx A(x), « » Wx B(x), - « », « » x
B(x), « » Wx A(x)». |
|
|
7 |
|
: |
|
Wx A(x) |
|
|
Wx B(x) |
|
> |
|
|
, |
|
. !- |
, « » – « », « » – « '- » ).
/( ) $( ) =Df ( Wx A(x) &
&x Wx B(x)) & ( Wx A(x) & x Wx B(x)) –
, « /( ) $( ) , « » - , Wx /(x) Wx B(x), - « » Wx A(x) Wx B(x)».
7 :
Wx A(x) Wx B(x)
8 ,
! -.! , « » – « -
», « » – « » ).
/( ) $( )Df = ( Wx A(x) & Wx B(x))
–« /( ) $( ), « », - # Wx A(x) Wx B(x)».
150 . . .
8:
) ; ) ;
) |
. |
> |
, |
,
- . ! , «$ < » – « », « -
» – « », « » – « - » .
7 :
Wx A(x) Wx A(x)
/ « » xA x! « -
» xA x! – ,' « -
» xC x!.
B ,. 6 -' , ,. ! , « »
– « », « » – « » ).
@ # |
# : |
|
Wx A(x) |
|
Wx B(x) |
|
||
|
|
|
Wx (x)
0 « » /( ) « » $( ),' ( ,,« » 7( ).
