
1) ,,; 2),,.
Задача 29.
Даны вершины треугольника
![]() .
Найти уравнения медианы
.
Найти уравнения медианы![]() ,
биссектрисы
,
биссектрисы![]() ,
высоты
,
высоты![]() ,
если:
,
если:
1)
![]() ,
,![]() ,
,![]() ; 2)
; 2)![]() ,
,![]() ,
,![]() .
.
Задача 30*.
Даны уравнения
двух сторон прямоугольника
![]() ,
,![]() и уравнение его диагонали
и уравнение его диагонали![]() .
Составить уравнения остальных сторон
и второй диагонали этого прямоугольника.
.
Составить уравнения остальных сторон
и второй диагонали этого прямоугольника.
Задача 31.
Даны прямая
![]() и точка
и точка![]() .
Найти проекцию
.
Найти проекцию![]() точки
точки![]() на прямую
на прямую![]() и точку
и точку![]() ,
симметричную точке
,
симметричную точке![]() относительно данной прямой, если:
относительно данной прямой, если:
1)
![]() ,
,![]() ; 2)
; 2)![]()
![]() .
.
Задача 32. Определить угол между прямыми:
1)
 2)
2)![]() 3)
3)![]()
Задача 33.
Найти расстояние точек
![]() ,
,![]() ,
от прямой
,
от прямой![]() ,
если
,
если
1)
![]() ,
,![]() ,
,![]() ;
;
2)
![]() ,
,![]() ,
,![]() .
.
Задача 34. Показать, что прямые параллельны и найти расстояние между ними, если
1)
![]() ; 2)
; 2)![]()
Задача 35.
Даны вершины треугольника
![]() .
Найти длину высоты треугольника, которая
опущена из вершины
.
Найти длину высоты треугольника, которая
опущена из вершины![]() ,
если:
,
если:
1)
![]() ,
,![]() ,
,![]() ; 2)
; 2)![]() ,
,![]() ,
,![]() .
.
Задача 36. Составить уравнения биссектрис углов, образованных пересекающимися прямыми:
1)
![]() 2)
2)![]()
Задача 37.
Написать уравнение прямой, проходящей
через точку
![]() пересечения прямых
пересечения прямых![]() ,
,![]() и
и
а) проходящей через
точку
![]() ;
;
б) параллельной
оси
![]() ;
;
в) параллельной
оси
![]() ;
;
г) параллельной
прямой
![]() ;
;
д) перпендикулярной
к прямой
![]() .
.
Решить задачу, не
находя точки
![]() .
Если
.
Если
1)
![]() ,
2)
,
2)![]() .
.
Задача 38*.
Даны две вершины
![]() и
и![]() треугольника
треугольника![]() и точка
и точка![]() пересечения его медиан. Составить
уравнения сторон треугольника.
пересечения его медиан. Составить
уравнения сторон треугольника.
Задача 39*.
Дан треугольник с вершинами
![]() ,
,![]() ,
,![]() .
Найти расстояние вершины
.
Найти расстояние вершины![]() от биссектрисы угла
от биссектрисы угла![]() .
.
Задача 40*.
Даны две вершины
![]() и
и![]() треугольника
треугольника![]() и точка
и точка![]() пересечения его высот. Найти третью
вершину
пересечения его высот. Найти третью
вершину![]() .
.
§ 3. Линии второго порядка. Канонические уравнения
Окружность
Окружность есть геометрическое место точек плоскости, равноудалённых от одной и той же точки, называемой её центром.
Каноническое
уравнение окружности
с центром
![]() и радиусом, равным
и радиусом, равным![]() :
:
![]() . (14)
. (14)
Если в уравнении (17) раскрыть скобки, то мы получим общее уравнение окружности:
![]() . (15)
. (15)
Задача 41. Найти центр и радиус окружности
![]() .
.
Решение. Для решения задачи приведём данное уравнение к виду (14).
Сгруппируем отдельно слагаемые, содержащие
 и
и :
:
![]() .
.
Дополним выражения в скобках до полного квадрата суммы или разности:
![]() .
.
Свернём полные квадраты:
![]() .
.
Сравнивая это
уравнение с уравнением (15), получаем,
что
![]() ,
,![]() ,
,![]() .
.
Таким образом,
данная окружность имеет центр в точке
![]() и радиус
и радиус![]() .
.
Задачи для самостоятельного решения
Задача 42. Составить уравнение окружности в каждом из следующих случаев:
окружность проходит через начало координат и её центр совпадает с точкой
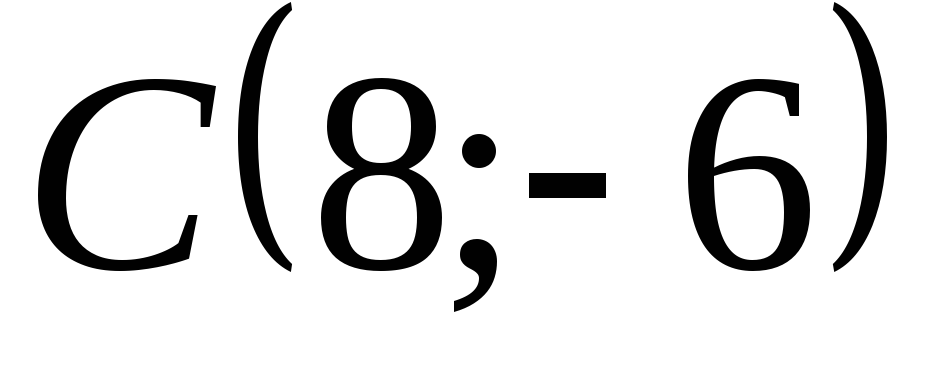 ;
;точки
 и
и являются концами одного из диаметров
окружности;
являются концами одного из диаметров
окружности;диаметром окружности является отрезок прямой
 ,
заключённй между осями координат;
,
заключённй между осями координат;окружность проходит через три точки
 ,
, ,
, ;
;окружность проходит через точки
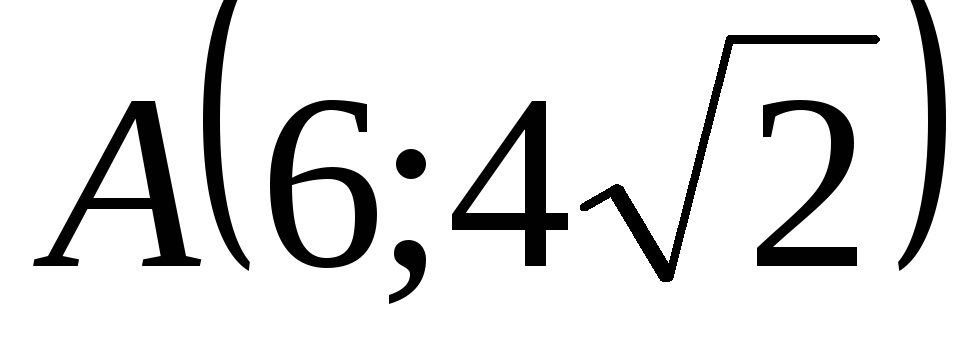 ,
, ,
центр находится на оси
,
центр находится на оси ;
;окружность касается осей координат и проходит через точку
 .
.
Задача 43. Определить центр и радиус окружности, заданной уравнением:
1)
![]() ;
;
2)
![]() ;
;
3)
![]() ;
;
4)
![]() ;
;
5)
![]() .
.
Задача 44.
Найти точки пересечения окружности
![]() с прямыми:
с прямыми:
1)
![]() ;
;
2)
![]() ;
;
3)
![]() .
.
Задача 45.
Найти угол между радиусами окружности
![]() ,
проведёнными в точки пересечения её с
осью
,
проведёнными в точки пересечения её с
осью![]() .
.
Задача 46. составить уравнение общей хорды двух окружностей:
1)
![]() и
и![]() ;
;
2)
![]() и
и![]() .
.
Эллипс
Эллипсом
называется геометрическое место точек
плоскости, сумма расстояний, которых
от двух фиксированных точек, называемых
фокусами эллипса, есть величина постоянная
(![]() ),
большая чем расстояние между фокусами
(
),
большая чем расстояние между фокусами
(![]() )
(Рис. 10).
)
(Рис. 10).
П ростейшее
(каноническое) уравнение эллипса мы
получим, если выберем прямую, соединяющую
фокусы, за ось абсцисс и поместим начало
координат в середине между ними. Тогда
уравнение эллипса примет вид:
ростейшее
(каноническое) уравнение эллипса мы
получим, если выберем прямую, соединяющую
фокусы, за ось абсцисс и поместим начало
координат в середине между ними. Тогда
уравнение эллипса примет вид:
![]() ,
(16)
,
(16)
где
![]() .
(17)
.
(17)
Точки
![]() ,
,![]() ,
,![]() ,
,![]() пересечения эллипса с осями называютсявершинами
эллипса. Отрезки
пересечения эллипса с осями называютсявершинами
эллипса. Отрезки
![]() и
и![]() называются соответственнобольшой
и малой осью эллипса,
параметры
называются соответственнобольшой
и малой осью эллипса,
параметры
![]() и
и![]() ,
входящие уравнение (16), называютсябольшой и
малой полуосями.
,
входящие уравнение (16), называютсябольшой и
малой полуосями.
Эксцентриситетом эллипса называется отношение расстояния между фокусами к его большой оси, т. е.
![]() .
(18)
.
(18)
Очевидно, что
![]() .
.
Расстояние точки
![]() эллипса от его фокусов (фокальные
радиус-векторы)
определяются формулами
эллипса от его фокусов (фокальные
радиус-векторы)
определяются формулами
![]() ,
, ![]() .
(19)
.
(19)
Директрисами
эллипса называются две прямые,
перпендикулярные большой оси эллипса
и отстоящие от его центра на расстоянии,
равном
![]() .
Уравнения директрис:
.
Уравнения директрис:
![]() ,
, ![]() . (20)
. (20)
Задача 47.
Составить каноническое уравнение
эллипса, зная, что его малая полуось
равна 16, а эксцентриситет
![]() .
.
Решение. Каноническое уравнение эллипса имеет вид (16):
![]() .
.
По условию задачи
малая ось
![]() ,
отсюда,
,
отсюда,![]() .
Известно, что
.
Известно, что
![]() .
.
Так как из (17)
![]() ,
то
,
то
![]() .
.
Следовательно, каноническое уравнение эллипса имеет вид
![]() .
.
Задача 48.
На эллипсе
![]() найти точку, расстояние которой от
правого фокуса в четыре раза больше её
расстояния от левого фокуса.
найти точку, расстояние которой от
правого фокуса в четыре раза больше её
расстояния от левого фокуса.
Решение.
Пусть точки
![]() искомая
точка. Расстояние точки
искомая
точка. Расстояние точки![]() от фокусов эллипса определяется формулами
(19):
от фокусов эллипса определяется формулами
(19):
![]() ,
, ![]() ,
,
где
![]() расстояние
от правого фокуса,
расстояние
от правого фокуса,![]() расстояние
от левого фокуса.
расстояние
от левого фокуса.
По условию задачи
![]() .
.
Подставим выражение
для эксцентриситета
![]() ,
получим
,
получим
![]() .
.
Далее, приведём уравнение данного эллипса к каноническому виду:
![]() .
.
Тогда
![]() ,
,![]() .
Следовательно,
.
Следовательно,![]() .
Таким образом,
.
Таким образом,
![]() .
.
Так как точка
![]() принадлежит эллипсу, то, подставив
принадлежит эллипсу, то, подставив![]() в его уравнение, получим
в его уравнение, получим![]() :
:
![]() .
.
Итак,
![]() .
.
Задачи для самостоятельного решения
Задача 49. Найти координаты вершин, оси, фокусы, эксцентриситет и уравнения директрис эллипсов:
|
1)
|
3)
|
|
2)
|
4)
|
Задача 50. Составить каноническое уравнение эллипса, зная, что:
его полуоси равны
 и 2;
и 2;его большая ось равна 10, а расстояние между фокусами равно 8;
его малая ось равна 24, а расстояние между фокусами равно 10;
расстояние между фокусами равно 6, эксцентриситет
 ;
;его большая ось равна 20, эксцентриситет
 ;
;его малая ось равна 6 и точка
 принадлежит эллипсу;
принадлежит эллипсу;расстояние между его директрисами равно 5, а расстояние между фокусами равно 4;
его большая ось равна 8, а расстояние между его директрисами равно 16;
его малая ось равна 6, а расстояние между его директрисами равно 13;
расстояние между его директрисами равно 32, а эксцентриситет равен
 ;
;он проходит через точку
 и эксцентриситет равен
и эксцентриситет равен ;
;он проходит через точку
 и её расстояние от левого фокуса равно
20.
и её расстояние от левого фокуса равно
20.
Задача 51.
Найти точки эллипса
![]() ,
расстояние которых до правого фокуса
равно 14.
,
расстояние которых до правого фокуса
равно 14.
Задача 52.
Найти точки эллипса
![]() ,
расстояние которых до левого фокуса
равно 2,5.
,
расстояние которых до левого фокуса
равно 2,5.
Задача 53. Найти длину хорды эллипса, которая делит пополам угол между осями, если:
1)
![]() ;
;
2)
![]() .
.
Задача 54.
Составить уравнение прямой, проходящей
через левый фокус и нижнюю вершину
эллипса
![]() .
.
Задача 55.
Составить уравнение прямой, проходящей
через правый фокус и верхнюю вершину
эллипса
![]() .
.
Задача 56*.
На эллипсе
![]() найти точку, расстояние которой от
правого фокуса в два раза меньше чем её
расстояние от левого фокуса.
найти точку, расстояние которой от
правого фокуса в два раза меньше чем её
расстояние от левого фокуса.
Задача 57*.
Дан эллипс
![]() и окружность, имеющая центр в верхней
вершине малой оси эллипса и проходящая
через его фокусы. Найти точки пересечения
эллипса и окружности.
и окружность, имеющая центр в верхней
вершине малой оси эллипса и проходящая
через его фокусы. Найти точки пересечения
эллипса и окружности.
Гипербола
Гиперболой
называется
геометрическое место точек плоскости,
модуль разности расстояний, которых от
двух фиксированных точек, называемых
фокусами гиперболы, есть величина
постоянная (![]() ),
меньшая чем расстояние между фокусами
(
),
меньшая чем расстояние между фокусами
(![]() )
(Рис. 11).
)
(Рис. 11).
П ростейшее
(каноническое) уравнение гиперболы мы
получим, если выберем прямую, соединяющую
фокусы, за ось абсцисс и поместим начало
координат в середине между ними. Тогда
уравнение гиперболы примет вид:
ростейшее
(каноническое) уравнение гиперболы мы
получим, если выберем прямую, соединяющую
фокусы, за ось абсцисс и поместим начало
координат в середине между ними. Тогда
уравнение гиперболы примет вид:
![]() ,
(21)
,
(21)
где
![]() .
(22)
.
(22)
Точки
![]() ,
,![]() ,
пересечения эллипса с осью называютсявершинами
гиперболы. Отрезок
,
пересечения эллипса с осью называютсявершинами
гиперболы. Отрезок
![]() называетсядействительной
осью гиперболы,
отрезок
называетсядействительной
осью гиперболы,
отрезок
![]() называетсямнимой
осью гиперболы,
параметры
называетсямнимой
осью гиперболы,
параметры
![]() и
и![]() ,
входящие уравнение (21), называютсядействительной
и мнимой полуосями соответственно.
,
входящие уравнение (21), называютсядействительной
и мнимой полуосями соответственно.
Гиперболы
![]() и
и ![]() ,
,
называется сопряжёнными.
Если
![]() ,
то гипербола называетсяравносторонней.
,
то гипербола называетсяравносторонней.
Эксцентриситетом гиперболы называется отношение расстояния между фокусами к его большой оси, т. е.
![]() .
(23)
.
(23)
Очевидно, что
![]() .
.
Гипербола (24)
состоит из двух бесконечных ветвей
(правой и левой). Расстояние точки
![]() гиперболы от его фокусов (фокальные
радиус-векторы)
определяются формулами:
гиперболы от его фокусов (фокальные
радиус-векторы)
определяются формулами:
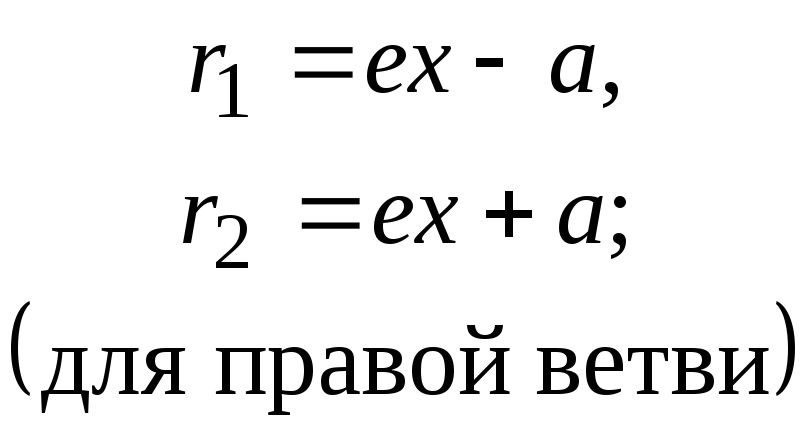

Директрисами
эллипса называются две прямые,
перпендикулярные большой оси эллипса
и отстоящие от его центра на расстоянии,
равном
![]() .
Уравнения директрис:
.
Уравнения директрис:
![]() ,
, ![]() . (24)
. (24)
Прямые
![]() называютсяасимптотами
гиперболы.
называютсяасимптотами
гиперболы.
Задача 58.
Составить каноническое уравнение
гиперболы, зная, что уравнения асимптот
![]() и расстояние между директрисами
и расстояние между директрисами![]() .
.
Решение. Каноническое уравнение гиперболы (21):
![]() .
.
Для того чтобы
найти параметры
![]() и
и![]() составим систему.
составим систему.
Известно, что асимптоты гиперболы задаются уравнениями
![]() .
.
Тогда из условия задачи получим первое уравнение системы:
![]() .
.
Так как уравнения директрис (24):
![]() ,
, ![]() ,
,
то из условия задачи
![]() .
.
Из равенств (22) и (23) следует, что
![]() .
.
Тогда
![]() .
.
Это второе уравнение системы.
Итак, получили систему

Её решение
![]() ,
,![]() .
.
Искомое уравнение гиперболы
![]() .
.
Задача 59.
Фокусы гиперболы совпадают с фокусами
эллипса
![]() .
Составить уравнение гиперболе, если её
эксцентриситет равен 2.
.
Составить уравнение гиперболе, если её
эксцентриситет равен 2.
Решение. Из канонического уравнения данного эллипса известно, что
![]() ,
,
![]() .
.
По формуле (16)
найдём
![]() :
:
![]() .
.
По условию задачи фокусы гиперболы совпадают с фокусами эллипса. Значит
![]() .
.
Так как эксцентриситет гиперболы равен 2, то
![]() .
.
Для нахождения
![]() воспользуемся равенством (22):
воспользуемся равенством (22):
![]() .
.
Следовательно, искомое уравнение гиперболы
![]() .
.
Задачи для самостоятельного решения
Задача 60. Найти координаты полуоси, фокусы, эксцентриситет, уравнения асимптот и уравнения директрис данных гипербол:
|
1)
|
3)
|
|
2)
|
4)
|
Задача 61. Составить каноническое уравнение гиперболы, зная, что:
её вещественная ось равна 10, а мнимая 8;
расстояние между фокусами равно 10, а мнимая ось 8;
расстояние между фокусами равно 6, и эксцентриситет равен
 ;
;действительная ось равна 16, эксцентриситет равен
 ;
;уравнения асимптот
 и расстояние между фокусами равно 20;
и расстояние между фокусами равно 20;расстояние между директрисами равно
 ,
а мнимая ось равна 6;
,
а мнимая ось равна 6;расстояние между директрисами равно
 ,
эксцентриситет
,
эксцентриситет ;
;точки
 и
и принадлежит гиперболе;
принадлежит гиперболе;точка
 принадлежит гиперболе и эксцентриситет
принадлежит гиперболе и эксцентриситет ;
;точка
 принадлежит гиперболе и уравнения
асимптот
принадлежит гиперболе и уравнения
асимптот ;
;расстояние между директрисами равно
 ,
расстояние между фокусами 26;
,
расстояние между фокусами 26;уравнения асимптот
 и уравнения директрис
и уравнения директрис .
.
Задача 62. Найти эксцентриситет равносторонней гиперболы.
Задача 63.
Составить уравнение гиперболы, имеющей
вершины в фокусах, а фокусы![]() в
вершинах эллипса
в
вершинах эллипса![]() .
.
Задача 64.
Составить уравнение гиперболы, фокусы
которой лежат в вершинах эллипса
![]() ,
а директрисы проходят через фокусы
этого эллипса.
,
а директрисы проходят через фокусы
этого эллипса.
Задача 65.
Составить уравнение гиперболы, фокусы
которой лежат в фокусах эллипса
![]() ,
а её эксцентриситет равен 1,2.
,
а её эксцентриситет равен 1,2.
Задача 66.
Через точку
![]() провести прямые, параллельные асимптотам
гиперболы
провести прямые, параллельные асимптотам
гиперболы![]() .
.
Задача 67.
Определить острый угол между асимптотами
гиперболы
![]() .
.
Задача 68.
Найти точки пересечения гиперболы
![]() с прямыми:
с прямыми:
1)
![]() ;
;
2)
![]() ;
;
3)
![]() .
.
Задача 69.
Найти точки пересечения гиперболы
![]() и окружности
и окружности![]() .
.
Задача 70*.
Дана гипербола
![]() .
Найти софокусную гиперболу, проходящую
через точку
.
Найти софокусную гиперболу, проходящую
через точку![]() .
.
Парабола
Параболой называется геометрическое место точек плоскости, равноудалённых от данной точки, называемой фокусом, и данной прямой, называемой директрисой параболы.
Величина
![]() ,
равная расстоянию от фокуса до директрисы,
называетсяпараметром
параболы. Прямая, проходящая через фокус
перпендикулярно директрисе, называется
осью
параболы. Точка пересечения параболы
с её осью называется вершиной.
,
равная расстоянию от фокуса до директрисы,
называетсяпараметром
параболы. Прямая, проходящая через фокус
перпендикулярно директрисе, называется
осью
параболы. Точка пересечения параболы
с её осью называется вершиной.
|
|
|
Если ось параболы выбрать в качестве одной из осей координат, а вторую ось провести посередине между фокусом и директрисой, то мы получим простейшее уравнение параболы. В зависимости от выбора осей получим одно из следующих уравнений:
![]() (Рис.12) (25)
(Рис.12) (25)
![]() (Рис.13) (26)
(Рис.13) (26)
![]() (Рис.14) (27)
(Рис.14) (27)
![]() (Рис.15) (28)
(Рис.15) (28)
|
|
|
Уравнения (25)-(28) называются каноническими уравнениями параболы.
Фокальный
радиус-вектор произвольной точки
![]() параболы (25) (т.е. длина отрезка
параболы (25) (т.е. длина отрезка![]() )
вычисляется по формуле
)
вычисляется по формуле
![]() (29)
(29)
(аналогичные формулы можно получить для парабол, заданных уравнениями (26)-(28)).
Задача 71.
На параболе
![]() найти точки, фокальный радиус которых
равен 13.
найти точки, фокальный радиус которых
равен 13.
Решение.
Пусть
![]() искомая
точка. Из уравнения параболы
искомая
точка. Из уравнения параболы
![]() .
.
Из условия задачи фокальный радиус
![]() .
.
Подставим в формулу
(29):
![]() .
.
Подставим координаты
точки
![]() в уравнение параболы и найдём вторую
координату:
в уравнение параболы и найдём вторую
координату:
![]() .
.
Таким образом,
![]() .
.
Задачи для самостоятельного решения
Задача 72. Составить уравнение параболы, вершина которой находится в начале координат, зная, что:
парабола расположена в правой полуплоскости симметрично относительно оси
 ,
и её параметр равен 3;
,
и её параметр равен 3;парабола расположена в левой полуплоскости симметрично относительно оси
 ,
и её параметр равен 0,5;
,
и её параметр равен 0,5;парабола расположена в верхней полуплоскости симметрично относительно оси
 ,
и её параметр равен 2;
,
и её параметр равен 2;парабола расположена в нижней полуплоскости симметрично относительно оси
 ,
и её параметр равен 1;
,
и её параметр равен 1;парабола расположена симметрично относительно оси
 и проходит через точку
и проходит через точку ;
;парабола расположена симметрично относительно оси
 и проходит через точку
и проходит через точку ;
;парабола расположена симметрично относительно оси
 и проходит через точку
и проходит через точку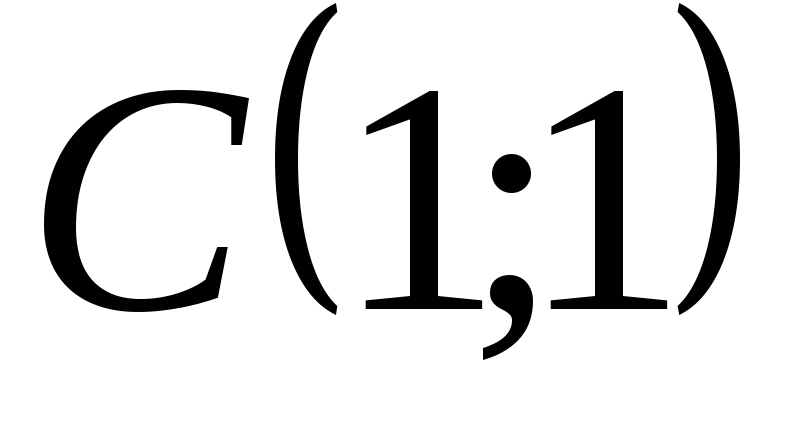 ;
;парабола расположена симметрично относительно оси
 и проходит через точку
и проходит через точку ;
;фокус параболы
 ;
;фокус параболы
 ;
;директриса параболы
 ;
;директриса параболы
 .
.
Задача 73. Найти фокус и уравнение директрисы параболы:
|
1)
|
2)
|
3)
|
4)
|
Задача 74.
На параболе
![]() найти точки, расстояния которых до
фокуса равны 34.
найти точки, расстояния которых до
фокуса равны 34.
Задача 75.
На параболе
![]() найти точки, расстояния которых до
фокуса равны 4,5.
найти точки, расстояния которых до
фокуса равны 4,5.
Задача 76.
Составить уравнение прямой, проходящей
через фокус параболы
![]() под углом
под углом![]() к оси
к оси![]() .
.
Задача 77.
Через фокус параболы
![]() проведена хорда, перпендикулярная к её
оси. Найти длину этой хорды.
проведена хорда, перпендикулярная к её
оси. Найти длину этой хорды.
Задача 78.
Найти точки пересечения параболы
![]() и прямой, если:
и прямой, если:
1)
![]() ;
2)
;
2)![]() ;
3)
;
3)![]() ;
4)
;
4)![]() .
.
Задача 79.
Найти точки пересечения параболы
![]() и эллипса
и эллипса![]() .
.
Задача 80.
Найти точки пересечения параболы
![]() и гиперболы
и гиперболы![]() .
.
Задача 81.
Через фокус параболы
![]() проведена прямая, параллельная прямой
проведена прямая, параллельная прямой![]() .
найти длину образовавшейся хорды.
.
найти длину образовавшейся хорды.
Задача 82. Написать уравнение окружности, имеющей центр в фокусе параболы и касающейся её директрисы, если парабола задана уравнением:
1)
![]() ; 2)
; 2)![]()
ОТВЕТЫ
§ 1
5. 1)
![]() ,
,![]() ;
2)
;
2)![]() ,
,![]() .
7.1)
.
7.1)
![]() ;2)
;2)
![]() .
8. 1)
.
8. 1)
![]() ,
,![]() ;
2)
;
2)![]() ,
,![]() .
9, 1)
.
9, 1)
![]() ,
,![]() ,
2)
,
2)![]() ,
,![]() .
10. 1)
.
10. 1)
![]()
![]() ;
2)
;
2)
![]() ,
,![]() ,
,![]() .
11.1)
.
11.1)
![]() ,
,![]() ;
2)
;
2)![]() ,
,
![]() .
12.9 кв.ед.
14.
.
12.9 кв.ед.
14.
![]() .
15.
.
15.![]() ,
,![]() .
.
§ 2
21.
1)
![]() ;
2)
;
2)![]() ;
3)
;
3)![]() .
22. 1)
.
22. 1)
![]() ;
2)
;
2)![]() .
23.
.
23.
![]() ,
,![]() ,
,![]() .
24.
.
24.![]() ,
,![]() ,
,![]() ,
,![]() .
25.
.
25.![]() .
26.1)
20 кв.ед.; 2) 4.8 кв.ед.
27. 1)
.
26.1)
20 кв.ед.; 2) 4.8 кв.ед.
27. 1)
![]() ,
,![]() ;
2)
;
2)![]() ,
,![]() .28.
1)
.28.
1)
![]() ,
2)
,
2)![]() .
29. 1)
.
29. 1)
![]() ,
,![]() ,
,![]() ;
2)
;
2)
![]() ,
,![]() ,
,![]() .
30.
.
30.![]() ,
,![]() ,
,![]() .
31.1)
.
31.1)
![]() ,
,![]() ;
2)
;
2)
![]() ,
,![]() .
32.
1)
.
32.
1)
![]() ,
2)
,
2)![]() 3)
3)![]() .
33. 1)
2.8 ед., 0 ед.;
2) 1 ед.,
2 ед.
34.
1)
.
33. 1)
2.8 ед., 0 ед.;
2) 1 ед.,
2 ед.
34.
1)
![]() ;
2)
;
2)
![]() 35.1)
35.1)
![]() ;
2) 1.
36. 1)
;
2) 1.
36. 1)
![]() ,
,![]() ;
2)
;
2)
![]() ,
,![]() .
37.1)
.
37.1)
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ;
2)
;
2)![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
38.
.
38.
![]() ,
,![]() ,
,![]() ,
39.
,
39.![]() .
40.
.
40.![]() .
.
§3
42. 1)
![]() ;
2)
;
2)![]() ;
3)
;
3)![]() ;
4)
;
4)![]() ;
5)
;
5)![]() ;
6)
;
6)![]() ,
,![]() .
43. 1)
.
43. 1)
![]() ,
,![]() ;
2)
;
2)![]() ,
,![]() ;
3)
;
3)![]() ,
,![]() ,
4)
,
4)![]() ,
,![]() ;
5)
;
5)
![]() ,
,![]() .
44.1)
.
44.1)
![]() ,
,![]() ;
2) нет общих точек; 3) прямая касается
окружности в точке
;
2) нет общих точек; 3) прямая касается
окружности в точке![]() .
45.
.
45.
![]() .
46.1)
.
46.1)
![]() ;
2)
;
2)
![]() .
49.1)
.
49.1)
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ;
2)
;
2)![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ;
3)
;
3)![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ;
4)
;
4)![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
50.
1)
.
50.
1)
![]() ;
2)
;
2)![]() ;
3)
;
3)![]() ;
4)
;
4)![]() ;
5)
;
5)![]() ;
6)
;
6)![]() ;
7)
;
7)![]() ;
8)
;
8)![]() ;
9)
;
9)![]() или
или![]() ;
10)
;
10)![]() ;
11)
;
11)![]() ;
12)
;
12)![]() .51.
.51.
![]() .
52.
.
52.![]() .
53.1)
.
53.1)
![]() ;
2)
;
2)![]() . 54.
. 54.
![]() .
55.
.
55.![]() .
56.
.
56.![]() .
57.
.
57.![]() .
60.1)
.
60.1)
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ;
2)
;
2)![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ;
3)
;
3)![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ;
4)
;
4)
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ;
61.1)
;
61.1)
![]() ;
2)
;
2)![]() ;
3)
;
3)![]() ;
4)
;
4)![]() ;
5)
;
5)![]() ;
6)
;
6)![]() ;
7)
;
7)![]() ;
8)
;
8)![]() ;
9)
;
9)![]() ;
10)
;
10)![]() ;
11)
;
11)![]() ;
12)
;
12)![]() .62.
.62.
![]() .
63.
.
63.
![]() ;64.
;64.
![]() .65.
.65.
![]() .66.
.66.
![]() ,
,![]() .
67.
.
67.![]() .
68.1)
.
68.1)
![]() ,
,![]() ;
2) прямая касается гиперболы в точке
;
2) прямая касается гиперболы в точке
![]() ;
3) точек
пересечения нет.
69.
;
3) точек
пересечения нет.
69.
![]() ,
,![]() ,
,![]() ,
,![]() .
70.
.
70.
![]() .72. 1)
.72. 1)
![]() ;
2)
;
2)![]() ;
3)
;
3)![]() ;
4)
;
4)![]() ;
5)
;
5)![]() ;
6)
;
6)![]() ;
7)
;
7)![]() ;
8)
;
8)![]() ;
9)
;
9)![]() ;
10)
;
10)![]() ;
11)
;
11)![]() ;
12)
;
12)
![]() .
73.1)
.
73.1)
![]() ,
,![]() ;
2)
;
2)![]() ,
,![]() ;
3)
;
3)![]() ,
,![]() ;
4)
;
4)![]() ,
,
![]() .
74.
.
74.![]() .
75.
.
75.![]() .
76.
.
76.![]() .
77.16.
78. 1)
.
77.16.
78. 1)
![]() ,
,![]() ;
2) прямая касается параболы в точке
;
2) прямая касается параболы в точке![]() ;
3) точек пересечения нет; 4)
;
3) точек пересечения нет; 4)
![]() ,прямая
параллельна оси параболы.
79.
,прямая
параллельна оси параболы.
79.
![]() .
80.
.
80.![]() ,
,![]() .
81.64.
82. 1)
.
81.64.
82. 1)
![]() ;
2)
;
2)![]() .
.
СПИСОК ЛИТЕРАТУРЫ
Баврин, И. И. Высшая математика. – М. /И. И. Баврин: Академия, 2004. – 616 с.
Ьугров, Я. С и др. Высшая математика. – М. /Я. С. Бугров и др.: Дрофа, 2004. т.3. – 512 с.
Данко, П. Е. и др. Высшая математика в упражнениях и задачах. – М. /П. Е. Данко: Высшая школа,2000.
 304 с.
304 с.Каплан, И. А. Практические занятия по высшей математике. – Харьков. /Изд. Харьковского гос. ун-та, 1967. – 948 с.
Минорский, В. П. Сборник задач по высшей математике.
 М. /В. П. Минорский: Наука, 1969.
М. /В. П. Минорский: Наука, 1969. 352
с.
352
с.Письменный, Д. Т. Конспект лекций по высшей математике. Полный курс. – М. /Д. Т. Письменный: АЙРИС ПРЕСС, 2007г.
Шипачев, В. С. Высшая математика. – М. /В. С. Шипачев: Высшая школа, 1990.
 480 с.
480 с.Шипачев, В. С. Задачник по высшей математике. – М. /В. С. Шипачев: Высшая школа, 2008.
 304 с.
304 с.
Методические указания по
«Высшей математике» раздел «Аналитическая геометрия на плоскости»
для студентов I курса дневной формы обучения направления 6.040101 «химия»
образовательно-квалификационного уровня «бакалавр» отрасли знаний 0401 «Естественные науки»
Составители: Корнута Анжелика Александровна,
Плышевская Светлана Петровна.
Редактор: Н. А. Василенко
______________________________________________________________
Подписано к печати 4. 06. 09 . Формат 60x84/16. Бумага тип. ОП. Объем 1,5 п. л. Тираж - 50. Заказ-
_______________________________________________________________
95007, Симферополь, пр. Академика Вернадского, 4. Таврический национальный университет им. В. И. Вернадского.




