Фх / Фх / ТЕРМОДИНАМІКа ПАРИ

ЕЛЕМЕНТИ ТЕРМОДИНАМІКИ ПАРИ

План лекції №

1 Метод діаграм. Р — Vдіаграма води

2 Характеристика вогкої й сухої пари.

Термодинамічні розрахунки реальних систем стали можливими лише після появи роботи Гіббса (1873), в якій викладені принципи розробленого їм методу діаграм в термодинамічних дослідженнях. Стаття Гіббса викликала величезний інтерес у дослідників. Видатний учений того часу Максвел дав їй високу оцінку і на знак вдячності послав молодому автору гіпсову об'ємну модель діаграми стану, яка і понині зберігається в університетському музеї м. Йеля (США) на батьківщині Гіббса.

Метод діаграм винятковий по своїй простоті і наочності і повністю відшкодовує відсутність рівняння стану. Тому його використовують як в теоретичних дослідженнях, так і в практичній діяльності. При вивченні оборотних термодинамічних процесів ідеального газу використовуються

Р—V- і Т—S- діаграми для наочної ілюстрації процесів, що вивчаються. Для розрахунку процесів за участю ідеального газу, а також повітря і деяких легких газів (азот, водень, гелій, кисень і т. п.) при

Р < 10⁷ Па і Т > 0°С немає особливої необхідності в діаграмі стану, оскільки для них є вельми просте рівняння стану, дійсне у вказаних умовах. Але навіть перераховані гази в умовах, близьких до критичних, не підкоряються рівнянню стану ідеального газу, не говорячи вже про рідини і тверді тіла. У останньому випадку термодинамічні розрахунки можна проводити лише за допомогою діаграм стану, побудованих на підставі експериментальних даних.

Р — V діаграма звичайних речовин (води)

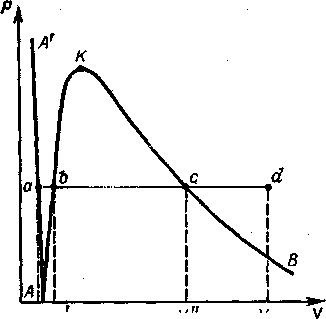
Рисунок - До термодинаміки ізобаричного пароутворення

Процеси за участю звичайних речовин мають деякі особливості, що відрізняють їх від ідеальних газів. Це пов'язано з тим, що звичайні речовини можуть знаходитися в твердому, рідкому і газоподібному агрегатних станах.

Внаслідок цього процеси звичайних речовин нерідко супроводжуються фазовими переходами: плавленням, кипінням, конденсацією і т.п.

Як приклад розглянемо процес ізобаричного розширення води. Для спрощення приймемо незалежність від Т і Р питомого об'єму рідкої води і нехтуватимемо його значенням порівняно зі значенням питомого об'єму газоподібної води— водяної пари, а значення U, Н і S води при 0°С приймемо рівними нулю.

Більшість технологічних процесів протікають при Р = const, тому розглянемо ізобаричний процес.

Графік оборотного ізобаричного процесу на Р — V-діаграмі має вид прямої, паралельної осі V, незалежно від природи даної системи (пряма ad).

Процес складається з трьох основних стадій:

1 - нагрівання рідини до температури кипіння — t_кип (ділянка ab),

2 - википання рідини з утворенням сухої насиченої пари (ділянка bс)

3 - нагрівання пари до температури перегріву — t_пер з утворенням перегрітої пари (ділянка cd).

Допустимо, що точка а розташована на ізотермі А А', відповідної t = 0°С.

Тоді U, Н і S даної системи (1кг Н₂О) в початковому стані рівні нулю.

Під час переходу системи до кипіння (точка b) температура її підвищується до t_кип, тобто змінюється на: t = t_кип - t⁰

Якщо врахувати, що об'єм рідини на цій стадії процесу залишається практично постійним, то для теплоти і роботи процесу справедливі співвідношення Q_ab = q' = с ^. t_кип і W_ab = Р V_аb = 0.

На наступній стадії процесу (ділянка bc) вода починає випаровуватись. Об’єм системи збільшується, а температура її залишається постійною: t_кип = t_нас, де t _нас – температура насичення пари. Теплота процесу дорівнює питомій теплоті пароутворення, а робота процесу дорівнює роботі розширення.

На стадії, відповідній ділянці графіку сd, пара ізобарично розширюється в результаті підвищення температури. Так утворюється пара, яка називається перегрітою.

Точка d характеризує звичайно газуватий стан речовини. При утворенні перегрітої пари температура системи підвищується до t_пер, тобто перевищує t_нас , а об’єм зростає доV_пер .

Зміни функцій стану системи в процесі отримання 1кг перегрітої пари з 1 кг рідкої води, взятої за температури 0⁰С (лінія аd):

теплота процесу: Q_ab = Q_пер

робота процесу: W_ab = РV_пер

зміна ентальпії: Н = Q_пер

зміна внутрішньої енергії: U_ab = Q_пер – Р V_пер

зміна ентропії:

S = 2,303с' lg[(273 + t_кип) / 273] + q_вип / (273 + t_кип) + 2,303c'' lg [(273 + t_пер) / (273 + t_нас)]

Волога пара

При охолоджуванні перегрітої пари стадії її утворення чергуються в зворотній послідовності: з перегрітої пари при зниженні її температури до t_нас утворюється суха насичена пара, потім пара конденсується в рідину при t_нас = t_кип і, нарешті, вода охолоджується до 0°С. Але процес цей має характерну особливість, а саме: утворенню рідкого конденсату передує утворення туману.

Туман — це сукупність найдрібніших крапельок рідини, що знаходяться в зваженому стані в об'ємі сухої насиченої пари. У технологічній практиці такий туман прийнято називати вологою парою.

Для характеристики його окрім розглянутих раніше параметрів стану (Т, Р, V° і ін.) вводиться ще один параметр — ступінь сухості.

Ступенем сухості пари називається масова частка сухої насиченої пари, що міститься у вологій парі

X = m_п / (m_п + m_р )

де m_п і m_р — маси сухої насиченої пари і краплинної рідини у вологій парі.

Для ступеня сухості пари справедливо: 0 < X < 1.

При X = 0 вода знаходиться в стані закипілої рідини, а при X = 1 — в стані сухої насиченої пари. Точки на діаграмі, що характеризують пару з однаковими ступенями сухості, складають лінії, витікаючи з крапки К, відповідної критичному стану води. Ці криві називаються лініями постійності ступеня сухості пари. Виділяються верхня та нижня граничні криві (лінії постійності ступеня сухості пари).

Поняття ступеня сухості пари дозволяє зручно проводити теплотехнічні розрахунки, пов'язані з утворенням вологої пари.

План лекції №

1 T – S діаграма повітря і води

2 H – S діаграма повітря і води

Т — S діаграма повітря

Переваги Р—V-дiаграм стану речовини — наочність і можливість графічного визначення роботи процесу. Але в технологічній практиці основна увага приділяється визначенню теплоти процесу, особливо при розрахунках теплопередачі, а Р—V-дiаграма не дозволяє зробити це безпосередньо.

У технічних розрахунках, пов'язаних з використанням як робочого тіла азоту або повітря, успішно використовується Т — S діаграма ідеального газу.

З її допомогою можна проводити термодинамічні розрахунки процесів, в результаті яких температура робочого тіла (повітря) змінюється від — 50 °С до 350 °С, а тиск — від 10⁵ Па до 10⁷ Па.

Для зручності на діаграму нанесені сітки ізотерм, адіабат, ізобар і ізохор. Ізотерми і адіабати розташовані паралельно осям координат. На вісь Т нанесена температурна шкала в °С або К.

На вісь S немає необхідності наносити значення ентропії, оскільки визначення абсолютного значення її для повітря складне, так і немає в цьому необхідності, оскільки в розрахунках звичайно використовують зміни ентропії, що відбуваються в результаті даного процесу. Визначити зміну ентропії повітря в якому-небудь процесі можна, скориставшись масштабною лінійкою, що додається.

Приклад.

Визначити роботу, виконану тепловою машиною Карно за один цикл, якщо температура нагрівача (джерела теплоти) 300 °С, температура холодильника (приймача теплоти) 0°С, а зміна ентропії відповідає довжині відрізка осі в 250 мм.

Рішення.

Робота теплової машини Карно дорівнює

W(Q) = (T₁ – T₂) S

Зміна температури робочого тіла по умові завдання складає

(Т₁ - Т₂) = (t₁ - t₂) = 300 - 0 = 300 K

Для визначення S слід скористатися маштабной лінійкою.

1мм цієї лінійки відповідає зміні ентропії на 4,184 Дж/(кг^.К).

Знаючи масштаб осі, розрахуємо зміну S, відповідну довжині відрізка осі в 250 мм:

S = 250 мм ^. 4,184 Дж/(кг^.К^.мм) = 1046 Дж/(кг^.К)

Використовуючи одержані дані, визначимо роботу

W(Q) = 300К ^. 1046 Дж/(кг^.К) = 313,8 кДж/кг

Ізобари і ізохори на Т — S-діаграмі ідеального газу мають форму логарифмічних кривих.

Причому ізохори зігнуті до осі Т крутіше, ніж ізобари, оскільки С_р > С_V. На робочій діаграмі повітря ізобари нанесені суцільними, а ізохори штриховими логарифмічними кривими.

Для зручності ведення розрахунків на них нанесені відповідні їм значення тиску і питомих об'ємів.

Оскільки будь-яка точка діаграми — це графічне зображення деякого стану системи, остільки значення Р, Т і V характеризують ізобару, ізотерму і ізохору, що проходять через точку, що описує стан системи.

Наприклад, значення цих функцій для повітря, стан якого зображено точкою *, рівні: 45^.10⁵Па, 200°С

і 0,03 м³/кг.

Якщо крапка, що зображає на діаграмі стан системи, не співпадає з кривою, то значення відповідного параметра стану системи визначається графічною інтерполяцією.

350

0 50 100 150 200 250 300 350 400

30 25 20 16 12 10 3,0 6,0 5,04,0 3.0 2,5 2,0 1,6 1,2 1,0 Р,Па 10 ^-5

Рисунок - Т—S Діаграма повітря

Приклад

Для повітря при 200 °С Р = 6^.10⁶ Па. Визначити густину повітря в даних умовах.

Рішення.

Густина речовини дорівнює зворотному значенню його питомого об'єму: ρ = 1/V.

Отже, рішення задачі зводиться до визначення V по Т—S діаграмі.

По значеннях Т і Р знаходимо на Т—S-діаграмі точку П .

На кресленні ізохора, що перетинає дану крапку, не нанесена; вона повинна проходити приблизно посередині між ізохорами v = 0,020 і 0,025 м³/кг. Отже, значення V приблизно дорівнює

V = (0,020 + 0,025)/2 = 0,022 м³/кг, а ρ = 1/ 0,022 = 45,4 кг/м³

Т — S-діаграма води

На практиці як робоче тіло теплових машин, а також теплоносія в теплообмінниках використовують речовини, що значно відрізняються від ідеального газу. Звичайно це речовини, що мають велику теплоємність і, отже, високу критичну температуру. З цієї причини експлуатація подібних речовин протікає в тій області станів, де вони різко відрізняються від ідеального газу.

Розглянемо термодинамічні процеси таких речовин на Т—S-діаграмі.

Подібно тому, як це було у разі Р— V діаграми, на Т—S-діаграмі можна виділити області:

- рідкого стану (МКА);

- фазового переходу (під прикордонними кривими АК і KB)

- газоподібного стану (вище і правіше за лінію МКВ).

Ізотерми і адіабати, будучи паралельними відповідним осям координат і незалежними від природи речовини системи і його агрегатного стану, не представляють особливого інтересу. Тому розглянемо тільки ізобари і ізохори.

Процес ізобаричного пароутворення зображується на Т—S діаграмі лінією abсd.

Ділянка ab відповідає розігріванню води від 0°С до t_кип; ентропія, відповідно, збільшується від s° до s'. Теплота цього процесу дорівнює Q_ab = с' t_кип = TdS = S_0abs'

Теплота може бути приблизно визначена і графічно в допущенні, що ізобара на даній ділянці лінійна. Тоді фігура 0abs' може бути представлена трапецією з висотою s' — s° = s' і основою Ta і Тb.

0 s' S_кр f e s'' S_пер S

Рисунок - T—S-Діаграма води

Ділянка bс відповідає ізобаричному кипінню: температура системи залишається постійною

(t_кип = t_нac), а ентропія зростає від s' до s".

Ділянка cd відповідає ізобаричному перегріву пари; температура пари підвищується від t_нас до t_пер,

а ентропія, відповідно, збільшується від s" до s_nep. Теплота цієї стадії процесу може бути так само приблизно визначена графічно.

Як випливає з рисунка , ізобари на Т — S-діаграмі води подібні ізобарам Т — S-діаграми повітря. Відмінність полягає лише в тому, що на першій є перехідна область, обмежена кривими АК і КВ.

Крім того, необхідно відзначити також, що ізобари на Т — S-діаграмі води як би збираються в пучок на початку координат і розходяться віялом у міру видалення від нього.

Ізохори на Т — S-діаграмі води так само збираються в пучок на початку координат і так само, як ізобари, розходяться віялом. Відмінність їх полягає лише в тому, що ізохори проходять крутіше, ніж ізобари (штрихові лінії на рисунку зображають ізохори, а суцільні — ізобари). Така відмінність обумовлена тим, що теплота ізобаричного процесу більше теплоти ізохоричного процесу, що протікає в тому ж інтервалі температур.

Характерною особливістю Т — S-діаграми ідеального газу (повітря) була еквідистантность ізобар і ізохор, яка виражалася в збереженні постійної відстані (дистанції) між найближчими ізобарами і ізохорами на всьому протязі їх розташування.

На Т — S-діаграмі води це явище відсутнє — криві розходяться віялом у міру видалення від початку координат. Але необхідно відзначити, що у міру видалення вказаних кривих від верхньої прикордонної кривої в глибину області перегрітої пари еквидистантность їх поступово починає виявлятися. Це явище указує на наближення властивостей водяної пари (так само і інших речовин), при достатньому підвищенні їх температури до властивостей ідеального газу.

Н— S-діаграма

Р—V- і Т—S-Діаграми використовують в основному в теоретичних дослідженнях.

Для практичних цілей ці діаграми мало придатні, оскільки для визначення енергетики (теплоти і роботи), що супроводжують досліджувані процеси, необхідно проводити на діаграмах відповідні планіметричні вимірювання, що нерідко є досить трудомісткою операцією. Тоді ж, коли виникає необхідність визначення зміни внутрішньої енергії або ентальпії системи ці діаграми виявляються абсолютно даремними. Внутрішня енергія і ентальпія ідеального газу є однозначними функціями температури. Використовуючи цю залежність, можна побудувати U—S- і Н—S- діаграми стану, аналогічні Т—S діаграмі. Оскільки ентальпія більш повно характеризує термодинамічну систему, ніж внутрішня енергія, на практиці частіше застосовують Н—S-діаграму. Теплоту або роботу визначають в даному випадку по довжинах відрізків на осях Н і S.

Н — S- діаграма води

На Н—S-діаграмі (рисунок ) слід виділити три області станів:

- рідкого - МКА;

- перехідної або вологої пари — під прикордонними кривими

- газоподібної або перегрітої пари — над лінією МКВ.

Для зручності на діаграму нанесені прикордонні криві, ізотерми, ізобари, адіабати, ізоентальпи, а так само ступені сухості пари (під прикордонними кривими).

На всіх цих лініях дані відповідні характеристики.

Ізоентальпи і адіабати паралельні відповідним осям координат і на них зупинятися немає необхідності.

Ізобари на Н—S діаграмі води у області рідкого стану мають форму логарифмічних кривих, зігнутих у бік осі Н. Це пояснюється логарифмічною залежністю ентропії системи і невеликим збільшенням теплоємності води при підвищенні температури.

У області вологої пари ізобари лінійні. Кут нахилу їх відповідає Т_кип, постійної за Р = const:

Це відповідає також і постійності питомої теплоти паротворення при Р = const.

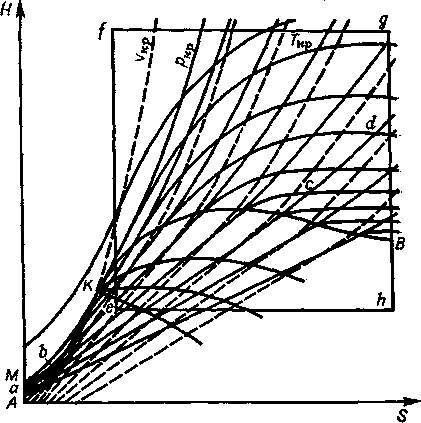
Рисунок - H — S діаграма води

У області перегрітої пари ізобари мають яскраво виражену форму логарифмічних кривих із-за наявності і в цьому випадку логарифмічної залежності ентропії системи від температури.

Слід проте відзначити, що значний вплив на форму ізобар надає в цій області температурна залежність теплоємності водяної пари.

Ізохори на Н — S-діаграмі води так само, як і на Т — S-діаграмі, проходять крутіше, ніж ізобари, і мають форму логарифмічних кривих, зігнутих у бік осі Н.

Як ізобари, так і ізохори збираються в пучок поблизу початку координат: місце «концентрації» ізобар знаходиться вищим за місце концентрації ізохор. У міру видалення від початку координат в область перегрітої пари ізобари і ізохори розходяться віялом і поступово набувають еквидистантність, характерну для ідеального газу, що указує на наближення властивостей водяної пари до властивостей ідеального газу.

Ізотерми на Н—S діаграмі води мають S-образну форму і для температур, нижче критичної; на їх з'являються лінійні ділянки, що зливаються з ізобарами при перетині ними області вологої пари.

Над нижньою прикордонною кривою (у області рідкого стану речовини і вище) ізотерми зігнуті вгору до осі Н і проходять небагато пологіше, чим ізобари, тому останні перетинають їх від низу до верху.

Над верхньою прикордонною кривою ізотерми зігнуті в протилежну сторону — до осі S і у міру видалення від верхньої прикордонної кривої стають паралельними осі S. Це прагнення ізотерм при видаленні углиб області перегрітої пари прийняти форму ізоентальп вказує на наближення властивостей водяної пари до властивості ідеального газу.

У технологічній практиці процеси часто йдуть з утворенням вологої пари. Тому на Н—S-діаграму наносять ще і лінії постійності ступеня сухості пари, по яких визначають термодинамічний стан вологої пари. На рисунку вони виділяються тим, що виходять з критичної точки К.

На виробництві звичайно мають справу з перегрітою і вологою парою. Отже, практичну цінність представляє лише та частина Н—S-діаграми води, яка описує стан перегрітої і вологої пари.

На рисунку ця частина діаграми виділена прямокутником efgh.

На рисунку вона приведена окремо як Н — S-діаграма водяної пари.

Приклад

Температура куба нафтоперегінної установки низького тиску 300 °С. Визначити витрату пари, якщо температура підтримується за рахунок ізотермічного розширення (у теплообміннику установки) перегрітої пари, початковий тиск якої 4,5^.10⁶, а кінцевий — 2^.10⁵ Па.

Потужність установки Ф = 250 кВт, к. к. д. = 0,6.

Рішення.

По умові завдання пар зазнає в теплообміннику ізотермічне розширення. Отже, рішення задачі зводиться до визначення теплоти ізотермічного процесу: Q = Т S.

На H—S діаграмі водяної пари знаходимо точки початкового і кінцевого станів пари.

Вони розташовані на перетині ізотерми 300 °С з ізобарами 4,5^.10⁶ Па (вихідний стан) і 2^.10⁵ Па (кінцевий стан). Проектуючи ці крапки на вісь S, знаходимо значення ентропії пари: s₁ = 6,29 і

s₂ = 7,89 кДж/(кг^.К). Використовуючи одержані дані, розраховуємо теплоту процесу:

Q = 573 K (7,89 - 6,29) кДж/(кг^.К) = 916,8 кДж/кг

Для забезпечення заданої потужності теплообмінника з к.к.д. η = 0,6 необхідно підтримувати витрату пари, що дорівнює

m_t = Ф / Q ^. η = 250 / 916,8 ^. 0,6 = 0,454 кг/с

що складає 1634,4 кг/г або, приблизно, 1650 кг/г.

Приклад.

Дівінил одержують з бутану дегідруванням в адіабатичному реакторі при 7^.10⁵Па. Для підтримки процесу разом з бутаном в реактор подають водяну пару. Визначити витрату пари на 1 кг бутану, якщо на перетворення 1 кг його з 20% виходом дівінила потрібно у вказаних умовах 1100 кДж. Температура реагуючої суміші на вході в реактор 665 °С, а на виході 640 °С.

Рішення.

Спочатку визначаємо, скільки теплоти може повідомити 1 кг водяної пари у вказаних умовах.

Допускаючи, що вміст бутану в реагуючій суміші малий і їм можна нехтувати, вважаємо парціальний тиск водяної пари рівним 7^.10⁵ Па і знаходимо на Н—S-діаграмі крапку, що зображає початковий стан пари. Вона розташована на перетині ізобари 7^.10⁵ Па, з ізотермою 665°С.

Знаючи, що в реакторі Р = const і пара зазнає ізобаричне охолоджування, знаходимо на діаграмі крапку, що зображає кінцевий стан пари. Вона розташована на перетині ізобари, що проходить через початкову точку, з ізотермою 640°С.

Проектуючи знайдені крапки на вісь Н, визначаємо значення ентальпії пари на початку і кінці процесу: h₁ = 3850 і h₂ = 3794 кДж/кг.

Теплота ізобаричного процесу рівна зміні ентальпії: Q = h₂ - h₁ = 3794 - 3850 = —56 кДж/кг

Це означає, що кожен кілограм водяної пари за умов, вказаних в завданні, передає реагуючому бутану (тобто втрачає) 56 кДж.

Звідси знаходимо, що для перетворення 1 кг бутану необхідно:

1100 кДж/кг : 56 кДж/кг = 19,64 кг/кг, тобто приблизно 20 кг пари.

Рисунок - Н — S-діаграма водяної пари.

Питання самоконтролю

1 Зобразіть основні термодинамічні процеси ідеального газу на діаграмі в координатах:

а) Р—V; б) Р—Т; в) V—Т; г) Т—S; д) U—S; е) Н—S.

2 Зобразіть прикордонні криві води на діаграмі в координатах: а) Т—V; б) Р—Т.

3 Зобразіть цикл Карно на діаграмі в координатах: а) Т— V; б) Р—Т; в) Р—S; г) V—S.

4 Як виглядатимуть графіки основних термодинамічних процесів ідеального газу на діаграмі в координатах: а) Р—S; б) V—S.

5 Ступінь сухості вологої пари може приймати значення від 1 до 0. Які значення може приймати ступінь сухості перегрітої пари?

6 При постійному тиску вологу пару доводять до стану перегрітої пари. Опишіть, як при цьому змінюються густина пари, її температура, зовнішній вигляд.

7 Чим відрізняється волога пара від вологого повітря?