
- •Підсилювачі на польових транзисторах
- •Схеми та режими
- •Коефіцієнт підсилення
- •Частотна характеристика
- •Частотна характеристика в області високих частот
- •Частотна характеристика в області низьких частот
- •Загальний вигляд частотної характеристики каскаду
- •Проходження через підсилювач прямокутного імпульсу.
- •Корекція частотних характеристик
- •Нелінійні спотворення
-
Проходження через підсилювач прямокутного імпульсу.
Перехідні процеси у підсилювачі.
Як саме нерівномірність частотної характеристики відіб’ється на формі сигналу, можна проілюструвати на прикладі періодичного прямокутного імпульсу, що проходить через підсилювач. Для цього треба розкласти прямокутний імпульс на гармонічні частотні складові, врахувати всі ті зміни амплітуди та фази, які ці складові зазнають, проходячи через підсилювач, а потім знову їх скласти. Одначе такий шлях є складним і громіздким, тому ми скористаємося іншим, більш простим і наочним методом, заснованим на розгляді перехідних процесів, які відбуваються при проходженні прямокутного імпульсу через кола нашого підсилювача.
Прямокутний імпульс
величиною
 та тривалістю
та тривалістю
 ,
який поступає на вхід підсилювача в
момент
,
який поступає на вхід підсилювача в
момент
 ,
можна розглядати як суму двох імпульсів
увімкнення
,
можна розглядати як суму двох імпульсів
увімкнення
 ,
зсунутих у часі : першого позитивного,
що починається в момент
,
зсунутих у часі : першого позитивного,
що починається в момент
 ,
та другого. Негативного, що починається
в момент
,
та другого. Негативного, що починається
в момент
 (рис.2.14а)2).
Після проходження через вхідне
(рис.2.14а)2).
Після проходження через вхідне
 - коло, яке являє собою диференцюючий
елемент зі сталою часу
- коло, яке являє собою диференцюючий
елемент зі сталою часу
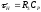 ,
перший импульс увімкнення перетворюється
на експоненціальний імпульс
,
перший импульс увімкнення перетворюється
на експоненціальний імпульс
 (2.13)
(2.13)
Аналогічно, другий імпульс увімкнення створить на затворі транзистора сигнал
 (2.14)
(2.14)
|
|
Їх сума являтиме собою спотворений прямокутний імпульс з різкими фронтами, із скошеню (або, як то кажуть «сколотою») верхівкою і тривалим від’ємним «хвостом» (рис.2.14б). Вихідний сигнал повторюватиме цю форму, будучи, однак, підсиленим за величиною та оберненим за знаком (рис.2.14в). Скол
верхівки та від’ємний хвіст будуть
мало помітні, якщо
|
нерівність еквівалентна
умові
 ,
при якій всі частотні складові сигналу
виявляються значно вищими нижньої
граничної частоти
,
при якій всі частотні складові сигналу
виявляються значно вищими нижньої
граничної частоти
 .
При цьому сигнал не повинний зазнавати
спотворень, що і видно на рис. 2.15а.
.
При цьому сигнал не повинний зазнавати
спотворень, що і видно на рис. 2.15а.
|
|
Якщо
ж
|
|
|
|
Джерелом
спотворень в області високих частот
є вихідне
|
|
У такому вигляді
вихідне коло підсилювача виявляється
зведеним до інтегруючого елемента зі
сталою часу
 .
.
|
|
Уявимо, як і
раніш, вхідний прямокутний імпульс у
вигляді двох зсунутих у часі імпульсів
увімкнення. Кожному з них на виході
підсилювача відповідатиме імпульс
напруги
Аналогічний
вигляд (але зсунутий у часі на
|
При
 перехідний процес зарядки паразитної
ємності через опір
перехідний процес зарядки паразитної
ємності через опір
 закінчується за час, значно менший від
закінчується за час, значно менший від
 (рис.2.17б), так що вихідна напруга
залишається майже незмінною протягом
усього імпульсу, і спотворення його
форми буде майже непомітним. Саме це
відповідає випадку
(рис.2.17б), так що вихідна напруга
залишається майже незмінною протягом
усього імпульсу, і спотворення його
форми буде майже непомітним. Саме це
відповідає випадку
 ,
коли не повинно бути частотних спотворень.
,
коли не повинно бути частотних спотворень.
Якщо ж
 ,
то перехідний процес затягується на
весь час існування імпульсу (рис.2.17в).
Вихідна напруга повільно знижуватиметься
протягом всього імпульсу і таким же
темпом відновлятиметься після його
закінчення. Вихідний імпульс матиме не
прямокутну, а скоріше трикутну форму -
результат його інтегрування вихідним
,
то перехідний процес затягується на
весь час існування імпульсу (рис.2.17в).
Вихідна напруга повільно знижуватиметься
протягом всього імпульсу і таким же
темпом відновлятиметься після його
закінчення. Вихідний імпульс матиме не
прямокутну, а скоріше трикутну форму -
результат його інтегрування вихідним
 - колом підсилювача. Цей випадок
відповідає умові
- колом підсилювача. Цей випадок
відповідає умові
 ,
тобто випадку, коли частоти всіх
гармонічних складових сигналу лежать
вище верхньої граничної частоти
підсилювача.
,
тобто випадку, коли частоти всіх
гармонічних складових сигналу лежать
вище верхньої граничної частоти
підсилювача.


 ,
оскільки напруга на затворі не встигає
істотно змінитися за час імпульсу,
Взявши до уваги, що T
обернено
пропорційне
,
оскільки напруга на затворі не встигає
істотно змінитися за час імпульсу,
Взявши до уваги, що T
обернено
пропорційне
 - першій гармоніці нашого імпульсу, а
- першій гармоніці нашого імпульсу, а
 ,
дійдемо висновку, що вказана вище
,
дійдемо висновку, що вказана вище

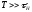 ,
то перехідний процес від переднього
фронту імпульсу закінчиться раніше,
ніж сам імпульс дійде до кінця
(рис.2.15б). Отже, замість прямокутного
імпульсу одержимо гострі викиди -
позитивний від переднього фронту та
негативний від заднього. Обидва викиди
є результатом диференціювання вхідного
сигналу. Нерівність
,
то перехідний процес від переднього
фронту імпульсу закінчиться раніше,
ніж сам імпульс дійде до кінця
(рис.2.15б). Отже, замість прямокутного
імпульсу одержимо гострі викиди -
позитивний від переднього фронту та
негативний від заднього. Обидва викиди
є результатом диференціювання вхідного
сигналу. Нерівність
 еквівалентна нерівності
еквівалентна нерівності
 ,
при якій нижні гармоніки сигналу
опиняються поза межами смуги пропускання
і придушуються, а верхні. що залишилися,
утворюють вельми спотворену картину.
,
при якій нижні гармоніки сигналу
опиняються поза межами смуги пропускання
і придушуються, а верхні. що залишилися,
утворюють вельми спотворену картину.

 - коло, яке складається з навантажувального
опору
- коло, яке складається з навантажувального
опору
 та паразитної ємності
та паразитної ємності
 (рис.2.16а). Для зручності аналізу це
(рис.2.16а). Для зручності аналізу це
 - коло можна зобразити у вигляді
еквівалентного генератора напруги
- коло можна зобразити у вигляді
еквівалентного генератора напруги
 з внутрішнім опором
з внутрішнім опором ,
навантаженого на паразитну ємність
,
навантаженого на паразитну ємність
 (рис.2.16б)3).
(рис.2.16б)3).
 підсилений в
підсилений в
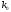 разів за величиною та інвертований
за полярністю. Перехідний процес, який
відповідатиме першому фронту імпульсу
може бути представлений у вигляді:
разів за величиною та інвертований
за полярністю. Перехідний процес, який
відповідатиме першому фронту імпульсу
може бути представлений у вигляді: (2.15)
(2.15) і протилежний за знаком), має і перехідний
процес від заднього фронту імпульсу.
В результаті вихідний сигнал набуває
вигляду імпульсу з пологим переднім
фронтом та затягнутим заднім (рис.2.17а).
і протилежний за знаком), має і перехідний
процес від заднього фронту імпульсу.
В результаті вихідний сигнал набуває
вигляду імпульсу з пологим переднім
фронтом та затягнутим заднім (рис.2.17а).